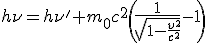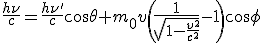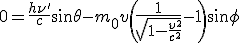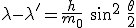Calcul diffusion Compton et Zitterbewegung

De Quantic.

Après s'être cogné partout suite à une hypothèse erronée, Bernard Schaeffer avait presque tout effacé sa page privée, ne laissant que ce bref calcul emprunté au premier tome du Wolfgang Greiner, Quantum Mechanics, an Introduction :

Sommaire

[masquer]

Calcul relativiste d'après "Mécanique quantique" de Greiner p 3

Conservation de l'énergie:

$h\nu= h\nu' + m_0c^2\left( \frac{1}{\sqr{1-\frac{v^2}{c^2}} }$

Conservation de la quantité de mouvement selon l'axe du photon incident:

$\frac{h\nu}{c}=\frac{h\nu'}{c}cos\theta + m_0v\left($

et selon l'axe perpendiculaire où la quantité de mouvement est nulle

$0=\frac{h\nu'}{c}sin\theta- m_0v\left($

En résolvant ces équations, on obtient

$\lambda -\lambda'=\frac{h}{m_0\c}\ sin^2\ \frac{\theta}{2}$

...

On la refait, mais cette fois dans le repère du centre d'inertie, même s'il est expérimentalement irréalisable d'expérimenter dans ce repère, dont l'occurrence est aléatoire : on ne choisit pas à l'avance l'angle de diffusion, on reste prisonniers du repère du laboratoire.

Dans le repère du centre d'inertie

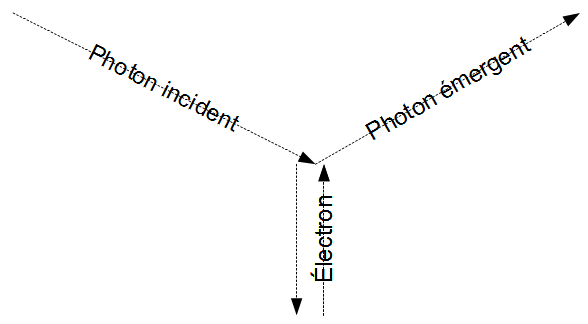
Stuation Compton de base

Là les calculs se simplifient puisque le photon ne change ni de fréquence ni d'énergie, juste de direction. Fixons qu'il arrive de la gauche, en descendant d'un angle 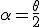$\alpha = \frac{\theta}{2}$ , et continue en remontant du même angle. L'électron ne change pas d'énergie, mais juste de sens de la vitesse. On néglige l'énergie de liaison initiale de l'électron au solide.

Impulsion selon z'z transmise par le photon à l'électron : - 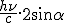$\frac{h\nu}{c}.2\sin\alpha$ (signe - : descendante si l'axe z'z est vertical montant).

Equilibrée par le changement de celle de l'électron : 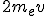2m_ev (premier calcul non relativiste)

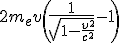$2m_ev\left( \frac{1}{\sqr{1-\frac{v^2}{c^2}} } -1\right)$ forme relativiste.

D'où la vitesse d'arrivée et de fuite de l'électron : 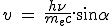$v \hspace{4}=\hspace{4} \frac{h\nu}{m_ec}.\sin\alpha$ (premier calcul non relativiste)

On en déduit sa vitesse de phase : 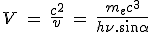$V \hspace{4}=\hspace{4} \frac{c^2} v \hspace{4}=\hspace{4}$

Or on connaît bien la période intrinsèque de l'électron, 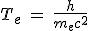$T_e \hspace{4}=\hspace{4} \frac{h}{m_ec^2}$

D'où sa longueur d'onde broglienne : 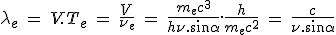$\lambda_e \hspace{4}=\hspace{4} V.T_e \hspace{4} = \hspace{4}$

On remarque que cette longueur d'onde ne dépend pas du tout de la masse de l'électron, et serait la même pour toute autre particule (chargée ou même pas chargée) sujette à diffusion Compton. Elle ne dépend pas non plus de la constante de Planck. Elle ne dépend que l'angle de déviation du photon, et de sa période ou de sa longueur d'onde avant et après la diffusion.

Guidés par ce que nous savons déjà faire en réfraction et réflexion sur un dioptre, il nous faut calculer l'émission du miroir à photon, qu'a constitué cet électron.
La partie horizontale, selon l'axe x'x, est invariante. Sa longueur d'onde est 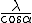$\frac{\lambda}{\cos\alpha}$
La longueur d'onde de la partie pénétrante, et aussi bien de la partie réfléchie du photon est 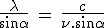$\frac{\lambda}{\sin\alpha} \hspace{4}=\hspace{4}$

Ces deux longueurs d'onde, celle de l'électron rebondissant, et de la partie réfléchie du photon, sont égales.

Il ne reste plus qu'à choisir entre les deux énoncés :
"La diffusion Compton prouve le caractère corpusculaire du photon", ou
"La diffusion Compton prouve le caractère ondulatoire de l'électron".

Or il n'y a pas à tortiller, cette émission de photon partiel montant, et absorption de photon partiel descendant, est bien due à l'accélération de l'électron selon z.

Jusqu'ici, le calcul n'a pas pu donner l'ordre de grandeur des extensions spatiales du photon X et de l'électron. On sait juste, pour avoir assez utilisé la raie $K\alpha$ du molybdène en radiocristallographie des métaux, que sa longueur d'onde est comparable avec les distances interatomiques dans les métaux, et que les électrons de la liaison métallique sont peu liés, et surtout peu localisés, s'étendant sur une à plusieurs dizaines de distances interatomiques. Cela joint aux exigences géométriques de la diffraction sur des plans interatomiques, amène à conclure que le photon et l'électron sont tous deux larges et profonds de quelques dizaines de distances interatomiques tout au long de leur interaction Compton.

Application numérique pour la raie $K\alpha$ moyenne du molybdène :

Prenons un cas de forte déviation du photon, deux fois 30°, soit 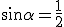$\sin\alpha = \frac 1 2$

La longueur d'onde moyenne de la raie incidente est 0,070926 nm

D'où la projection anti-intérieure sur la direction de propagation de l'électron : 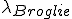$\lambda _{Broglie}$ = 0,070926 nm x 2 = 0,141852 nm.

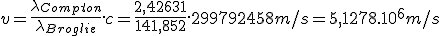
D'où l'on tire la vitesse de l'électron : $v = \frac{\lambda _{Compton}}{\lambda _{Broglie}}.c = \frac$

Soit une vitesse non relativiste, 1,7% de c. Et ce serait encore moins relativiste aux basses déviations.

Puis passer dans le repère de l'électron entrant...

Puis passer dans le repère de l'électron entrant, qui sera assimilé à celui du labo, et l'on devrait retrouver les formules expérimentales d'Arthur Compton.

Avec toutefois les sources d'erreurs suivantes :

Un électron de valence n'est pas au repos, mais au niveau de Fermi, et à la vitesse de Fermi dans le métal.
Et le procédé de calcul a négligé son énergie de liaison, métallique.

C'est le n° 1, le niveau de Fermi, la source la plus grosse d'élargissement des raies Compton, en plus du fait que la raie X $K\alpha$ est un doublet.

Et l'objection de principe qu'on a juste constaté l'échange des vecteurs d'onde, sans faire la physique de l'interaction

Composante verticale du vecteur d'onde gamma entrant = vecteur d'onde électronique sortante.

Composante verticale du vecteur d'onde gamma sortant = vecteur d'onde électronique entrante.

Mais la physique de l'interaction nous échappe encore.

L'échec est garanti si l'on tente d'étendre à ce domaine la modélisation en objet massif qui ralentit, puis repart dans l'autre sens, avec une accélération moyenne finie durant le temps de l'interaction. En 1926 Erwin Schrödinger nous avait montré le chemin en montrant que l'émission d'un photon est le résultat du battement d'une onde électronique entre son état final et son état initial. Ici aussi, il faut faire battre entre eux l'état initial "montant" et l'état final "descendant" (selon le sens choisi pour la figure). Durant ce battement, un état intermédiaire contient une onde broglienne stationnaire.

Il apparaît une autre contrainte, dont nous ne savons pas si elle a été expérimentalement vérifiée : la polarisation électrique est nécessairement dans le plan de la figure.

Condition de Bragg et Zitterbewegung

Rappelons la condition de Bragg en radiocristallographie :

Si d est la distance interréticulaire, 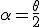$\alpha = \frac{\theta}{2}$ est l'angle du rayon incident sur le plan réticulaire, ou moitié de l'angle de déviation totale, 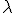$\lambda$ la longueur d'onde du rayonnement incident, et n un entier, ordre de la réflexion :

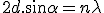
$2d. \sin\alpha = n\lambda$

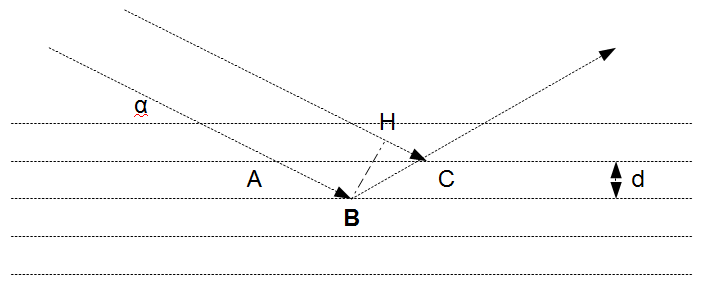
Réflexion en conditions de Bragg

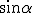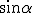
Preuve : arrivant sous l'angle α sur les plans réticulaires AB etc., l'onde monochromatique réfléchie par le plan suivant présente une différence de marche égale à BC - HC. La première réflexion n'existe que si BC - HC vaut exactement une longueur d'onde. Dans le triangle isocèle ABC, d = AB $\sin\alpha$ = BC $\sin\alpha$
Tandis que dans le triangle rectangle BCH, CH = BC 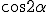$\cos2\alpha$ .
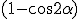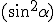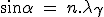
La différence de marche entre les deux ondes est BC - CH = BC $(1 -\cos2\alpha)$ = 2 BC . $(\sin^2\alpha)$ = 2 d $\sin\alpha \hspace{4}=\hspace{4} n.\lambda_{\gamma}$

Or la longueur d'onde broglienne calculée ci-dessus ne nous donne que la réflexion d'ordre deux : 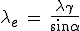$\lambda_e \hspace{4}=\hspace{4}$ .

Une réflexion de faible intensité, tandis que devrait apparaître à l'expérience l'autre réflexion, d'ordre 1, forte, qui n'est jamais observée...

Bon sang ! Mais c'est bien sûr ! C'est l'onde électromagnétique stationnaire à fréquence temporelle et à fréquence spatiale doublée, le Zitterbewegung, ou Tremblement de Schrödinger conforme à l'équation de Dirac, qui donne la bonne équidistance réticulaire de Bragg, exactement d !

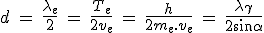
equidistance Compton_Bragg

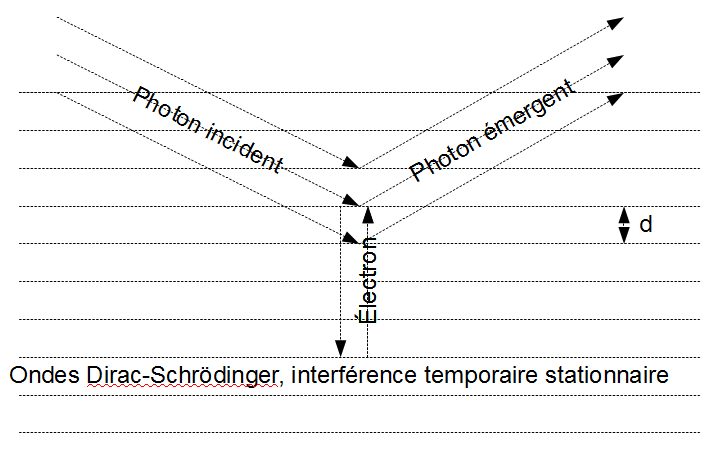
Diffusion Bragg-Compton

Quod Erat Demonstrandum !

C'est bien la fréquence spatiale du Tremblement de Schrödinger, stationnaire durant la réflexion de l'électron sur le photon, qui satisfait à la condition de Bragg pour un réflexe au premier ordre, donnant exactement la diffusion Compton du photon incident.

On se proposait de mettre en évidence le mécanisme physique et ondulatoire qui rendrait compte de la diffusion Compton. Mission accomplie : c'est l'équidistance des ondes temporairement stationnaires de Dirac-Schrödinger qui satisfait à la condition de Bragg, pour la diffusion au premier ordre.

Preuve est faite que la diffusion Compton d'un photon X ou gamma par un électron, est un mécanisme 100% ondulatoire, 0% corpusculaire. Et de plus cela ne s'explique que dans le cadre relativiste postulé par Louis-Victor de Broglie en 1924, avec l'équation finale de Dirac (1928).

Bibliographie et références

E. Schrödinger. Über den Comptoneffect. Annalen der Physik. IV. Folge, 62. http://www.apocalyptism.ru/Compton-Schrodinger.htm

J. Strnad. The Compton effect — Schödinger's treatment. Eur. J. Phys. 7 (1986). http://www.apocalyptism.ru/Compton-effect.htm

Adresses signalés par : Lev Lvovitch Regelson. Compton effect: Schrödinger's treatment in : The Science Forum - Scientific Discussion and Debate. http://www.thescienceforum.com/viewtopic.php?p=235655

P.A.M. Dirac. The Principles of Quantum Mechanics. Oxford University Press, ed 1958.

W. Greiner. Relativistic Quantum Mechanics ; Wave Equations. Springer 1997.

Récupérée de « http://deonto-ethics.org/mediawiki/index.php?title=Calcul_diffusion_Compton_et_Zitterbewegung »