The Zitterbewegung : key of the electron-photon scattering under the laws of Bragg and Compton.

Jacques Lavau
jacques.lavau(at)free.fr

Résumé

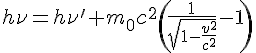
En 1927, Erwin Schrödinger avait présumé prouver que la diffusion d'un photon gamma ou X par un électron étudiée par A. H. Compton, relevait de la loi de Bragg, par interférences sur les réseau d'ondes brogliennes. Toutefois cette démonstration était prématurée et est erronée : seul le réseau d'ondes temporairement stationnaires dans le repère du centre d'inertie, résultant du battement entre les ondes Dirac-Schrödinger (= Zitterbewegung) de l'aller et du retour de l'électron, donne la bonne équidistance requise par la loi de Bragg. L'équidistance Bragg-Schrödinger est électromagnétique (Dirac 1930 -1957, Schrödinger 1930).

Les conditions de Bragg impliquent une largeur et une profondeur de l'ordre de la douzaine de distances interatomiques pour la largeur et la profondeur de l'interaction entre électron et photon. C'est incompatible avec le mythe des "aspects corpusculaires", mythe pourtant hégémonique à ce jour.

Abstract

In 1927, Erwin Schrödinger presumed to have shown that the Compton scattering between an electron and a X photon, is relevant of the Bragg law, computed in the frame of the center of inertia. However, his demonstration could not use in 1927 the right equidistance for the Bragg law. Only the Dirac-Schrödinger electromagnetic waves, whose spatial and temporal frequencies are the double of the Broglian (spinorial) ones, provide the right equidistance for the Bragg law. The lattice of electromagnetic planes that reflect the photon, results of the superposition of incoming and departing electronic waves (Dirac 1930 -1957, Schrödinger 1930).

The Bragg conditions imply about a dozen of interatomic distances for both the depth and the width of the interacting photon and electron. So once again, there are no "corpuscular aspects" in the real physical world. Only waves, emitters and absorbers.

Required

In the frame of the laboratory, the results are well known (Greiner 1981) :

Conservation of the energy :

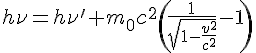
$LaTeX: h\nu= h\nu' + m_0c^2\left( \frac{1}{\sqr{1-\frac{v^2}{c^2}} } -1\right)$

Conservation of the linear momentum on axis of the incident photon :

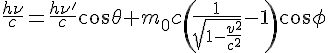
$LaTeX: \frac{h\nu}{c}=\frac{h\nu'}{c}cos\theta + m_0v\left( \frac{1}{\sqr{1-\frac{v^2}{c^2}} } -1\right)cos\phi$

and on the perpendicular axis, where the linear momentum is null :

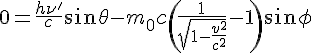
$LaTeX: 0=\frac{h\nu'}{c}sin\theta- m_0v\left( \frac{1}{\sqr{1-\frac{v^2}{c^2}} } -1\right)sin\phi$

Solving these equations, one obtains

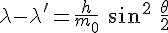
$LaTeX: \lambda -\lambda'=\frac{h}{m_0\c}\ sin^2\ \frac{\theta}{2}$

Demonstration in the frame of the center of inertia

We perform again the calculation, but in the frame of the center of inertia. Of course, one can not experiment in this frame, as its occurrence is at random : one can not choose by advance the scattering deviation, and we remain prisoners of the frame of the laboratory.

There the calculation is far more straightforward and simple : the photon does not change its frequency, nor its energy, only its course. Set it comes from the left, downing by the angle 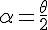$LaTeX: \alpha = \frac{\theta}{2}$ , and then upping by the same angle. The electron does not change of kinetic energy, just the sign of its speed. We neglect its binding energy to the solid.

Momentum on z'z transmitted by the photon to the electron : - 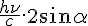$LaTeX: \frac{h\nu}{c}.2\sin\alpha$ (sign - : descending if axis z'z is vertical and upping).

Balanced by the change of momentum of the electron : 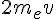LaTeX: 2m_ev (first calculation, non relativistic), or

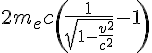$http://www.forkosh.com/mimetex.cgi?2m_e%20c%5Cleft%28%20%5Cfrac%7B1%7D%7B%5Csqr%7B1-%5Cfrac%7Bv%5E2%7D%7Bc%5E2%7D%7D%20%7D%20-1%5Cright%29$ relativistic form.

Hence the speed of incoming and outcoming of the electron : 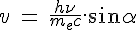$LaTeX: v \hspace{4}=\hspace{4} \frac{h\nu}{m_ec}.\sin\alpha$ (non relativistic)

Hence its phase celerity : $LaTeX: V \hspace{4}=\hspace{4} \frac{c^2} v \hspace{4}=\hspace{4} \frac{m_ec^3}{h\nu.\sin\alpha}$

Now we know the intrinsic period of the electron, 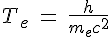$LaTeX: T_e \hspace{4}=\hspace{4} \frac{h}{m_ec^2}$

Hence its broglian wavelength : 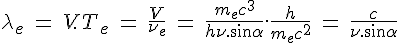$LaTeX: \lambda_e \hspace{4}=\hspace{4} V.T_e \hspace{4} = \hspace{4} \frac{V}{\nu_e} \hspace{4} = \hspace{4} \frac{m_ec^3}{h\nu.\sin\alpha}.{\frac{h}{m_ec^2} \hspace{4}=\hspace{4} \frac{c}{\nu.\sin\alpha}$

It is noteworthy that this wavelength does not depend on the electron mass, and would be the same for any particle, charged or not, which is subject to Compton scattering. It does not depend either of the Planck's constant. It depends only of the angle of deviation of the photon, and of its period or wavelength (evaluated in the frame of the center of inertia) before and after the scattering.

On the model of refraction and reflection on a dioptre, we calculate the emission of this mirror for photon, which is this electron.

The horizontal part, on x'x is unvarying. Its wavelength is 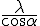$LaTeX: \frac{\lambda}{\cos\alpha}$
The wavelength of the penetrating part, as well of the reflected part of the photon is 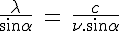$LaTeX: \frac{\lambda}{\sin\alpha} \hspace{4}=\hspace{4} \frac{c}{\nu.\sin\alph$

These two wavelengths, of the rebouncing electron, and of the reflected part of the photon, are equal.

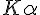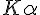Up to now, the calculus has not given anything on the spatial extension of the X photon and electron. We only know, by practice of radiocrystallography with molybdenum $LaTeX: K\alpha$ ray in metallurgy (and copper and cobalt $LaTeX: K\alpha$ in mineralogy), that its wavelength is about the interatomic distances in metals, and that the valency electrons are weakly bound, and little localized, extending on ten or twenty interatomic distances (and the phonons are even less localized). Together with geometric constraints on diffraction on the atomic planes, this compels us to conclude that both the electron and the photon are large and deep of tens of interatomic distances, all along the Compton interaction.

Numerical calculus, with the mean $LaTeX: K\alpha$ ray of molybdenum :

Let us take a case of strong deviation of the photon, twice 30°, that is 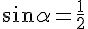$LaTeX: \sin\alpha = \frac 1 2$

The mean wavelength of incident ray is 0.070926 nm

Hence the external projection (external to the propagation of the electron) : 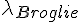$LaTeX: \lambda _{Broglie}$ = 0,070926 nm x 2 = 0,141852 nm.

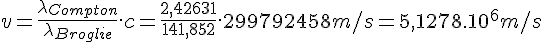
Hence the speed of the electron : $LaTeX: v = \frac{\lambda _{Compton}}{\lambda _{Broglie}}.c = \frac {2,42631}{141,852}. 299792458 m/s = 5,1278 . 10 ^6 m/s$

It is an non-relativistic speed : 1.7% of c. It would even less relativistic with low deviations.

Then to the frame of the incoming electron...

Passing to the frame of the incoming electron, not very different from the frame of the laboratory, one should retrieve the experimental formula of Arthur Compton. However with the following causes of error :

A valency electron is not at rest, but at Fermi level and Fermi speed in the metal.
And we have neglected its binding energy, in metallic binding.

The first mentioned is the main cause of error and enlarging of the Compton scattering, the Fermi Level, plus the fact that the 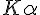$LaTeX: K\alpha$ X ray is a doublet.

The principle objection is that we have just stated the exchange in wave vectors, without establishing the physics of the interaction

Vertical component of the gamma incoming wave vector = electronic wave vector outcoming.

Vertical component of the gamma outcoming wave vector = electronic wave vector incoming.

So the physics of the interaction remains unknown at this step of the calculus.

The failure is guaranteed if we extrapolate to microphysics the usual macrophysical scheme, with a massive object that slows, then restarts in the opposite direction, with finite acceleration all during the interaction. In 1926 (Schrödinger 1926) Erwin Schrödinger had showed the path, considering emission of a photon as the beat of atomic (or molecular) electronic wave between its final and initial state. Here again, it is a matter of beating between the initial upping state and final downing state of the electron. During the beating, an intermediate state contains a stationary broglian wave, to dispatch among four Dirac's components, whose two are antichrones, with negative frequencies.

Here is obvious another constraint, but we do not know whether it has been experimentally proved (nor whether it can be experimentally tested) : the electrical polarization is necessarily in the plane of the drawing.

Bragg's condition and Zitterbewegung

The Bragg condition in radiocrystallography :

Set d is the interreticular distance, 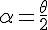$LaTeX: \alpha = \frac{\theta}{2}$ is the angle of the incident ray on the reticular plane, or half of the total deviation, 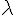$LaTeX: \lambda$ the wavelength of the incident ray, and n an integer, order of the reflection :

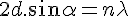
$LaTeX: 2d. \sin\alpha = n\lambda$

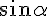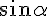
Demonstration : incoming with α on the reticular planes AB etc., the monochromatic wave reflected by the next plane has a path difference equal to BC - HC. The first reflexion only exists if BC - HC is exactly one wavelength. In the isosceles triangle ABC, d = AB $LaTeX: \sin\alpha$ = BC $LaTeX: \sin\alpha$
Though in the rectangular triangle BCH, CH = BC 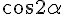$LaTeX: \cos2\alpha$ .
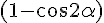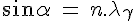
The path difference between the two waves is BC - CH = BC $LaTeX: (1 -\cos2\alpha)$ = 2 BC . $LaTeX: (\sin^2\alpha)$ = 2 d $LaTeX: \sin\alpha \hspace{4}=\hspace{4} n.\lambda_{\gamma}$

Nevertheless, the broglian wavelength, as calculated above, which was the only known and used by Erwin Schrödinger in 1927 (Schrödinger 1927) only gives us the reflection of second order : 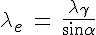$LaTeX: \lambda_e \hspace{4}=\hspace{4} \frac{\lambda_{\gamma}}{\sin\alpha}$ .
Its is a weak reflection, though one should observe the main reflection at order 1, which is never observed (and which would violate the laws of conservation of energy-momentum)...

It remains only one outlet : to consider the stationary electromagnetic wave, with doubled temporal and spatial frequencies, the Zitterbewegung, the trembling motion discovered by Erwin Schödinger in 1930 (Schrödinger 1930, Dirac 1930, 1958) according to the Dirac equation, which yields the right Bragg reticular equidistance, exactly d !

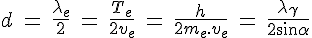
$LaTeX: d \hspace{4}= \hspace{4} \frac {\lambda_e}2 \hspace{4}= \hspace{4} \frac{T_e}{2 v_e} \hspace{4}= \hspace{4} \frac{h}{2 m_e.v_e} \hspace{4} = \hspace{4} \frac{\lambda_{\gamma}}{2\sin\alpha}$

Quod Erat Demonstrandum !

Conclusions

Only the spatial frequency of the Zitterbewegung, the trembling motion discovered by Erwin Schrödinger in 1930, stationary during the reflection of the electron on the photon, satisfies the Bragg condition for a first order reflex, and gives exactly the Compton scattering of the incoming photon.

Our aim was to exhibit the physical and undulatory mechanism that lies under the Compton scattering. Goal accomplished : Only the equidistance of the temporarily stationary Dirac-Schrödinger waves satisfies the Bragg condition, for first order diffraction. The fact that Erwin Schrödinger did not correct himself in 1930 his error of 1927, gives the measure of the meticulous demoralization obtained on him by Bohr and Heisenberg (Segrè 1984, Selleri 1986). Not the slightest allusion on that in his Nobel lecture in 1933, where the two last pages deny all the work described in the previous pages.

Other consequences :

Knowing the spatial extent of a conduction electron at the Fermi level, the Compton interaction electron-photon only imposes to this apex a modest constraint of pinching of the Fermat's taperings, about some nanometers, when the reactional conditions on the previous emitter and following absorber, as well for the electron and the X photon can eventually be more pinched ; the details depend on the precise physics of these emitters and absorbers.

The electron returns under physical laws, individually. Well, it may sound a dullness, however under the standard mythology (Greiner 1935, Charpak, Omnès 2004, Hawking, Mlodinow 2010), each quanton individually escaped to any physical laws. Only in great numbers, it rejoined statistically some physical laws, by the mysterious mean of a physical mechanism remaining totally mysterious, though postulated however.

It is no more necessary to postulate some exorbitant physical mechanism, never observed and never theorized, that could perform the magic transmutation of an electron or a photon into some "small corpuscle", or worse : "punctual corpuscle".

Thanks

Thanks to Lev Lvovitch Regelson, who accomplished an unprecedented act of withstand : let accessible to all a paper from Erwin Schrödinger, at http://www.apocalyptism.ru/Compton-Schrodinger.htm

Bibliography and references

Compton 1923 : Arthur H. Compton. A quantum theory of the scattering of X-rays by light elements. The Physical Review. May 1923, vol 21, n°5.

P.A.M. Dirac. The Principles of Quantum Mechanics. Oxford University Press, ed 1958. § 69.

Greiner 1981 : W. Greiner. Relativistic Quantum Mechanics ; Wave Equations. Springer Verlag, ed. 1997.

Schrödinger 1926 : An Undulatory Theory of the Mechanics of Atoms and Molecules. The Physical Review, 28, (1926), 1049-1070

Schrödinger 1927 : E. Schrödinger. Über den Comptoneffect. Annalen der Physik. IV. Folge, 62. http://www.apocalyptism.ru/Compton-Schrodinger.htm
Adresses given by : Lev Lvovitch Regelson. Compton effect: Schrödinger's treatment in : The Science Forum - Scientific Discussion and Debate. http://www.thescienceforum.com/viewtopic.php?p=235655 , link changed to : http://www.thescienceforum.com/physics/18025-compton-effect-schroedingers-treatment.html

Schrödinger 1930 : Über die kräftefreie Bewegung in der relativistischen Quantenmechanik. Sitzungsberichte der Preußischen Akademie der Wissenschaften. Physikalisch-mathematische Klasse, (1930), 418-428

Schrödinger 1933 : Nobel Lecture, December 12, 1933. The Fundamental Idea of Wave Mechanics. http://www.nobelprize.org/nobel_prizes/physics/laureates/1933/schrodinger-lecture.html http://www.nobelprize.org/nobel_prizes/physics/laureates/1933/schrodinger-lecture.pdf

Segrè 1984 : Emilio Segrè. Les physiciens modernes et leurs découvertes. Fayard, Paris 1984.

Selleri 1986 : Franco Selleri. Le grand débat de la théorie quantique. Flammarion, Paris 1986.

Anti-references, a bunch of what not to do (collected at : http://citoyens.deontolog.org/index.php/topic,887.0.html ) :

Georges Charpak et Roland Omnès. Soyez savants devenez prophètes. Ed. Odile Jacob, Paris, juillet 2004. Pages 87 - (92 ?).
Wolgang Greiner 1935. Quantum Mechanics, Special Chapters, pp 365-367. Springer Verlag, ed. 1998.
Stephen Hawking, Leonard Mlodinow 2010. The Grand Design. Bentham Books, 2010.