Pour une onde radio (ou UHF transmettant la télévision), observer la polarisation de l’onde est immédiat : il suffit d’orienter l’antenne (fil conducteur, ou bâton conducteur), pour voir la réception s’améliorer jusqu’à son maximum, ou s’éteindre presque complètement. En chaque point, une seule orientation d’antenne est optimale. Cette expérimentation réclame un champ propre et simple. Dans une cour d’immeuble encaissée, on ne reçoit que des réflexions multiples, et aucune orientation n’est ni vraiment bonne, ni vraiment nulle.
On peut expérimenter avec deux “ talkies-walkies ” à bon marché. Si leurs antennes sont parallèles entre elles, et perpendiculaires à la direction de propagation, on a une bonne réception. Antennes croisées, ou parallèles à la propagation : réception presque nulle.
Dessinez ci-dessous la première expérience : l'émetteur tient son antenne verticale. Comment le récepteur doit-il s'orienter ?
Seconde expérience : l'émetteur tient son antenne horizontalement. Dans quelles conditions pourra-t-on le recevoir normalement ?
Les champs électriques, nous nous en servons tous les jours dans nos oscilloscopes. Nous nous en servons aussi dans les électrolyses, dans les tubes fluorescents qui éclairent nos salles. Etc. Nous en avons manipulés lorsqu’on a fait une électrolyse : la cathode a attiré des cations Na+, et l’anode a attiré des anions Cl-. Dans nos oscilloscopes : une anode percée accélère des électrons e-, et les laisse continuer leur course vers l’écran fluorescent. Les plaques de déviation créent un champ électrique qui dévie ces électrons, et leur donnent une déviation proportionnelle à la différence de potentiel entre ces plaques, respectivement horizontales et verticales.
La force exercée sur une charge électrique q, est le produit de cette charge, par le champ électrique :
F = q E.
Et
cette loi est vectorielle :
L’unité de champ électrique est le volt par mètre. D’après la loi ci-dessus, on pourrait aussi dire le : . . .
Cette loi se dessine plus facilement si le corps d'épreuve du champ électrique est une charge positive :
|
|
+ e représente la charge d’un proton. |
Finissez de légender ce dessin : les potentiels les plus positifs, sont-ils à gauche, ou à droite de la figure ?
On dessine donc le champ électrique comme un champ de flèches, qui couleraient des charges +, vers les charges -. Est-ce le même sens que le sens du courant conventionnel ?
Si ce corps d'épreuve est un électron, de charge négative, voici :
|
|
- e représente la charge d’un électron. |
Autrement dit, l'électron négatif, fuit les autres électrons.
Un mot nouveau : corps d'épreuve. C'est le genre d'objet qu'il faut placer dans un champ, pour que la force qui en résultera, trahisse quel est ce champ, ses caractéristiques, sa grandeur, son orientation. Pour le champ de gravitation, n'importe quel objet est un corps d'épreuve : une pomme, un ballon ; ils tombent...
Remarque : tous les corps tombent dans le même sens : vers le centre de la Terre, pour notre voisinage. Alors qu'il y a deux sortes de corps d'épreuve en électromagnétisme ; les charges - et les charges +.
Le champ magnétique a de nombreuses particularités qui nous sont nouvelles. Il n’a aucune des propriétés d’un vecteur. Nous appellerons cela un gyreur. Un champ magnétique, n’est rien d’autre qu’un champ électrique, mais vu à travers un mirage (un mirage de l’espace-temps) : il traduit qu’une charge électrique a une vitesse de déplacement, et il le traduit à la façon d’un chemin à rouleaux, ou d’un roulement à rouleaux.
|
Un champ magnétique, est un être qui tourne et fait tourner une vitesse. Cet être-là est dans un plan : le plan de la rotation. Ce champ magnétique B, traduit le fait : je vois tourner un courant devant moi. Le produit i.l, intensité du courant, par la longueur d’un élément de circuit, est un vecteur. |
|
La force qui dévie un courant, ou un électron lancé, sous l’effet du champ magnétique, est aussi un vecteur. Et le champ magnétique est le quotient de deux vecteurs perpendiculaires. Il ne peut donc en aucun cas être lui-même un vecteur. On l’a parfois appelé un “ bivecteur ”, mais trop de gens confondent avec “ vecteur ”. Nous l'appellerons ici un “ gyreur ”.
|
Son
effet est de faire tourner -
dévier de
sa trajectoire - une charge électrique déjà
en mouvement,
ou autrement dit, d’exercer une force
de
déviation
latérale sur un courant. Un rond dans un rond, et qui tournent pareil ! |
|
Effet d’un champ magnétique sur un électron lancé : il incurve sa trajectoire selon un arc de cercle. Prenons le cas d’un électron lancé, dans un champ uniforme. On étudiera seulement le cas simple, où la vitesse initiale est déjà dans le plan qui contient le champ magnétique.
|
|
Et on observe encore un rond dans un rond, et qui tournent pareil ! Bien sûr, il y a un truc ! J’ai pris comme corps d’épreuve du champ magnétique, des électrons, dont la charge est négative. Si j’avais pris un courant électrique comme corps d’épreuve, son “ rond ” aurait tourné en sens contraire. Nous
verrons les lois quantitatives exactes dans le cours
consacré à
l’électromagnétisme. |
L’unité de champ magnétique est le tesla (de l’ingénieur croate Nikola Tesla, inventeur du moteur synchrone), symbole T. Il est égal à 1 Newton par coulomb, et par m/s.
|
Type de champ |
corps
d’épreuve du champ ? |
quoi produit
le
champ ? |
géométrie |
Potentiel
associé |
|
|
champ de
gravité |
tout corps
matériel. |
Tous les
corps
matériels. |
Vecteur: g |
Scalaire: g.h |
|
|
champ
électrique |
toute charge
électrique |
des charges
électriques. |
Vecteur.
Unité :
V. m-1. |
Scalaire :
Volt, ou
J.Cb-1 |
|
|
champ
magnétique |
toute charge
électrique en mouvement |
des charges
électriques en mouvement, des courants, des aimants. |
gyreur :
Unité :
tesla, ou V. s . m-2. |
Vecteur :
V. s . m-1 (Volt/vitesse). |
|
|
Onde
électromagnétique |
Toute charge
électrique, atomes. |
Tout
changement de
position ou de vitesse d’une charge
électrique. |
gyreur en
dimension 4 : temps + espace. |
Vecteur en
dimension 4 : temps + espace. |
|
|
Champ
nucléaire
(fort) : champ à très courte
distance : juste un noyau atomique. |
protons,
neutrons |
protons,
neutrons |
|
|
|
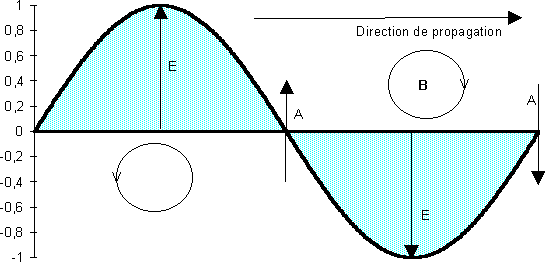
Un
troisième champ, vectoriel, a été
dessiné, 
. Il
est en avance
sur 
d'un
quart de
longueur d'onde. 
est
au maximum quand 
est
nul. 
ressemble
beaucoup à
un courant électrique : 
,
qui précède, est la cause de 
,
qui suit un quart de période plus tard. On
l'appelle :
potentiel magnétique. En termes simplifiés, le
potentiel V traduit qu'il y a
des charges électriques "pas loin". En simplifiant, le
potentiel 
traduit
qu'il y a un
courant électrique "pas loin", et 
a
l'orientation et le
sens du courant le plus proche et le plus fort.
On
constate qu'un électron, soumis au champ
magnétique B,
et au champ électrique 
,
est poussé dans le sens de propagation de l'onde.
Sur la figure page suivante, exerçons-nous à le prouver dans quatre cas :
Pour cela dessinons au crayon la trajectoire sous l'influence du champ électrique, puis dévions la, comme elle est déviée par le champ magnétique.
Constats :
Transversalement, les charges - sont . . .
Transversalement, les charges + sont . . .
Longitudinalement, toutes les charges électriques sont . . .
Pourquoi appelle-t-on une telle onde "onde polarisée plane" ? Pour répondre, cherchez si un même plan contient 2 vecteurs et un gyreur caractéristiques de l'onde : le vecteur de propagation, le vecteur champ électrique, et le gyreur champ magnétique.
Et dans quel plan placerez-vous une antenne yagui, en réception d'onde UHF de télévision ?
En
général, chaque atome
qui émet de la lumière, le fait au hasard, et
dans un plan de polarisation au
hasard par rapport aux autres atomes émetteurs.
Calculons combien de temps
peut durer l'émission (polarisée) d'un seul
atome : environ 10 000 périodes,
à la fréquence de 500 THz :
Une
telle
durée
est-elle
facile à observer ?
Il
faut donc
utiliser des
moyens spéciaux pour observer la polarisation de la
lumière. Au 19e
siècle, on n'avait que deux moyens :
·
Certains
cristaux, comme
la calcite CaCO3
, séparent et
transmettent différemment deux polarisations, selon
l'orientation du cristal
par rapport au rayon lumineux.
·
La
réflexion et
la
réfraction à travers un dioptre, produisent une
polarisation non complète. Mais
plusieurs réfractions ou plusieurs
réflexions en série, peuvent faire une
polarisation très complète.
De nos jours, on utilise de préférence des Polaroïds. Ces feuilles sont des préparations de hauts polymères transparents, dans lesquels sont noyées des molécules organiques conductrices (iodure d'alcool de polyvinyle), et alignées dans une même direction. Elles arrêtent donc le champ électrique dans le sens de leur alignement, et absorbent ainsi une des polarisations, et laissent passer la polarisation perpendiculaire.
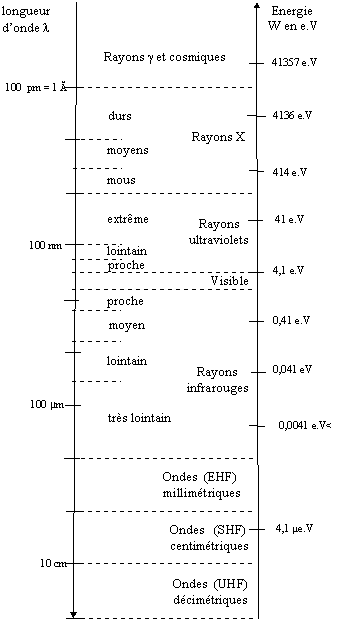
L'ultraviolet fait bronzer la peau, il déclenche des réactions chimiques, il provoque des fluorescences, il provoque des mutations dans les cellules vivantes, il rend conducteur un photoconducteur, etc.
C'est Einstein, en 1905, qui a exprimé la loi : un rayonnement électromagnétique n'interagit avec la matière que par quanta, déterminés par la constante de Planck h. h vaut environ 6,626176 . 10-34 joule-seconde par cycle, ou 1,05457267 . 10-34 joule-seconde par radian.
On a nommé ces quanta "photons". Voici la loi originale d'Einstein :
W = h . f. où f est la fréquence du rayonnement, et W l'énergie que chaque quantum transporte.
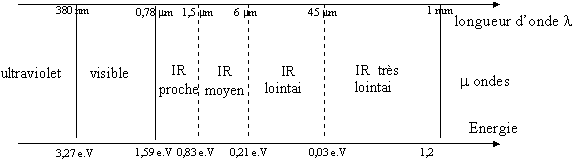
En spectroscopie infrarouge (détection du monoxyde de carbone par sa raie d'absorption à 4,666 µm), nous avons rencontré cette loi sous une forme un peu modifiée par Bohr :
E1 - E2 = h .f, où E1 est l'énergie de la molécule avant absorption d'un quantum de rayonnement, et E2 est l'énergie de la molécule après absorption.
Nous ferions mieux de réécrire cette loi, en écrivant qu'une expression est égale à une constante universelle :
W T = h,
ou
W /
= h
/ 2.Pi
=
.
Avec
désignant
la pulsation, T
désignant la période.
Sur un PC, recherchez quel est le granule d'une disquette : la plus petite unité d'allocation que le système d'exploitation réserve sur un disque, pour un fichier. Ayez une disquette formattée dans le lecteur A :, puis tapez sous DOS :
DIR A: (notez la place disponible : L0)
COPY CON A:ESSAI
AB (ou un autre message bref : celui totalisera 3 signes : AB^Z)
^Z
DIR A: (notez la nouvelle place disponible : L1)
Le granule est la différence L0 - L1. Sur les disquettes double densité, il valait 1 k octets. Sur les disques durs, il n'est jamais inférieur à 2 k. Quelle valeur avez-vous trouvé sur une disquette haute densité ?
Maintenant vous avez une comparaison familière pour cette constante h. C'est le granule d'action (c'est depuis 1834 le nom consacré à cette grandeur, inventée par W. R. Hamilton) de la nature. Ce granule d'action h , ou quantum d’action, régit toute la nature.
Les molécules peuvent tourner sur elles-mêmes, et vibrer, mais exclusivement à des niveaux multiples demi-entiers du quantum d’action h. La molécule de monoxyde de carbone CO vibre en permanence sur le mode élongation-compression. Mais elle ne peut pas descendre en dessous d’un niveau d’énergie de vibration égal à W0 = ½ . 0 (dite énergie de vibration de zéro).
Elle peut sauter à W1 = (1 + ½) . 1, ainsi qu’éventuellement à des degrés supérieurs. Ces pulsations 1 et 0 sont presque égales à celles de la radiation infrarouge absorbée: W1 - W0 = . .
C’est ainsi qu’en spectrométrie infrarouge, on mesure les modes de vibrations des molécules.
Il y a beaucoup d’autres modes d’interaction entre atomes ou molécules, et rayonnement.
En spectrométrie micro-ondes, on mesure leurs modes de rotation. En spectrométrie visible et lutraviolet, on mesure les niveaux d’énergie des électrons périphériques autour des atomes. En spectrométrie X, on mesure les niveaux d’énergie des électrons profonds (premières couches, sur les éléments lourds). En spectrométrie gamma, on mesure la structure du noyau atomique.
C’est
par ces moyens, que l’on peut connaître la
composition
des étoiles: en analysant leur lumière avec des
prismes dispersifs, et de plus
en plus, avec des réseaux.
