Liens entre dimension
physique et caractère tensoriel. Auteur : Jacques Lavau
2. Famille
connexe des grandeurs de la mécanique.
3. Famille
connexe des grandeurs de l'électromagnétisme.
4. Tableau de
chasse; et sa mise en forme.
5. L'action et le
formalisme hamiltonien.
5.1.
Noether et le formalisme canonique.
5.2.
En translation, avec la somme des forces.
6. Conclusion
provisoire en proverbes.
|
Fin de la série
d'articles |
Liens entre dimension physique et
caractère tensoriel.
Auteur : Jacques Lavau
1. Objectifs
Les lois physiques, reliant des grandeurs entre elles, restreignent notre fantaisie. La vie serait simple, s'il suffisait du premier coup d'oeil à la dimension physique d'une grandeur pour trancher de son caractère géométrique. La physique entière n'a pas la simplicité de la seule cinématique. Nous aurons à tenir compte des densités et des capacités, pour tous les phénomènes de volume et de surface. Nous utiliserons le caractère extensif des grandeurs intervenant dans tous les grandes lois de conservation. Nous utiliserons le théorème d'Emmy Noether, et les implications du formalisme canonique.
2. Famille connexe des grandeurs de la mécanique.
C'est incontournable : les lois physiques relient les grandeurs entre elles. Savoir si toutes les grandeurs de la physique sont ainsi rigidement connectées, est un débat difficile. La mécanique est un domaine où la connexion entre grandeurs est simple et peu discutable, surtout dans son formalisme newtonien. Dressons-en les tableaux, cinématique, et dynamique, afin d'en dégager des lois, au moins phénoménologiques :
Cinématique :
|
Lα.T-β |
L-1 |
Angle
: L0 |
Longueur : L1 |
Surface : L2 |
Volume : L3 |
|
pas de temps : T0 |
|
Rotation, déformation |
déplacement |
|
|
|
T-1 |
|
vitesse angulaire |
vitesse |
vitesse aréolaire |
|
|
T-2 |
|
accélération angulaire |
accélération |
|
|
Dynamique :
|
M. Lα.T-β |
L-1 |
L0 |
L1 |
L2 |
L3 |
|
pas de temps : T0 |
|
Masse |
|
moment d'inertie |
|
|
T-1 |
|
|
impulsion |
moment cinétique, et action |
|
|
T-2 |
contrainte, pression |
|
force |
moment d'une force, et énergie. |
|
On a bien quelques régularités remarquables dans ces deux tableaux, mais trop peu, semble-t-il :
Toutes les grandeurs vectorielles sont dans la colonne L1, où la longueur figure à la puissance 1.
Tous les gyreurs (tenseurs de rang 2) sont dans les colonnes L0 et L2.
Mais la déformation d'un solide ou d'un fluide, et sa vitesse de déformation, tenseurs non antisymétriques, occupent aussi la colonne L0. Et un tenseur de rotation n'est que partiellement antisymétrique.
La colonne L2 aussi, fait désordre : elle contient à la fois des gyreurs, et tout autre chose. Autrement dit des produits extérieurs, des produits intérieurs, un produit tensoriel symétrisé (le moment d'inertie).
3. Famille connexe des grandeurs de l'électromagnétisme.
Nous avons à construire nos tableaux, en fonction des unités de base : masse, et charge électrique. On remarque des régularités similaires dans ces deux tableaux :
|
Q. Lα.T-β |
L0 |
L1 |
L2 |
|
T0 |
Charge électrique |
dipôle électrostatique |
|
|
T-1 |
intensité |
élément de courant |
moment magnétique d'un aimant, d'une particule. |
|
M.Q-1. Lα.T-β |
L0 |
L1 |
L2 |
|
T-1 |
champ magnétique |
potentiel vecteur |
flux magnétique |
|
T-2 |
|
Champ électrique |
potentiel électrique |
Toutes les grandeurs vectorielles sont dans la colonne L1, où la longueur figure à la puissance 1.
Toutes les grandeurs gyratorielles sont dans la colonne L0, ou dans la colonne L2. Mais on y trouve aussi un vrai scalaire (la charge électrique), un faux "scalaire" (l'intensité), et un discutable (le potentiel).
Trois relations diagonales, relativistes, sont bien en place, deux vectorielles, et une tensorielle : La charge électrique et l'élément de courant forment bien un vecteur de dimension 4 en espace de Minkowski. Ainsi que le potentiel-vecteur magnétique et le potentiel électrique : vecteur de dimension 4.
Le champ électrique et le champ magnétique forment bien un tenseur antisymétrique de rang deux en dimension 4 : le tenseur dit "de Faraday", ou rotationnel du vecteur-potentiel précédent.
Mais deux grandeurs vectorielles ruent dans le tableau : le
tenseur de Poynting, de dimension [M . T-3], le "courant de
déplacement" 
de Maxwell, de dimension [L-2. Q]; et une
grandeur gyratorielle : 
, de dimension [L-1.T-1. Q]. Formons
alors la conjecture que ce vecteur 
, ce gyreur 
, sont des densités volumiques de quelque chose à préciser :
L3. 
:
[L . Q].
C'est bien la dimension attendue d'un vecteur : déplacement de charges électriques dans un diélectrique.
L3. 
:
[L2 . T-1 . Q].
C'est bien la dimension attendue d'un gyreur : vitesse aréolaire d'une charge électrique autour d'un axe.
Donc au prix de l'introduction des densités vectorielles et gyratorielles, la famille des grandeurs vectorielles retrouve son unité dimensionnelle de principe, de même la famille gyratorielle. Brillouin et Barbotte avaient bien vu le problème, mais hélas, le premier réflexe du physicien (moi aussi, je plaide coupable à ce sujet), est de bazarder ces "subtilités inutiles".
Il ne reste que le problème posé par le tenseur de Poynting, flux de puissance électromagnétique franchissant une unité de surface, de dimension [M . T-3]. En milieu de propagation isotrope, il est sans grand danger de le confondre avec un vecteur. La contradiction éclate, dès que la radiation se propage dans un milieu anisotrope, tel un spath d'Islande, où la propagation est sensible à la polarisation.
De ce faux-vecteur, on déduit la pression de radiation (la contrainte de radiation, en milieu anisotrope) en le divisant par c/2 (dimension [M . L-1 . T-2]) : densité surfacique d'impulsion par unité de temps, en [L-1].
On en déduit aussi la densité volumique de quantité de mouvement transportée par l'onde, en le divisant par c² : dimension [M . L-2 . T-1]. La loi générale des densités volumiques vectorielles, en [L-2], est bien respectée. Les interventions de la constante c (et c²) jouaient à nous égarer - avec un succès certain.
Il est prudent de retenir que les densités et capacités sont, en réalité, de nature tensorielle, et que ce n'est que dans certains cas favorables, qu'on peut sans danger les assimiler à des tenseurs de rang moindre : scalaires, vecteurs, gyreurs.
4. Tableau de chasse; et sa mise en forme.
Rassemblons notre "tableau de chasse" des grandeurs vectorielles, et gyratorielles. Afin d'éviter d'entassser les densités et les capacités avec d'autres grandeurs très différentes, n'oublions pas de dérouler notre tableau, selon la valence brute totale (covariante + contravariante), au lieu de le tasser selon la valence nette.
|
|
L-3 |
L-2 |
L-1 |
L0 |
L1 |
L2 |
L3 |
|
rang zéro |
|
|
|
Scalaire. |
|
|
|
|
rang un |
|
|
Covecteur. Densité linéique de scalaire. |
|
Vecteur. Capacité linéique de scalaire. |
|
|
|
tenseur de rang deux, (bivecteur). |
|
Cogyreur étendu. Densité surfacique de scalaire. |
|
Tourneur strict. Densité linéique de vecteur. |
|
Tourneur étendu. Capacité linéique de vecteur. Capacité surfacique de scalaire. |
|
|
tenseur de rang trois (trivecteur) |
Densité volumiquede scalaire. |
|
Densité surfacique de vecteur. Capacité linéique de cogyreur étendu. |
|
Capacité surfacique de covect. Densité linéique de gyreur étendu. |
|
Capacité volumique de scalaire. |
|
tenseur de rang ou ordre 4. |
|
Densité volumique de vecteur. |
|
Densité surfacique de gyreur étendu. Capacité surfacique cogyreur étendu. |
|
Capacité volumique de covecteur. |
|
|
tenseur de rang ou ordre 5 |
|
|
Densité volumique de gyreur étendu. |
|
Capacité volumique de cogyreur étendu. |
|
|
Ce tableau a une structure manifeste, avec seulement 15 cases remplissables, et suggère que les grandeurs de la physique macroscopique non relativiste répondent à une syntaxe beaucoup plus stricte qu'on n'a pensé à nous l'enseigner.
Or, s'il est une chose que les informaticiens ont appris, à leurs dépens, et fort rudement, c'est combien une stricte syntaxe dans le langage pratiqué, aide à dépister les inévitables erreurs que l'on commet au jour le jour. Faute d'être encadrés par une syntaxe claire et stricte, nombre de physiciens ont publié de fameuses bourdes, que la diplomatie interdit de citer trop précisément.
Pourtant, un examen serré montre que nous n'avons pas atteint une structure explicative tout à fait satisfaisante : que signifient ces rangs ou ordres 4 et 5 ? Nous n'en avons pas donné de définition précise, restant dans le flou heuristique. Utilisons donc les deux valences : (valence contravariante, valence covariante).
|
|
L-3 |
L-2 |
L-1 |
L0 |
L1 |
L2 |
L3 |
|
rang zéro |
|
|
|
(0,0) |
|
|
|
|
rang un |
|
|
(0,1) |
|
(1,0) |
|
|
|
rang 2. |
|
(0,2) |
|
(1,1) |
|
(2,0) |
|
|
rang 3. |
(0,3) |
|
(1,2) |
|
(2,1) |
|
(3,0) |
|
"ordre 4" |
|
(1,3) |
|
(2,2) |
|
(3,1) |
|
|
"ordre 5" |
|
|
(2,3) |
|
(3,2) |
|
|
Nous voyons enfin que dans la dimension Lα, l'indice α. est égal à la valence nette. Nous devrons renoncer à l'espoir que la dimension physique aide à distinguer la symétrie ou l'antisymétrie d'un tenseur; elle ne nous donnera rien de plus que la valence totale nette.
Pour préparer une discussion relativiste, tentons de séparer quelques grandeurs qui seraient elles aussi en Mc², comme l'énergie, et comptons leur dimensionnalité à partir de Mc² au lieu de M :
Dynamique, famille de la masse (grandeurs toutes extensives,
sauf la contrainte) :
|
M. Lα.T-β |
L-1 |
L0 |
L1 |
L2 |
|
T0 |
|
(0,0) Masse |
|
(2,0) moment d'inertie |
|
T-1 |
|
|
(1,0) impulsion |
(2,0) moment cinétique |
|
T-2 |
(1,2) contrainte, pression |
|
(1,0) force |
(2,0) moment d'une force |
Dynamique, famille de l'action (ou peut-être de l'énergie ?)
:
|
Mc². Lα.T-β |
L-3 |
L-2 |
L-1 |
L0 |
|
T1 |
|
|
(0,1) impulsion |
(0,0) action |
|
T0 |
(0,3) contrainte, pression |
|
(0,1) force |
(0,0) énergie |
|
T-1 |
|
(3,1) tenseur de Poynting |
|
|
On aura remarqué l'ambigüité du statut de la force, et peut-être de l'impulsion, qui jouent sur les deux tableaux. De même, le tenseur de contrainte (ou de pression s'il est isotrope) est aussi bien produit d'un vecteur force par un covecteur surface, que densité volumique d'énergie élastique. Du moins à première vue.
Sans doute faut-il accepter ce double-jeu comme inhérent à la nature des choses de la Nature, et non comme artéfact dû à nos habitudes de représentation ?
En électromagnétisme, la famille de la charge électrique ne
présente ni surprise ni irrégularité :
|
Q. Lα.T-β |
L-2 |
L-1 |
L0 |
L1 |
L2 |
|
T0 |
(1,3) : densité de polarisation : |
|
(0,0) : Charge électrique |
(1,0) : dipôle électrostatique |
|
|
T-1 |
(1,3) : densité de courant |
(2,3) : densité de moment magnétique |
intensité d'un courant. |
(1,0) : élément de courant |
(2,0) : moment magnétique d'un aimant, d'une particule. |
|
Q. Lα. |
L-3 |
L-2 |
L-1 |
L0 |
L1 |
|
rang zéro : scalaire |
|
|
|
(0,0) Charge électrique |
|
|
rang un : vecteur |
|
|
(0,1) : d. linéique |
|
(1,0) dipôle électrostatique |
|
bivecteur. |
|
(0,2) : densité surfacique de charge |
|
|
|
|
trivecteur. |
(0,3) : densité volumique de
charge |
|
|
|
|
|
"ordre 4" |
|
(1,3) : |
|
|
|
:densité volumique de polarisation
|
Q. Lα.T-1 |
L-2 |
L-1 |
L0 |
L1 |
L2 |
|
rang zéro : "scalaire" |
|
|
intensité d'un courant. |
|
|
|
rang un : vecteur |
|
|
|
(1,0) : élément de courant |
|
|
bivecteur. |
(0,2) : densité surfacique de
courant dans un fil. |
|
|
|
(2,0) : moment magnétique d'un aimant, d'une particule. |
|
trivecteur (0,3). |
|
(1,2) : densité surfacique d'élément
de courant. |
|
(2,1) : densité linéique de moment
magnétique. |
|
|
"ordre 4" |
(1,3) : densité volumique d'élément
de courant |
|
(2,2) : densité surfacique de moment
magnétique. |
|
|
|
"ordre 5" |
|
(2,3) : densité volumique de moment
magnétique |
|
|
|
En électromagnétisme, la famille du potentiel et du champ présente
une ambigüité : si on la considère comme famille dépendante de l'action ou de
l'énergie, divisées par la charge électrique, le potentiel électrique prend
une place rassurante de quasi-scalaire (composante temporelle d'un covecteur de
dimension 4), et le champ électrique prend une place de covecteur plus en
accord avec sa définition usuelle comme gradient du potentiel. Mais l'aspect
est plus douteux quant aux positions des gyreurs 
et 
. Certes compatibles, mais peu convaincantes :
|
Mc².Q-1. Lα.T-β |
L-2 |
L-1 |
L0 |
|
|
(0,2) |
(0,1) |
(0,0) |
|
T1 |
champ magnétique |
potentiel vecteur |
flux magnétique |
|
T0 |
|
Champ électrique |
potentiel électrique |
|
M.Q-1. Lα.T-β |
L0 |
L1 |
L2 |
|
|
(1,1) |
(1,0) |
(2,0) |
|
T-1 |
champ magnétique |
potentiel vecteur |
flux magnétique |
|
T-2 |
|
Champ électrique |
potentiel électrique |
Les critères précédents laissent des doutes : faut-il prendre au sérieux ces cinq derniers tableaux ?
La Relativité nous enseigne une connexion en diagonale dans le tableau des grandeurs dynamiques : l'impulsion et l'énergie cinétique sont les quatre composantes d'un vrai vecteur en dimension 4, l'impulsion-énergie, qui est lui, un vrai invariant relativiste.
L'action d'Euler-Hamilton, est aussi un vrai invariant relativiste, et semble scalaire. Mais depuis 70 ans, la mécanique quantique reste ambigüe sur la nature de h et de h, indifféremment quantum d'action (produit intérieur d'une impulsion par une distance), ou quantum de module de moment cinétique (produit extérieur). On ne saura trancher la question que quand la physique théorique aura résolu sa crise actuelle, ce qui peut prendre encore plusieurs dizaines d'années. Nous ne saurions attendre la réponse à ce genre de questions fondamentales, pour remettre de l'ordre dans la physique élémentaire.
5. L'action et le formalisme hamiltonien.
5.1. Noether et le formalisme canonique.
Le théorème de Noether, et le
formalisme de Hamilton, puis les relations d'indétermination de Heisenberg,
nous montrent à l'évidence, que certaines grandeurs sont conjuguées :
|
Coordonnée sans masse. |
Coordonnée massique
(conservative dans les symétries noethériennes). |
Produit des deux coordonnées conjuguées. |
|
déplacement |
impulsion |
action |
|
angle |
moment cinétique |
action |
|
durée |
énergie |
action |
|
(nombre de quanta) ? |
(quantum d'action h) ? |
action |
Or, ces grandeurs canoniquement conjuguées ont toujours même symétrie, et peuvent validement être considérées comme duales, dans un système d'unités centré sur le quantum d'action.
C'est évident si l'on regarde les équations canoniques de Hamilton, où l'énergie du système est exprimée en fonction des coordonnées q et des impulsions généralisées p :
et 
.
Si dans ce système, on regarde le déplacement comme vecteur, l'impulsion est covecteur associé. Dans ce système, le vice-versa est aussi valide : l'impulsion comme vecteur, le déplacement comme covecteur associé.
La durée et l'énergie sont coordonnées duales. En ce sens que les vecteurs de dimension 4 impulsion-énergie, et déplacement-durée, sont duaux.
De même, l'angle et le moment cinétique sont tenseurs duaux. Seuls les angles infinitésimaux, et les angles droits, donnent mathématiquement des gyreurs. Pour garder la structure profonde du tableau, il faut admettre de classer les gyreurs et les rotateurs dans une même famille de tenseurs, dont le nom reste à trouver, et qui sont antisymétriques dans leur restriction au plan stable.
Il faut accepter la coexistence de ces deux systèmes de représentations, celui-ci centré sur l'action et sur le lagrangien, et celui plus connu centré sur la masse, correspondant au formalisme newtonien. Tous deux véhiculent une forte part de réalisme.
Ceci implique que selon le système de représentation, les caractères "vecteur" ou "covecteur" peuvent glisser ou se permuter, et de même les caractères de "gyreur strict", gyreur étendu", "cogyreur étendu". Mais que dans tous les cas, aucun membre de la famille gyreur ne devient membre de la famille vecteur, ni l'inverse. Les symétries vectorielles, et gyratorielles, ont une permanence physique intrinsèque, sur laquelle le physicien peut faire fond, en toute confiance.
La coexistence de ces deux systèmes de représentation, l'un centré sur la masse, l'autre sur l'action, assure des équations physiques, qui soient toutes limitées au premier ordre de dérivation. En effet le nombre deux, l'ordre deux, présent dans les formalismes newtonien et maxwellien classiques, est bel et bien un "nombre magique". Pourquoi justement la dérivation arrêtée à l'ordre 2, et pas 1 ni 3 ni 4 ? La limitation à l'ordre 1 implique le doublement des variables à dériver à l'ordre 1, ce qui était justement déjà réalisé par les formalismes agrangien, et surtout hamiltonien. Le théorème de Noether, et la conjugaison géométrique des conjugués canoniques, que nous venons de mettre en évidence, justifient amplement ce doublement.
Domaine de validité, aussi bien du théorème de Noether, que de la distinction entre grandeurs extensives, et grandeurs intensives : l'espace doit être localement euclidien, autrement dit, localement dépeuplé, avec des champs tous faibles, afin que le postulat de superposabilité soit approximativement exact. Autrement dit, les déplacements mis en jeu sont petits devant la distance aux autres objets massifs notables.
5.2. En translation, avec la somme des forces.
Nous pouvons étudier le résultat de la somme des forces de deux façons : le long du chemin parcouru par le centre d'inertie du système, ou le long de la durée qu'a pris le mouvement.
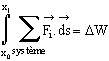
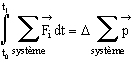
Autrement dit, sous forme différentielle :
(avec 
)
Par définition, la quantité ΔW, est appelée le travail de cette force, durant le déplacement de son point d'application. Cette quantité, travail, a la dimension physique d'une énergie.
est l'expression physiquement correcte, car des
deux côtés du signe égale, figurent des grandeurs extensives, ainsi
qu'il est de règle pour toute loi de conservation. Alors que ce n'est pas
réalisé dans la formule analytisée ultérieurement par Newton : 
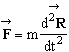. Là seule la masse m est grandeur extensive; on ne
voit donc pas apparaître un grand principe, mais une magie étrange, portant
apparemment sur la cinématique.
Une grandeur est extensive, si elle s'additionne avec l'ajout de sous-systèmes. Deux masses de 1 kg font une masse de 2 kg. La masse est grandeur extensive. Si vous poussez à deux votre voirture en panne, l'équipe est deux fois plus forte qu'un seul homme : la force est grandeur extensive. Si vous liez côte à côte deux mobiles dont la quantité de mouvement est de 1 kg.m/s chacun, l'ensemble a une quantité de mouvement de 2 kg.m/s. La quantité de mouvement est grandeur extensive.
La vitesse et l'accélération ne sont pas des grandeurs extensives. Si vous mettez côte à côte deux mobiles dont la vitesse est de 1 m/s chacun, l'ensemble n'a pas une vitesse de 2 m/s.
Ecrivons ces lois de conservation :
Conservation de l'impulsion
: 
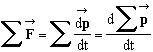
Conservation du moment cinétique
: 
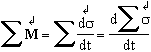
Conservation de la masse :
Conservation de la charge électrique :
6. Conclusion provisoire en proverbes.
La mécanique réclame le double jeu d'unités de base : M,L,T,Q, et A, L, T, Q (Le Kelvin, la candela, la mole ne jouent pas de rôle en mécanique). Le premier est basé sur la masse, le second sur l'action, dont le quantum est h (ou h, si on prend le radian pour unité). Le premier semble incontournable, au moins en physique macroscopique, le second est inévitable, surtout en physique quantique. L'ambigüité entre les deux systèmes semble intrinsèque à la nature, et non aux physiciens.
Le passage d'un système d'unités à l'autre ne bouleverse jamais le type fondamental de symétrie d'une grandeur : le genre gyreur, et respectivement le genre vecteur sont stables dans ce passage.
La mécanique hamiltonienne, puis la mécanique statistique faisaient déjà grand usage de ce double système de coordonnées, dans l'espace d'extension en phases à six dimensions abscisse-impulsion. L'avantage étant de pouvoir écrire les grandes lois de conservation entièrement en dérivations premières, sans dérivées secondes, et entièrement en grandeurs extensives.
L'analyse dimensionnelle permet de prédire la valence tensorielle nette d'une grandeur physique, mais ne permet de rien prédire de ses symétries, et donc rien non plus de ses valences covariantes ni contravariantes. Il est indispensable de tenir compte du caractère tensoriel des densités et capacités volumiques, et des densités et capacités surfaciques.
Deux grandeurs conjuguées dans le théorème de Noether, sont
en même temps conjuguées canoniques, et ont même symétrie tensorielle. Du moins
en physique élémentaire, macroscopique.