L'article précédent, contient tous les lemmes repris de la pratique cristallographique, les définitions, les notations, ainsi que toutes les représentations des gyreurs unitaires, rotateurs et projecteurs, dans les espaces de dimension 2 , 3 et 4.

1. Module d'un gyreur.

La physique exige la loi de multiplication par un scalaire : Module de λJ = λ(module de J), pour tout λ dans R.

Un gyreur étendu est homogène à une surface, donc son module est une expression bilinéaire aux deux vecteurs dont il est produit extérieur. A deux dimensions (rang du gyreur = dimension de l'espace), le module d'un gyreur, s'identifie à la racine carrée du déterminant.

En dimension 3, le déterminant d'un tourneur (une forme de degré 3 sur les coefficients) est toujours nul.

C'est le second invariant euclidien, somme des mineurs diagonaux, qui donne la solution. Ces déterminants d'ordre 2, correspondent aux trois projections du gyreur sur les trois plans de base, ici orthogonaux.

1.1. Cas d'un repère orthonormal, donc coordonnées de gyreur antisymétriques :

Carré du module de 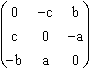= + + = a² + b² + c²,

car le tenseur métrique est alors la matrice unité. Les composantes strictes d'un gyreur unitaire satisfont à l'égalité :

(sin α)² + (cos α.cos β)² + (cos α.sin β)² = (sin α)² + (cos α)² = 1 .

1.2. Cas général.

Expression du carré du module d'un gyreur B quelconque, sur une base dont g est tenseur métrique :

= .

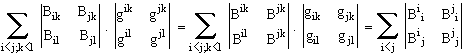C'est valable aussi pour tout autre tenseur de rang 2 et de déterminant nul, tel que le tenseur d'inertie.

2. Direction de plan stable d'un gyreur sur R³.

2.1. Reconnaître qu'un gyreur et un vecteur sont coplanaires.

2.1.1. Si le gyreur est déjà connu comme produit extérieur de vecteurs.

On est ramené à la question élémentaire, de trois vecteurs coplanaires. Il suffit de former leur déterminant, et constater qu'il est nul. Soient [q,r,s], [u,v,t] et [d,e,f] les coordonnées de ces vecteurs.

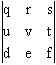= 0.

2.1.2. Si le gyreur est connu par ses coordonnées complètes.

Multiplier le vecteur par le gyreur. Le produit extérieur du produit, par le vecteur original, doit être nul.

V^(T.V) = 0.

2.2. Déterminer le sous-espace plan stable d'un gyreur.

La rotation d'un quart de tour, laisse le sous-espace plan stable globalement invariant, donc le tourneur appliqué au covecteur d'un plan représentant l'équiplan, donne un résultat nul (une variation nulle) :

Cas facile : le gyreur est déjà exprimé en coordonnées antisymétriques :

L'équation (a; b; c) . 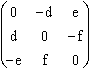= 0 n'a qu'une solution, à une constante multiplicative α arbitraire près : f = α.a, e = α.b, d = .c. On peut conclure que le gyreur général, de coordonnées 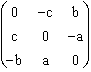est dans l'équiplan de coordonnées covariantes (a; b; c), d'équation ax + by + cz = 0.

Ce cas simple se produit chaque fois que le gyreur est exprimé en coordonnées homogènes, deux fois covariantes, ou deux fois contravariantes. Cela n'arrivera en coordonnées mixtes (état primitif du gyreur strict) que si le repère est orthonormal. Dans un autre repère, il faudra soit le convertir en coordonnées homogènes, par le jeu du tenseur métrique, soit résoudre le système général :

(a; b; c) . 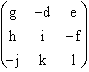= 0 .

2.3. Déduire d'un gyreur étendu, deux vecteurs dont il est produit extérieur.

2.3.1. Lemme : arêtes communes à un plan, et aux plans de base.

Tout plan comporte au moins une direction de droite parallèle à un des plans de base. Cherchons laquelle.

Etant donnés un plan de coordonnées covariantes (H,K,L). Nous cherchons son arête [u, v, t]avec un plan de base, (1,0,0) pour fixer les idées. Par application du lemme précédent :

u = 0

v = VL (V, volume de la maille de base)

t = -VK. Soit finalement la droite V[0, L, -K], au signe éventuel près.

Par permutation circulaire, nous obtenons les deux autres arêtes : V[-L, 0, H] et V[K, -H, 0]. Chacun de ces jeux de coordonnées est pourvu de sens tant qu'au moins une coordonnée de droite n'est pas nulle.

2.3.2. Calcul en base orthonormale.

En coordonnées orthonormales, le gyreur B de coord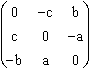onnées , a dans son plan stable le plan de coordonnées (a; b; c). Ce plan a pour arêtes communes avec les plans de base, les droites de coordonnées

V[0, c, -b], V[-c, 0, a] et V[b, -a, 0]. Au moins une de ces droites est définie, par des coordonnées non toutes nulle. Choisissons-la : V[b, -a, 0] pour fixer les idées, si ab Différent de 0.

Nous voulons le second vecteur dans le plan perpendiculaire, de coordonnées covariantes (b; -a; 0).

Il nous reste à déterminer l'arête intersection de ce plan avec le plan de B. Elle a pour coordonnées :

(a; b; c) ^ (b; -a; 0) = [ca; cb; -(a² + b²)].

Par ailleurs, nous connaissons le module de B : = = 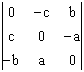a² + b² + c².

Or nous connaîssons le module du vecteur [b, -a, 0] : ,

et celui de [ca; cb; -(a² + b²)] : .

Nous pouvons donc imposer à nos vecteurs d'être non seulement perpendiculaires, mais de même module.

V₁ = [b, -a, 0], V₂ = .

On vérifie : T = V₁ ^ V₂.

2.4. Projection intérieure d'un vecteur sur une direction de plan.

Projeter le vecteur [u,v,t] sur le plan (H,K,L). Nous avons à formuler la matrice de projecteur, qui maintienne un vecteur parallèle au plan (H,K,L), et dont le noyau soit la droite perpendiculaire (en base orthonormée, les indices de la droite seraient [H, K, L]). Nous voulons un opérateur de valence totale nulle, qui laisse [u,v,t] invariant quand [u,v,t] . (H,K,L) = 0.

Nous avons vu que le carré d'un gyreur strict unitaire, est l'opposé du projecteur sur son plan stable.

Notre problème est résolu dès qu'on sait déduire un gyreur unitaire du covecteur (H,K,L).

La première opération est de normaliser le covecteur représentant le plan, soit résoudre l'équation :

(H,K,L) . (H,K,L) = g^iju_i u_j = 1.

Dans le cas particulier de coordonnées orthonormales :

Pint(H,K,L) = . =

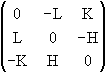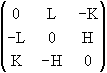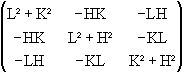
Son module est le carré du module du gyreur de départ, donc 1 après normalisation de (H,K,L).

C'est donc bien la matrice de projection cherchée, appliquable à un vecteur comme à un gyreur.

Au gyreur unitaire 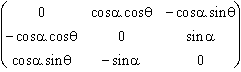correspond le projecteur

Pint(α, θ) = 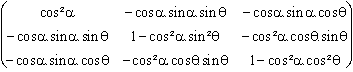. Forme générale orthonormée.

C'est aussi le projecteur extérieur à la droite de vecteur directeur unitaire : [sin α; cos α.sin
θ; cos α.cos θ].

Projecteur et gyreur ont même noyau, la droite de vecteur directeur unitaire : [sin α; cos α.sin θ; cos α.cos θ].

Dans le cas général : Pint(H,K,L) = . .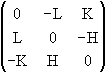

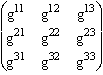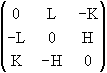
On l'a déjà vu, le plan (H,K,L) contient les droites représentées par les vecteurs [h; -k; 0], [0; k; -l] et [-h; 0; l]. On peut vérifier que ces vecteurs sont invariants par Pint(H,K,L).

En toute base, tout projecteur intérieur sur un (équi)plan a pour polynôme caractéristique : λ(1-λ)².

2.5. Projection extérieure d'un vecteur à une direction de plan.

La somme des projections intérieures et extérieures, est la transformation identique. On obtient donc la projection extérieure par différence : Pext(H,K,L) = - Pint(H,K,L) =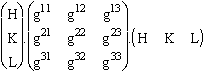

En coordonnées orthonormales,

Pext(H,K,L) = = .

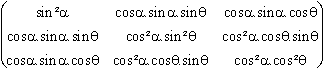C'est aussi le projecteur intérieur sur la droite de vecteur directeur unitaire : [sin α; cos α.sin θ; cos α.cos θ].

En toute base, tout projecteur extérieur à un (équi)plan a pour polynôme caractéristique : λ²(1-λ).

2.6. Applications des projections intérieures et extérieures :

2.6.1. Trajectoire d'une particule chargée, dans un champ magnétique d'orientation quelconque : on doit bien décomposer la vitesse, en projection intérieure sur , qui est déviée par , et projection extérieure invariante.

Nous n'avons même pas besoin d'extraire un gyreur unitaire, il suffit de calculer le cogyreur inverse. Il nous suffit de multiplier le gyreur champ magnétique, par le cogyreur dual (qui a bien le même plan stable, l'angle opposé, le module inverse, et l'unité physique inverse), pour obtenir le projecteur intérieur cherché.

Expression du cogyreur dual de B : -B /||B||².

Expression du projecteur intérieur sur le plan stable de B : -B.B /||B||².

2.6.2. Produit doublement contracté, "biscalaire" de deux gyreurs A et B :

Formons d'abord leur produit contracté (autrement dit : matriciel ordinaire) : ^tA.B en coordonnées orthonormales, -A.g.B en coordonnées quelconques, puis prenons en l'invariant d'ordre 2. Nous avons vu plus haut la cohérence avec le calcul du module.

On peut aussi passer par la matrice de projection intérieure, qui peut donner un calcul plus simple.

Calculons le produit contracté simple de deux gyreurs, de la même façon que nous avions obtenu le projecteur associé à un gyreur, dans le cas simplifié d'une base orthonormale :

. =

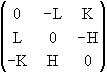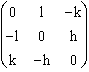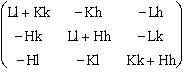
Cette matrice n'est pas symétrique. Son déterminant est nul, son second invariant vaut (Hh + Kk + Ll)²; et sa trace vaut 2(Hh + Kk + Ll).

Nous reconnaîssons le résultat classique : le produit biscalaire de deux gyreurs, est égal au produit scalaire des covecteurs associés à leurs équiplans respectifs, et ayant mêmes modules : Hh + Kk + Ll.

En bases quelconques, il faut faire intervenir le tenseur métrique exactement de la même façon que pour le module d'un gyreur. Le tenseur métrique n'intervient pas, si l'on a eu la bonne idée d'exprimer un gyreur en coordonnées covariantes, et l'autre en coordonnées contravariantes.

Applications : calcul de la densité d'énergie d'un champ magnétique, par exemple pour l'interprétation de la manipulation classique: les spectres de limailles de Faraday.

Nous pouvons de même calculer le cosinus de l'angle de deux gyreurs nus stricts. Il faut prendre le dual de l'un des gyreurs : cos(A,B) = -A.B/||B||² = -A.B/||A||² = -A.B/(||A||.||B||).

3. Changements de coordonnées quelconques.

3.1. Une base non orthogonale en dimension 2. Exercice heuristique.

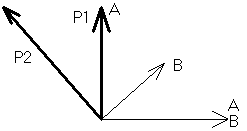
3.1.1. Soit A l'ancienne base, B la nouvelle base.

Soit la matrice de changement de base. On vérifie qu'elle est bien régulière, c'est à dire de déterminant non nul : = 0,5.

Modules des vecteurs de base : 1, et 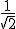$\frac 1 {\sqrt 2}$ . Angle : Arcos( 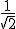$\frac 1 {\sqrt 2}$ ) = π/4.

On forme son tenseur fondamental, ou tenseur métrique, dont les coordonnées sont les produits scalaires (intérieurs contractés) des vecteurs de la nouvelle base :

g = = . Evidemment, il est symétrique. Son déterminant est le carré du déterminant de la matrice de changement de base : = = 0,25.

Le tenseur métrique réciproque, 2-contravariant se définit comme inverse de g : .

Matrice inverse : . Le déterminant de T^-1 est évidemment 2, inverse de celui de T.

Comment ne pas s'embrouiller dans l'ordre des transpositions ? g = , alors que .

Pour g, la règle est qu'un vecteur ligne (transposé d'un nouveau vecteur de base) multiplie un vecteur colonne (nouveau vecteur de base).

Pour , il faut se souvenir que .g = 1, donc . = = 1 = = ..

Il sera intéressant de considérer les valeurs propres et vecteurs propres de T. Polynôme caractéristique :

= (λ-1)(λ- 0,5). Donc les valeurs propres sont 1 et ½.

. = , ou . = = 0.

Si λ = 1, x quelconque, y nul. P₁ = .

Si λ = 0,5, y quelconque, x = -y. P₂ = .

Les vecteurs propres ne sont pas orthogonaux

(la matrice n'est ni hermitienne, ni antihermitienne).

3.1.2. Nouvelles coordonnées du gyreur selon l’exemple.

Posons les nouvelles coordonnées de nos vecteurs et , pour l'exemple de la rotation à vitesse uniforme (Nous omettons volontairement les coefficients physiques, et les unités, ne nous concentrant que sur la géométrie. Les vecteurs de base seront sous-entendus.) :

Pour vérifier l'orthogonalité de avec , il faut utiliser le tenseur métrique, pour former le produit scalaire :

. =

Posons la matrice comme quotient de la matrice carrée (,) par la matrice carrée (,)

= Horreur ! elle n'est plus antisymétrique !

Pourtant, on vérifie bien que :

. = = (,) = (,).

Vérifions les nouvelles coordonnées de par la formule générale :

. . = .

La matrice duale (unitaire) reste bien égale à l'opposé : ()^-1 = = - .

3.1.3. Les coordonnées mixtes ne restent pas antisymétriques dans les bases non othonormées.

Toutefois, les invariants de tenseurs de rang 2, en coordonnées mixtes, se maintiennent dans les changements de base, car ils sont liés aux valeurs propres, et au polynôme caractéristique : = (λ+1)(λ-1) + 2 = λ² + 1. Il est inchangé.

Donc aussi le déterminant : -1 + 2 = 1. Vérifions pour la trace de , elle vaut toujours -1 + 1 = 0.

Tout s'est bien maintenu. On est conduit à penser que c'est là une caractéristique des coordonnées mixtes, une fois covariantes, et une fois contravariantes, leur valence totale étant nulle, elles conservent les invariants euclidiens, alors qu'elles ne peuvent conserver l'antisymétrie. Nous aurons à le vérifier en dimension trois.

3.2. L'antisymétrie des coordonnées homogènes se maintient dans toutes les bases.

Complètement covariantes,

Formons , qui est entièrement covariante, et antisymétrique.

Complètement contravariantes.

, entièrement contravariante, et antisymétrique.

Dans les trois cas (coordonnées mixtes, covariantes et contravariantes), nous avons sciemment omis les unités physiques, et même les coefficients physiques, nous concentrant sur la représentation tensorielle de la géométrie.

Que deviennent leurs invariants ?

Coordonnées complètement covariantes :

Tr = 0 = 0,25 = , donc l'invariant réel semble être . = 1 .

Coordonnées complètement contravariantes :

Tr = 0 = 4 = , donc l'invariant réel semble être . = 1 .

Cela se comprend aisément : le module d'un produit extérieur, est le produit des modules des (co)vecteurs orthogonaux, termes de la multiplication. L'extension en dimension 3, exigera tous les mineurs du tenseur métrique.

3.3. Une base non orthogonale en dimension 3. Exercice heuristique.

3.3.1. Soit A l'ancienne base, B la nouvelle base.

Soit 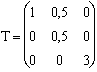la matrice de changement de base.

On vérifie qu'elle est bien régulière, c'est à dire de déterminant non nul : 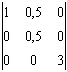= 1,5.

Modules des vecteurs de base : 1, 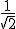1/sqrt 2 , et 3. Angles : π/4, π/2 et π/2.

Ses mineurs diagonaux : = 0,5, = 3, = 3/2.

Un mineur non diagonal non nul : = 3/2. La trace ne joue aucun rôle.

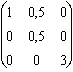
On forme son tenseur métrique : g = = . =

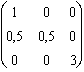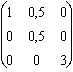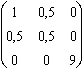
Son déterminant est le carré du déterminant de la matrice de changement de base : = = 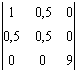2,25.

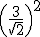Mineurs diagonaux de g : = 0,25 = 0,5², = 9 = 3², = 9/2 = Carré de 3 sur rac2 .

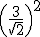Deux mineurs non diagonaux non nuls : = 9/2 = Carré de 3 sur rac2 chacun.

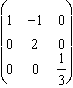
Matrice inverse : 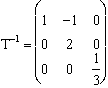. Son déterminant : 2/3. La trace ne joue aucun rôle.

Mineurs de T^-1 : = 2, = 1/3, = 2/3, = -1/3.

Le tenseur métrique, 2-contravariant : = = .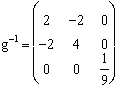

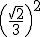Mineurs diagonaux de : = 4 = 2², = 2/9 = carre de Rac 2, sur 3 , = 4/9 = (2/3)².

Deux mineurs non diagonaux non nuls : = -2/9 chacun.

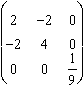
Calculons les transformées des trois gyreurs unitaires, dans cette nouvelle base.

Sur yOz : J_yz = 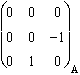, sur zOx : J_zx = 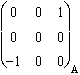, et sur xOy : J_xy = .

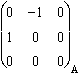Calculons les coordonnées mixtes :

Pour J_xy : 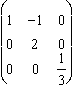. . 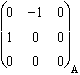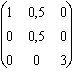= 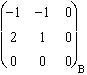, de module euclidien 1.

Son plan stable : (a; b; c) . 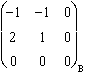= = 0, donc b = a = 0.

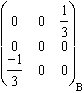
Soit le plan de coordonnées (0; 0; 1)_B (normalisé à (0; 0; 3)_B).

Les projecteurs sur le plan stable : Pint(J_xy) = 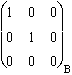. Pext(J_xy) = .

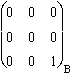Pour J_yz : . . 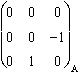= 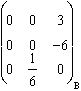, de module euclidien 1.

Son plan stable : (a; b; c) . 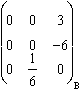= = 0, donc c = 0, et a = 2b.

Soit l'équiplan de coordonnées (2; 1; 0)_B (normalisé à (1; 0,5; 0)_B).

Les projecteurs sur le plan stable : Pint(J_yz) = 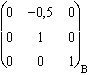. Pext(J_yz) = .

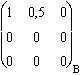Pour J_zx : 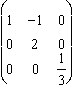. . 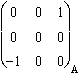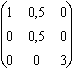= 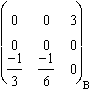, de module euclidien 1.

Son plan stable : (a; b; c) . 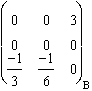= = 0, donc c = a = 0.

Soit l'équiplan de coordonnées (0; 1; 0)_B (normalisé à (0; 0,5; 0)_B).

Les projecteurs sur le plan stable : Pint(J_zx) = 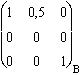. Pext(J_zx) = .

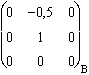Remarque : une fois normalisés, les covecteurs représentant ces équiplans stables, recomposent la matrice de changement de base.

Nous avons donc bien conservé la forme de calcul du module d'un gyreur strict, exprimé dans ses coordonnées mixtes, en base quelconque, comme somme des trois mineurs diagonaux. Les traces sont restées nulles.

Retenons qu'en coordonnées mixtes, sur n'importe quelle base, on calcule bien le module d'un gyreur strict par la racine carré de la somme des mineurs diagonaux d'ordre 2.

Et en coordonnées homogènes ? L'antisymétrie des coordonnées est rétablie, mais le calcul du module se complique.

Menons le calcul sur un exemple de type (2,0), le produit extérieur de deux vecteurs de la nouvelle base :

X = ^ =

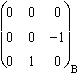
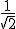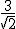Modules des deux vecteurs concernés : $\frac 1 {\sqrt 2}$ , et 3. Angle : π/2. D'où ||X|| = 3 sur rac 2 .

Y = ^ =

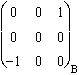
Modules des deux vecteurs concernés : 1, et 3. Angle : π/2. D'où ||Y|| = 3.

Z = ^ = .

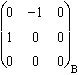Modules des deux vecteurs concernés : 1, et 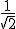$\frac 1 {\sqrt 2}$ . Angle : π/4. D'où ||Z|| = 0,5.

Résultat intéressant : ce sont justement les racines carrées des trois mineurs diagonaux du tenseur métrique g.

Vérifions notre conjecture sur les transformés contravariants de J_yz, J_zx,J_xy :

Pour J_xy :

J_xy en coordonnées mixtes : 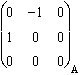et .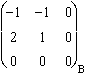

J_xy (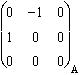) . g^-1 = . = . =

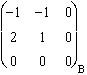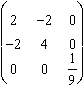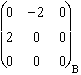. = = 2 Z. Unique mineur : = 4.

On le multiplie par le mineur correspondant de g : . = 1

Pour J_zx :

J_zx (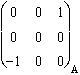 ) . g^-1 = . = 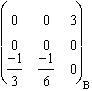. = = Y/3.

Unique mineur : = 1/9, d'où : . = 1. Bonne valeur.

Pour J_yz :

J_yz (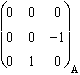 ) . g^-1 = . = 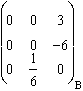. = = Y/3 + 2X/3.

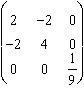
. + . + . + . = 1

La somme des produits de tous les mineurs de degré 2 donne bien le bon carré du module.

Nous avons donc vérifié que la seule loi du carré du module d'un gyreur B quelconque, qui ne soit contradictoire, est :

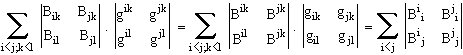
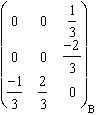
En coordonnées entièrement covariantes, l'antisymétrie est aussi retrouvée :

g . J_zx () = = . = .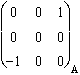

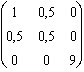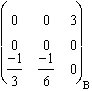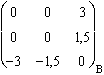Calculons son carré du module, par les mineurs de degré 2 de :

. + . + . + . = 2 +1 -1 -1 = 1.

C'était le seul cas difficile. Les deux autres sont évidents.

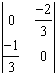
g . J_yz (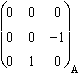) = = 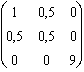. 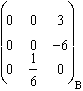= 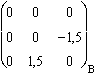, de module 1.

g . J_xy (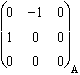) = = 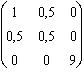. 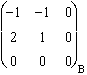= 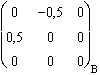, de module 1.

On calcule donc bien le module, avec tous les mineurs du tenseur métrique réciproque.

Dans tous les cas, le tenseur métrique tient toutes ses promesses pour les calculs des invariants. Alors que l'invariance de la métrique était totalement impossible dans les fictions en "produit vectoriel", toujours en porte-à-faux. Or ce sont bien les invariants qui sont vitaux pour la physique.

Tous ces calculs sont faciles à automatiser sur un calculateur de poche matriciel, comme les fabricants majeurs en proposent.

4. Conclusion.

Ici, nous avons développé le calcul sur les êtres plans, tels que les gyreurs, et sur leurs relations avec les êtres vectoriels. Nous espérons avoir démystifié les calculs géométriques nécessaires à la physique élémentaire.

La métrique en coordonnées quelconques, réclame en tous cas le tenseur métrique, donc réclame de cesser de maltraiter son outil mathématique. Jusqu'à présent, le tenseur métrique et la discipline tensorielle avaient été réservés à des enseignements de haut niveau. Puis diplomatiquement, on les biffait aussitôt, en retraduisant dans les fictions vectorielles usuelles [1]. Et chaque physicien de base, cristallographes exceptés, de conclure aussitôt, qu'on l'encombrait d'inutilités de trop haut niveau. On n'avait pas encore entrepris d'expliquer les choses mathématiques élémentaires de la physique, à niveau élémentaire. C'est pourquoi, dans un article précédent, nous avons multiplié les moyens graphiques élémentaires.

Nous avions tous eu la malchance que l'enseignement que nous avions subi, maltraitait les plans, et les êtres géométriques plans, en les remplaçant par des fictions vectorielles. La plupart des manuels courants en mathématiques [2], changeaient subrepticement de définition des vecteurs, toutes les trois pages... Ce laxisme confus a duré bien trop longtemps.

La diplomatie, et les intimidations entre citadelles académiques, ayant leurs raisons que la raison ne connaît pas, il ne fallait compter ni sur les mathématiciens - excepté Poincaré ? excepté E. Cartan ? excepté H. Weyl surtout - pour vérifier le bien fondé physique de ce qu'ils enseignaient "à usage des physiciens", ni sur les physiciens - excepté Einstein ? - pour expliquer à plat, en clair, aux mathématiciens le cahier des charges des outils nécessaires. Le résultat standard ressemble fâcheusement à une mystification mutuelle involontaire.

Un jour prochain, avec les mêmes outils cindyniques[3] qu'on applique à l'analyse des accidents, comme Bhopal, ou le Titanic, il faudra bien examiner les causes structurales de ladite mystification. Le sentiment d'infaillibilité, la carence éthique (la discipline sémantique, par exemple, est-elle, ou non, un de nos devoirs envers nos lecteurs ?), les frustrations mutuelles, les marquages abusifs de frontières par le mépris envers autrui, les carences spécifiques en épreuve de réalité (les uns manquant d'épreuve de réalité concrète, les autres méprisant l'épreuve de réalité abstraite), ont déjà été attestées, et parfois manifestées avec véhémence. Les causes purement contingentes, pourtant nombreuses, ont le dos un peu trop large...

[1] Exemple : Léon Brillouin; Les tenseurs en mécanique et en Electricité. Masson. Paris 1938.

[2] Par exemple, P. Vissio & R. Cluzel; Calcul vectoriel, initiation au calcul matriciel. Delagrave 1965.

[3] Cindynique : science du risque et du danger.

Pratique de l’algèbre des gyreurs.

Auteur : Jacques Lavau

0.1. Prérequis :