Lemmes pour l'algèbre des gyreurs.

1 Définitions, notations.

2 Rappels de métrique.

2.1 Généralités sur l'équation d'un plan.

2.2 Tenseur métrique d'un réseau (d'une base euclidienne en général)

2.3 Expression du produit scalaire.

2.4 Longueur, ou module, d'un vecteur.

2.5 Tenseur métrique réciproque.

2.6 Application : module ("co-longueur") de covecteurs.

2.7 Angle de droites.

2.8 Angle de plans.

2.9 Parallélisme et inclusion de droites dans un plan

2.10 Angle de droite et plan.

2.11 Direction d'arête intersection de deux plans.

2.12 Définition d'une direction de plan par deux vecteurs non colinéaires.

2.13 Vraies et fausses équivalences.

3 Gyreurs unitaires. Approche sur bases orthonormales.

3.1 Génération en dimension 2.

3.2 Génération en dimension 3.

4 Conclusion provisoire.

1     Définitions, notations.

Rang d'une matrice.

Le rang d'une matrice (ou d'un tableau) est l'ordre maximum de déterminant non nul extrait de cette matrice.

Valences de variance.

Définition :      Sur un espace vectoriel E, de dimension n, on définit une matrice n × n de changement de base, comme celle qui exprime la nouvelle base B' dans l'ancienne base B : B' = T.B.

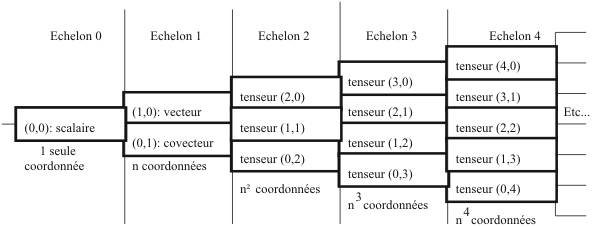
Définition :      Dans un espace vectoriel, un tenseur est un être géométrique présentant un caractère de réalité, donc doué d'une permanence, malgré toutes les différentes façons de le regarder et de l'exprimer.

Définition :      Une suite de coordonnées est tensorielle, autrement dit est le descripteur d'un tenseur p fois covariant, m fois contravariant, si et seulement si, lors d'un changement de coordonnées, elle se transforme par p multiplications (à droite) par la matrice de changement de base, et m multiplications (à gauche) par la matrice inverse. Ceci lui donne compétence pour décrire les grandeurs tensorielles, êtres géométriques classables selon leur dépendance à l'orientation dans l'espace vectoriel.

On nomme alors l'entier p, la valence covariante, m la valence contravariante, et m-p la valence totale. Béklémichev utilise la notation concise : tenseurs de type (m,p). Les vecteurs sont donc de type (1,0), et les covecteurs de type (0,1). Nous compterons donc les gyreurs stricts comme du type (1,1), et les gyreurs étendus comme du type (2,0), les cogyreurs étendus en type (0,2). R. Penrose et W. Rindler proposent une notation encore plus logique pour la valence : .

Notations renforçant le contrôle de type :

Comme il est peu pratique de multiplier les généralisations de la flèche, qui surmonte les lettres désignant des vecteurs, mieux vaut envisager une notation qui intègre le type de variance :

Pour un gyreur strict :              .           Pour un gyreur étendu : . Pour une capacité, comme un volume : .

Pour une masse volumique : , etc.                       ou , , .

Ce garde-fou complète le monôme dimensionnel (déjà maîtrisé au 17e siècle par l'abbé Marin Mersenne).

Livret de famille des tenseurs sur un espace vectoriel :

Symétrie, antisymétrie.

Symétrie d'une expression matricielle ou tensorielle : Aucune coordonnée ne change de valeur quand on permute deux indices : B_ij = B_ji. S'il y a plus de deux indices, on distinguera entre une symétrie sur certaines paires définies d'indices, et une symétrie totale, pour toutes les permutations possibles.

Antisymétrie d'une expression matricielle ou tensorielle : chaque coordonnée change de signe, en gardant sa valeur absolue, quand on permute deux indices B_ij = - B_ji. S'il y a plus de deux indices, on distinguera entre une antisymétrie sur certaines paires définies d'indices, et une antisymétrie totale, pour toutes les permutations possibles.

Livret de famille des multivecteurs sur un espace vectoriel :

Les multivecteurs sont les tenseurs complètement antisymétriques.

Les multivecteurs non nuls en dimension 2 :

Les multivecteurs non nuls en dimension 3 :

Les multivecteurs non nuls en dimension 4 :

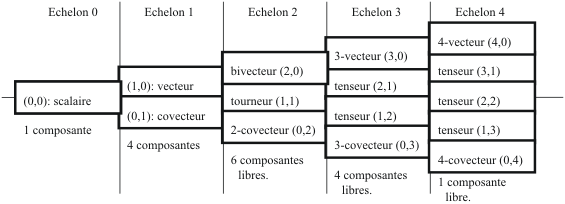
Dans le nombre de composantes strictes libres, on reconnaît le triangle de Pascal (coefficients du binôme) :

1; 2; 1.

1; 3; 3; 1.

1; 4; 6; 4; 1. Etc.

Le rang d'un p-vecteur non nul, sur un espace de dimension n, avec p n, est toujours p.

Piège de langage : on a souvent dénommé "quadrivecteur" un vecteur tout à fait ordinaire, mais dans l'espace quadridimensionel de Minkowski (car dans l'esprit du physicien de base, "vecteur", ça voulait dire trois : trois composantes). Par 4-vecteur, nous désignons un produit extérieur de 4 vecteurs.

2 Rappels de métrique.

Pour ne pas réinventer la roue, nous emprunterons au savoir-faire des cristallographes, qui utilisent fructueusement le calcul tensoriel. Chez eux, "indice", signifie coordonnée.

On s'intéressera rarement à un plan précis (passant par exemple par un point donné), et souvent à la direction de plan, autrement dit, à la classe d'équivalence des plans parallèles.

Il serait souhaitable de distinguer par le vocabulaire, sans longue périphrase, mais la tradition a oublié de le faire. On pourrait suggérer équiplan; de même équidroite pour la classe d'équivalence des droites parallèles. Il se poserait un problème pour la classe d'équivalence des droites orientées, axes, car équiaxe fait collision avec un terme de symétrie en physique et en mécanique des solides. Sous cette convention, on remarque qu'en cristallographie, "plan" signifie le plus souvent équiplan, et "droite" signifie le plus souvent équidroite.

2.1      Généralités sur l'équation d'un plan.

En cristallographie, on introduit les indices de plan, à partir des positions des noeuds, intersection du plan cristallographique, avec les trois axes de coordonnées. Le plan coupe les axes en des points d'indices (entiers, ou infinis) [h,0,0], [0,k,0] et [0,0,l]. On utilise les crochets [ ] pour les indices de droites, ou de vecteurs.

Les entiers h, k, l, appartiennent à (infini inclus, zéro exclu). Soit M le plus petit commun multiple de ceux de ces entiers qui sont finis. On forme alors les indices de plan H, K, L Î Z :

H = M/h                        (donc hH = M)

K = M/k                        (donc kK = M)

L = M/l                          (donc lL = M)

Par construction, ils sont premiers entre eux. On écrit ces indices de Miller de plan :                (H, K, L).

Les séparateurs entre indices, virgules ou points, sont souvent omis, et remplacés par un simple blanc, car les indices cristallographiques supérieurs à 9 sont rarement considérés.

Ceci est bien cohérent avec l'équation du plan :     

que l'on peut aussi écrire avec les indices covariants, de Miller :               Hx + Ky + Lz = M.

Tout plan se caractérise dans un repère, par son équation : Hx + Ky + Lz = M. En cristallographie, les coordonnées covariantes de la direction de plan H, K, L, sont des entiers relatifs (généralement premiers entre eux), et sont nommées les indices de Miller du plan.

Dans le cas général, on considère le covecteur (type (0,1)) de coordonnées covariantes (p; q; r), qui représente le plan, par l'équation : px + qy + rz = M. On peut choisir M = 1 dans de nombreux cas, notamment si l'on veut définir un covecteur comme "inverse" d'un vecteur. Sous cette définition, le covecteur est un bon modèle mathématique d'un plan.

Mais si l'on ne s'intéresse qu'à la direction de plan, M n'a aucune importance, et on peut le prendre nul. Le covecteur n'est alors défini qu'à une constante multiplicative près, et au signe près. Le covecteur contient plus d'informations que nécessaire pour décrire l'équiplan.

On n'accède aux relations métriques avec les vecteurs hors de ce plan que par le tenseur métrique. Ce n'est que dans le cas particulier d'un repère orthonormal, qu'un vecteur de coordonnées (contravariantes) [p, q, r], est perpendiculaire au plan de coordonnées covariantes (p, q, r).

2.2     Tenseur métrique d'un réseau (d'une base euclidienne en général)

Par définition, ses composantes se définissent à partir des vecteurs de base B, et de leurs angles. Nous les exprimons par leurs coordonnées dans l'espace E × E, où chaque E est rapporté à ladite base B :

g _ij = |e_i| |e_j| cos(e_i, e_j). g, car il a d'abord été connu comme "matrice de Gram".

Il est deux fois covariant, c'est à dire varie comme le carré de vecteurs du même genre que les vecteurs de base.

Dimension : si les vecteurs de la base sont homogènes et en mètres, le tenseur métrique est en mètres carrés.

En détail, si l'on a défini a, b, et c comme les modules des vecteurs de la base , , ,

et les angles : = ( , ), = ( , ), = ( , ), alors                                        g_B,B = .

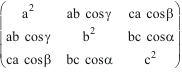D'où les relations inverses :        a = , et similaires,

       = , et similaires par permutations circulaires.

Volume de la maille élémentaire :

 = abc , avec =

2.3     Expression du produit scalaire.

Soient les vecteurs [u,v,t] et [d,e,f], que nous réécrivons sous forme tensorielle uⁱ et v^j.

[u,v,t] . [d,e,f] = g _ij uⁱ v^j

2.4     Longueur, ou module, d'un vecteur.

Soit ce vecteur [u,v,t], que nous réécrivons sous forme tensorielle uⁱ.

[u,v,t] . [u,v,t] = g _ij uⁱ u^j

Il faut en prendre la racine carrée, pour obtenir la longueur, généralisée en module.

Application : longueur du vecteur [111] en réseau cubique, de paramètre a : a.

En effet, le tenseur métrique d'un réseau cubique, se réduit à a² fois le tenseur unité.

2.5     Tenseur métrique réciproque.

On peut définir le tenseur métrique deux fois contravariant, comme inverse du précédent :            g_ij . g^ij = 1

Dimension : si les vecteurs de la base sont homogènes et en mètres, le tenseur métrique est en m^-2.

(On peut éventuellement définir la métrique du réseau réciproque un peu différemment, à une constante multiplicative près, pour la faire coïncider avec celle des vecteurs d'onde dans ce même cristal).

Les cristallographes préfèrent considérer ce tenseur 2-contravariant, comme le tenseur fondamental d'un réseau réciproque (synonyme de dual, au sens des algébristes, depuis Cayley). Les vecteurs de base du réseau réciproque sont normaux aux plans {100}. Dans le réseau réciproque, les vecteurs correspondent aux normales aux plans du réseau réel. Les longueurs de ces vecteurs, sont les inverses des distances réticulaires entre les plans et l'origine. D'où l'expression du produit scalaire de deux covecteurs représentant des plans d'indices (H,K,L) et (N,P,Q), les indices de plans, covariants, étant notés tensoriellement u_i et v_j :

U.V = g^ij u_i v_j

Explicitement :              a* = , et ses permutations circulaires,

                                cos * = , et ses permutations circulaires.

Dans un réseau cubique, le tenseur métrique réciproque se réduit au tenseur unité, divisé par a².

2.6     Application : module ("co-longueur") de covecteurs.

Soit le covecteur (H,K,L), que nous réécrivons sous forme tensorielle u_i.                           (H,K,L) . (H,K,L) = g^ij u_i u_j

Sous réserve que la condition (H, K et L premiers entre eux) ait été respectée, ce résultat est exactement le carré de l'inverse de l'équidistance entre plans de direction (H,K,L). Résultat dont nous avons besoin pour l'application de la loi de Bragg en radiocristallographie.

(H,K,L) . (H,K,L) = g^ij u_i u_j = ,

où d est l'équidistance de plans parallèles, observable en diffraction X ou électronique.

2.7     Angle de droites.

Il se déduit immédiatement du produit scalaire de vecteurs représentant des directions, et des modules de ces vecteurs. On en déduit le cosinus de l'angle entre ces directions :

.cos([u,v,t] , [d,e,f]) = g _ij uⁱ v^j

2.8     Angle de plans.

Il se déduit du produit scalaire de covecteurs représentant des plans, et des modules de ces covecteurs :

On en déduit le cosinus de l'angle entre ces deux plans de coordonnées (H,K,L) et (N,P,Q) :

.cos((H,K,L) ; (N,P,Q)) = g^ij u_i v_j

Les cristallographes interprètent cet angle dièdre comme l'angle de leurs normales, autrement dit, comme angle de vecteurs du réseau réciproque.

2.9     Parallélisme et inclusion de droites dans un plan

Par construction du plan (H,K,L), la droite qui passe par les noeuds [h,0,0] et [0,k,0], est évidemment contenue dans le plan (H,K,L).

Ses indices (coordonnées contravariantes) : [-h,k,0], ou équivalent [h,-k,0].

Par permutation circulaire, on peut en dire autant des droites [0,k,-l] et [-h,0,l]. Toutes les droites dont les indices sont combinaisons linéaires de deux quelconques de ces trois triplets, sont aussi incluses dans ce plan.

Il n'y a besoin d'aucune hypothèse métrique, pour constater la condition de parallélisme droite-plan :

[-h,k,0].(H,K,L) = hH - kK = M - M = 0

C'est bien un produit scalaire entre coordonnées naturelles d'un covecteur (covariantes), et coordonnées naturelles d'un vecteur (contravariantes), qui peut donc s'exprimer sans le truchement du tenseur métrique.

On peut poursuivre la vérification pour toutes les combinaisons linéaires :

( [-h,k,0] + [0,-k,l] + [h,0,-l]).(H,K,L) = (-hH+kK) + (-kK+lL) + (hH-lL) = 0, pour tout , et réels.

Le résultat est général : [u,v,t].(H,K,L) = 0       <==>   [u,v,t] // (H,K,L).

2.10   Angle de droite et plan.

On sait que quand l'angle est nul : [u,v,t].(H,K,L) = 0   <==>   [u,v,t] // (H,K,L)

Expression complète : on n'a besoin du tenseur métrique que pour les longueurs des vecteurs. On prend le plan de coordonnées (H,K,L), et la droite de coordonnées [d,e,f], notés tensoriellement : u_n , et vⁿ .

.sin((H,K,L) , [d,e,f]) = u_n vⁿ

Car le tenseur métrique en coordonnées mixtes, se réduit au symbole de Kronecker.

2.11   Direction d'arête intersection de deux plans.

Etant donnés deux plans de coordonnées (H,K,L) et (N,P,Q), leur arête de coordonnées [u,v,t] répond aux deux équations :                         [u,v,t].(H,K,L) = 0

                                      [u,v,t].(N,P,Q) = 0

Pour vérifier que ces deux plans ne sont pas parallèles, formons le produit extérieur de leurs coordonnées :

D = (H,K,L) ^ (N,P,Q) = 0.

Si les coordonnées de ne sont pas toutes nulles, le problème n'a qu'une seule direction solution. Cette solution vérifie alors l'équation : . [u,v,t] = 0

Si parmi les coordonnées strictes de , seul HP-KN n'est pas nul, on voit qu'obligatoirement u = v = 0. Ce qui donne l'arête [0,0,1].

Ceci nous incite à proposer une solution pour la coordonnée t :

t = (HP - KN).              Il ne nous reste alors plus de choix, il vient immédiatement :

u = (KQ - PL)

v = (LN - HQ)

Réécrivons selon cette solution : = . 

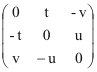Pour obtenir la contravariance, prendre = V, volume de la maille de base.

2.12   Définition d'une direction de plan par deux vecteurs non colinéaires.

Soient [u,v,t] et [d,e,f] les coordonnées de ces vecteurs. On a à résoudre un système de deux équations :

[u,w,t].(H,K,L) = 0

[d,e,f].(H,K,L) = 0

On forme le produit extérieur de ces vecteurs, et on obtient une solution 2-contravariante :

H' = wf - et,                                K' = td - fu,                    L' = ue - dw

[u,w,t] ^ [d,e,f] ₌

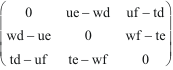
Autrement dit, on prend la matrice 3 × 2 : , et on calcule ses trois mineurs : .

Il reste alors à convertir ou utiliser notre résultat de type (2, 0), qui pour l'instant, ne représente que les coordonnées strictes d'un bivecteur, ou gyreur étendu. Pour obtenir une expression covariante, il faut diviser par une quantité 3-contravariante, typiquement le volume du parallélépipède défini par les (3) vecteurs de la base courante : V= e₁ ^ e₂ ^ e₃. Autrement dit, le déterminant des coordonnées de e₁, e₂, e₃. D'où les coordonnées d'équiplan (de direction de plan) covariantes :

H = (wf - et)/V.                          K = (td - fu)/V.                           L = (ue - dv)/V.

2.13   Vraies et fausses équivalences.

On a vu qu'une direction de plan, autrement dit un équiplan, peut être défini aussi bien par un covecteur, que par un gyreur. En effet, l'équiplan contient MOINS d'informations que le covecteur, ou que le gyreur.

Mais le gyreur n'est en aucune façon équivalent au covecteur : ils contiennent des informations différentes, impossibles à connecter de façon intrinsèque.

Le covecteur (p, q, r) représente naturellement un vrai plan. Ce plan est le noyau de l'application linéaire de R³ vers R : [x,y,z] -----> (p,q,r).[x,y,z] - 1. Ceci définit où est ce plan, par rapport à l'origine du repère .

Un gyreur strict unitaire représente une projection dans un plan, et un quart de tour dans ce plan.

Un gyreur étendu représente une aire dans un équiplan, orientée par le sens de parcours de son périmètre, dans une direction de plan. Il ne dit rien de l'emplacement de cette aire, ni de son éventuelle forme.

Mais pour oser affirmer aux étudiants, ainsi que le font certains physiciens, que le gyreur étendu, et le covecteur, c'est kif-kif, ou "dual", il faut sacrément se dispenser de l'épreuve de réalité abstraite - mathématicienne, et de l'épreuve de réalité concrète - physicienne. Dans les deux paragraphes précédents, nous avons calculé les coordonnées de l'un depuis l'autre, mais à une constante multiplicative arbitraire près, irrémédiablement arbitraire, irrémédiablement dépourvue de signification physique. Nous ne cherchions que la direction de plan.

3     Gyreurs unitaires. Approche sur bases orthonormales.

Se reporter si nécessaire à l'annexe algébrique : matrices qui commutent; matrices qui anticommutent.

Nous nous limiterons dans ce chapitre, aux dimensions 2 et 3. Les applications et extensions en dimension 2 complexifiée, et en dimension 4 réelle ou complexifiée, sont toutes reportées deux chapitres plus loin.

3.1     Génération en dimension 2.

En dimension deux, on en sait les deux seules formes possibles : = J, et son opposé = -J.

On sait depuis Hamilton, que cette matrice réalise le nombre imaginaire i (ou j en électricité).

Ce gyreur J est invariant dans toute rotation du plan, de matrice , dont il est justement l'opérateur infinitésimal. J et -J ont le même déterminant, de valeur +1.

On connaît la formulation classique, pour toute matrice de rotation : = exp( J).

Explicitons les valeurs propres et les directions propres ("vecteurs-propres", ou plus correctement, vectoroïdes propres ) de la matrice J :

 . = , ou . = = 0.

Le polynôme ( ² + 1) est le polynôme caractéristique de cette application linéaire.

Ses racines sont dans le domaine complexe : = i, d'où x = i, y = 1, et = - i, d'où x = 1, y = i. Les vectoroïdes-propres, dans l'espace C², sont de module nul, et sont classiquement appelés "vecteurs isotropes".

Dans la base propre (du complexifié), , , J prend donc la forme diagonale : , et le tenseur métrique (carré hermitien de la matrice de changement de base, multiplié par l'unité d'aire) est inchangé : . = .

Quant à la matrice de rotation exp( J), de polynôme caractéristique ( ² + 1 -2 cos ), ses valeurs propres sont = cos ± i.sin , et elle a les mêmes vectoroïdes-propres : x = i, y = 1, et son conjugué (sauf cas où est nul, alors tout vectoroïde réel est vectoroïde-propre).

Ses invariants classiques : trace = Jⁱ_i = 2 cos , déterminant = J¹₁ .J²₂ -J²₁ .J¹₂ = 1.

En dimension 2, il n'y a pas à distinguer le gyreur, de la rotation d'un quart de tour.

Remarque. Il est intéressant de comparer les rotations avec les symétries laissant une droite invariante.

Matrice de symétrie autour d'une droite d'indices [cos ; sin ] :                    S = .                               

Son polynôme caractéristique : (1- ²), de racines opposées +1 et -1.            S² = .

Invariant d'ordre 1 (trace) = 0,                             Invariant d'ordre 2 (déterminant) = -1.

Depuis Olinde Rodrigues, et E. Cartan , il est classique de remarquer que toute rotation d'angle = -  est aussi le produit de deux symétries, dont les droites invariantes font entre elles un angle de /2 :

. = .

Soit une symétrie autour de la droite d'indices [cos( /2); sin( /2)], suivie d'une symétrie autour de la droite [cos( /2); sin( /2)].

En particulier pour la rotation d'un quart de tour : = 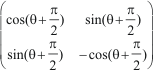. . Avec le choix = 0, on obtient deux matrices de réflexion de Pauli : = . .

Multiplions ce résultat par i, et l'on obtient la seconde matrice de Pauli : i . = = ₂ .

₁ = est une matrice de réflexion autour de la droite d'indices [1; 1].

  ₃ = , autour de la droite d'indices [1; 0] ; et ₂ = est une matrice de réflexion autour d'une droite isotrope, d'indices [1; i].

3.2     Génération en dimension 3.

En dimension trois, et plus, un gyreur unitaire est décomposable en une projection sur le plan stable, suivie ou précédée, d'une rotation d'un quart de tour dans le même plan stable. Il est remarquable que ces opérations commutent. Le groupe de ces rotations en dimension 3, est usuellement appelé SO(3).

3.2.1   Les matrices de projections de base.

Limitons-nous provisoirement aux projection intérieures sur les équiplans de base :

En repère orthonormé :  P_xy = . P_zx = . P_yz = .

Polynôme caractéristique de P_xy : 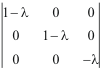= - (1- )², de racines 0, et 1 (double). Ce sont les valeurs propres de cette matrice. L'équiplan invariant a pour covecteur directeur (0,0,1). L'équidroite noyau (préimage de zéro), a un vecteur directeur d'indices [0,0,1].

En toute base, tout projecteur intérieur sur un équiplan a pour polynôme caractéristique : (1- )². Tout projecteur est idempotent : P² = P. Et sauf s'il s'agit de la projection triviale, l'identité, sa matrice n'est pas inversible.

3.2.2   Les matrices de rotations de base

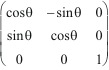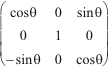R_xy( ) = . R_zx( ) = . R_yz( ) = .

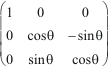Connaissons mieux cette rotation, de matrice R_xy( ) = .

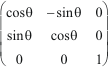Son équation caractéristique, dont les racines sont valeurs propres :

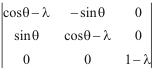 = - ³ + (2cos + 1) ² - (2cos + 1) + 1 = (1- ) . ( ² - 2 cos + 1).

Les invariants d'une matrice carrée, et par extension d'un tenseur de valence nette nulle, sont les coefficients de son équation caractéristique, multipliés par (-1)^{degré de}  .

Ordre d'un invariant : le degré des produits de coefficients, dont il est la somme homogène.

La somme : (ordre de l'invariant) + (degré du terme en ) = dimension de la matrice carrée.

Les trois invariants de la matrice de rotation (pas d'invariant d'ordre nul) :

Invariant d'ordre 1 (trace) = 2 cos +1,                              Invariant d'ordre 3 (déterminant) = 1.

Invariant d'ordre 2 (somme des mineurs diagonaux) : + + = 2cos + 1.

Remarque. Propriété caractéristique des matrices de rotation de R³ : leurs 1er et 2e invariants sont égaux.

Cela les oppose aux symétries par rapport à un plan (anti-déplacements).

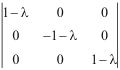  = -(1- )².(1+ ) = - ³ + ² + - 1 .

Invariant d'ordre 1 (trace) = 1,                             Invariant d'ordre 3 (déterminant) = -1.

Invariant d'ordre 2 = + + = -1.

Toute rotation d'angle  = -  est aussi le produit de deux symétries, dont les plans invariants font entre eux un angle de  /2 : . = .

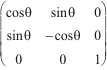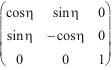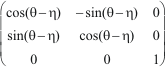Valeurs propres, directions propres.

Les valeurs propres de la matrice de rotation R_xy( ), sont = 1, et = cos ± i.sin ( et ). Ses vectoroïdes-propres appartiennent à C³ : , , et , dont le premier et le second sont isotropes.

Sauf si est nul, auquel cas tout vecteur (ou vectoroïde arbitraire) réel est vectoroïde-propre.

Les rotations sur E₃ (espace affine à R³), sont isomorphes avec le groupe multiplicatif des quaternions unitaires, ce qui a mystifié tout le monde de 1843 jusque vers 1901. Pour raisons algébriques, certains préfèrent utiliser deux fois le quaternion d'angle moitié . Mais cela ne divise pas la mystification par deux.

Remarque : Si est infinitésimal, les valeurs propres ne diffèrent que d'un infinitésimal :

 = 1 et = 1 ± i d

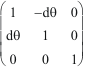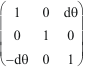 Donc les trois matrices R_xy( ) = . R_zx( ) = . R_yz( ) = 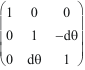, commutent, à l'infinitésimal du second ordre près d² . C'est ce qui justifie l'usage des gyreurs.

Attention ! Les matrices R_xy( /2), R_yz( /2) et R_zx( /2), munies de la multiplication matricielle simple, ne sont pas une réalisation de l'algèbre des quaternions. En effet, la transformation qui réalise l'algèbre des quaternions est différente, c'est le changement de base :  R_xy( /2) . R_yz( /2) . R_xy^-1( /2) = R_zx( /2).

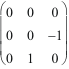
3.2.3   Gyreurs : formes de base, dans les trois équiplans de base :

sur yOz : J_yz = = . = . ,

sur zOx : J_zx = ,                       et sur xOy : J_xy = .

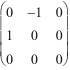De là, on obtient par combinaisons linéaires, le groupe additif des gyreurs. Pour le sous-ensemble des gyreurs unitaire, on l'obtient par les rotations et symétries à trois dimensions d'un tel gyreur pris dans un plan quelconque. Leurs matrices représentatives ont toutes les mêmes valeurs propres : 0, i et -i. Les vectoroïdes propres, dans un plan de l'espace C³, sont de modules euclidiens nuls, et sont qualifiés : vecteurs isotropes.

Le sous-espace orthogonal au plan stable, est noyau (préimage de zéro) de l'application J_kl : valeur propre nulle.

Leurs équiplans stables ont respectivement pour coordonnées covariantes : , , et .

Familiarisons-nous avec les combinaisons des gyreurs dans deux plans de base, sans le troisième.

Un gyreur est invariant par rotation dans son équiplan stable, ici xOy.

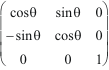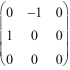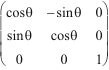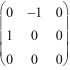 . . = = J_xy = R_xy(- ). J_xy .R_xy( ).

J_xy est l'opérateur infinitésimal de la rotation R_xy( ) : J_xy= .

Il est classique de remarquer que cette matrice est une exponentielle de matrice : R_xy( ) = exp ( J_xy).

On peut donc réécrire ce résultat : exp (- J_xy) . J_xy . exp ( J_xy) = J_xy.

Quels sont les trois invariants d'une quelconque des matrices J_kl ?           trace nulle.

Second invariant égal à l'unité : = 1.                   Déterminant nul. Une matrice de gyreur est donc de rang 2.

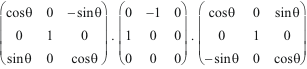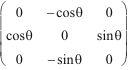 = = cos . J_xy - sin . J_yz .

exp (- J_zx) . J_xy . exp ( J_zx) = cos . J_xy - sin . J_yz.

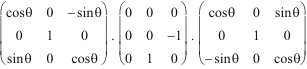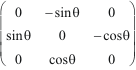 = = sin . J_xy + cos . J_yz.

exp (- J_zx) . J_yz . exp ( J_zx) = cos . J_yz + sin . J_xy.

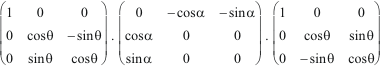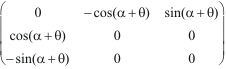 = . Nous avons redécouvert la formule de Moivre !

Voici le cas général, auquel plusieurs autres formes sont équivalentes :
= .

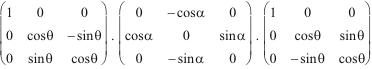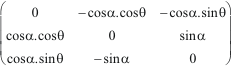On a bien le cas général : un gyreur sur R³ n'a que 3 composantes strictes.

Pour un gyreur unité, seuls deux paramètres, sont libres. Prenant les angles en coordonnées sphériques, avec longitude, et latitude, on peut toujours ramener ces composantes strictes à : sin , cos .cos , et cos .sin .

Seul l'invariant d'ordre 2 est non nul : (sin )² + (cos .cos )² + (cos .sin )² = (sin )² + (cos)² = 1 .

Trace nulle. Déterminant nul. Une matrice de gyreur est toujours de rang 2.

Diagonalisation : Tout comme les trois rotations de base, les trois gyreurs de base ne sont pas simultanément diagonalisables, sinon ils commuteraient entre eux.

Jyz prend la forme: sur la base 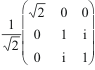. Jzx prend la forme: sur la base 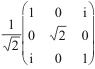. Jxy prend la forme: sur la base .

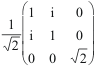Il est évident que ces trois bases ne coïncident pas du tout. Il faut choisir le plan stable de diagonalisation.

Les matrices de gyreurs sur R³ ne forment pas un groupe multiplicatif.

-Jyz² =            Jyz. (-Jyz) = = Pint(Jyz) : projecteur sur le plan stable de Jyz: yOz.

D'où le développement en série de l'exponentielle, et : exp ( J_yz) = Pext(J_yz) +sin .J_yz +cos .Pint(J_yz).

Et les relations similaires sur J_zx et J_xy donnent de même les projecteurs sur leurs plans stables.

Jyz. Jzx = .                                            Jzx. Jyz = .  

Jyz. Jzx . = .                            Jzx. Jyz . = .               Une projection sur un axe, et un quart de tour.

Jzx. Jxy = .                                            Jxy. Jzx = .

Jxy. Jyz = .                                            Jyz. Jxy = .

Nous exploiterons ces résultats, pour définir le produit biscalaire (contracté deux fois) de deux gyreurs.

Ce sont les conséquences d'un noyau de dimension 1 pour tout gyreur de E₃ (espace affine à R³), autrement dit, qu'un gyreur résulte de la composition d'une rotation d'un quart de tour, et d'une projection plane.

On remarque les commutateurs, ou produits antisymétriques :   [J_yz, J_zx ] = J_yz . J_zx - J_zx . J_yz = J_xy.

                                                                                                      [J_zx, J_xy ] = J_zx . J_xy - J_xy . J_zx = J_yz.

                                                                                                      [J_xy, J_yz ] = J_xy . J_yz - J_yz . J_xy = J_zx.

La possibilité de définir ces produits antisymétriques de gyreurs stricts, découle immédiatement de la composition des rotations. On ne l'a ici démontrée que pour le cas particulier des bases orthonormales.

On peut envisager d'écrire cela en cross-product : J_xy.= J_yz × J_zx , et de le prononcer "produit gyratoriel". C'est le seul cas où un cross-product devient correct et cohérent : strictement entre gyreurs.

L'extension éventuelle aux gyreurs physiques, physiquement dimensionnés, exige de vérifier le respect des règles de covariance tensorielle, et de cohérence dimensionnelle.

3.2.4   Extensions du commutateur en mécanique quantique.

Représentation régulière des opérateurs de moment angulaire orbital , à la dimension physique près :

1 i . Jyz = i . ,               2 i . Jzx = i . ,                 3 i . Jxy = i . .

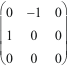Les commutateurs de ces opérateurs hermitiens abstraits réalisent une algèbre ressemblant à celle des matrices de Pauli : [₁; ₂] = -[J_yz, J_zx ] = -J_yz . J_zx + J_zx . J_yz = -J_xy = i ₃.

4     Conclusion provisoire.

Dans la suite de l'article, consacrée à la métrique des gyreurs, nous établirons l'écriture la plus générale du module d'un gyreur; nous la vérifierons dans un exercice en base non orthonormale. Nous établirons le passage de l'expression d'un gyreur, à l'équation de son plan stable. Nous en déduirons la projection intérieure et la projection extérieure sur un gyreur. Nous en déduirons le produit biscalaire de deux gyreurs. C'est indispensable pour établir la densité volumique d'énergie magnétique, et notamment pour commencer d'établir la théorie des spectres de limailles de Faraday, qui exigent des champs inhomogènes. A expérience facile, interprétation et théorie nettement plus délicates. Nous terminerons par les extensions en dimension quatre, et notamment dans l'espace-temps de Minkowski.

Ainsi, nous aurons développé le calcul sur les êtres plans, tels que les gyreurs, et sur leurs relations avec les êtres vectoriels. Tous calculs géométriques nécessaires à la physique élémentaire. Cela dégage un chemin bien plus économique entre la physique élémentaire enseignable dans les lycées, et la vraie physique théorique.

Ici encore, nous avons recueilli les fruits du travail de désengorgement sémantique précédent. Jusqu'à présent, il était abusivement difficile de deviner à la lecture d'un physicien, laquelle au juste des acceptions admises, il voulait écrire, quand il écrivait une expression "vectorielle". Notamment, l'usage du monôme dimensionnel, et de l'analyse dimensionnelle, était terriblement handicapé par l'accrochage de la communauté des physiciens à des incorrections mathématiques, physiquement injustifiables. Accepter l'outil mathématique adéquat permet de grandes clarifications, qui ne font que commencer. Ce sera alors à vous de jouer.

Notes :

1                         L'habitude est incorrecte, d'appeler "tenseur", la suite de coordonnées qui exprime un tenseur, relativement à une base.

2                         D. Béklémichev; Cours de géométrie analytique et d'algèbre linéaire. Editions Mir. Moscou. 1984.

3                         R. Penrose, W. Rindler. Spinors and space-time. Vol. 1: Two-spinor calculus and relativistic fields. Cambridge 1984.

4                          En analyse des contraintes, le tenseur des contraintes usuel viole les règles de variance: on y repère un élément de surface par un seul indice, au lieu de deux. C'est que cette surface est représentée par un covecteur, multiplié par un volume non orienté. Cette convention discutable est très ancrée dans les habitudes. Nous y reviendrons. 

5                       Les techniques matricielles sont appliquables à tout espace vectoriel général. Les directions propres contiennent donc des vectoroïdes propres. Ici tous nos exemples sont pris dans l'espace euclidien ordinaire, et nos cibles sont le plus souvent de vrais vecteurs, ou de vrais covecteurs.

6                        E. Cartan. The Theory of Spinors. Dover 1981, Hermann 1977. Paris 1937.

7                        R. Saint-Guilhem; Notions fondamentales de mathématiques modernes. T1. Ellipses. Paris 1989.

8                        W. Greiner, B. Müller; Quantum Mechanics Symmetries. Springer, Berlin 1989.