Des grandeurs qui ne sont pas vectorielles : les gyreurs.. 1

Pour ne plus violer la syntaxe géométrique de la physique. 1

Auteur : Jacques Lavau  1

0 . 1 .               Prérequis. 1

1 .        Le besoin en physique : le quart-de-tour entre deux vecteurs. 1

1 . 1 .               En cinématique, description du mouvement circulaire : 1

1 . 2 .               Moment d'une grandeur vectorielle. 2

1 . 3 .               Electricité : Loi d'Ampère-Laplace. 2

1 .4 .     Loi de Biot et Savart, 3

1 . 5 .               Loi de l'induction électromagnétique  4

2 .  Quelles grandeurs physiques ont la nature géométrique de gyreurs ?  4

2 . 1 .               gyreurs stricts : 4

2 . 1 . 1 .          Vitesse angulaire, en rad/s      [R.T^-1] 4

2 . 1 . 2 .          Accélération angulaire, en rad/s²     [R.T^-2] 4

2 . 1 . 3 .          Champ magnétique       [M.T^-1.Q^-1.R^-1], 4

2 . 2 .               gyreurs étendus : 5

2 . 2 . 1 .          Vitesse aréolaire, en m².rad/s     [R.L².T^-1] 5

2 . 2 . 2 .          Moment d'une force, ou d'un couple, en J/rad   [M.L².T^-2.R^-1] 5

2 . 2 . 3 .          Moment angulaire (et spin), en J.s/rad    [M.L².T^-1.R^-1] 5

2 . 2 . 4 .          Flux magnétique (circulation de le long du bord de la surface) [M.L².T^-1.Q^-1.R^-1] 5

2 . 2 . 5 .          Moment magnétique d'un aimant; d'une particule.  [R.L².T^-1.Q], 5

2 . 3 .               Densités volumiques de gyreurs étendus : 5

2 . 3 . 1 .          Densité volumique de moment angulaire.    [M.L^-1.T^-1.R^-1] 5

2 . 3 . 2 .          Densité volumique de moment magnétique : le champ = /µ : [R.L^-1.T^-1.Q]. 5

2 . 4 .               Cogyreurs étendus : 5

2 . 4 . 1 .          Vitesse anti-aréolaire :      [R.L^-2.T^-1] 5

2 . 5 .               Leurs relations entre eux ?  5

3 .        Rappel : quelles sont les grandeurs physiques qui sont vectorielles ?  5

4 .        Rappel : interprétation géométrique des nombres complexes. 6

4 . 1 .               Addition des nombres complexes : interprétation  6

4 . 2 .               La multiplication des nombres complexes ?  6

4 . 3.     Ces deux interprétations sont fascinantes, mais contradictoires... 6

4 . 4.     Image complexe du produit scalaire. 7

5 .        Hamilton a voulu faire mieux : dans l'espace tridimensionnel. 7

5 . 1 .               Quand Hamilton s'emmèle (1805-1865). 7

5 . 2 .               Le produit "vectoriel" : fausse solution à un vrai besoin. 8

6 .        Un gyreur opère la partie infinitésimale d'une rotation infinitésimale. 9

6. 1.      gyreur strict : opérateur associé à une rotation infinitésimale stricte, 9

Sténo graphique du gyreur strict en relation avec deux vecteurs. 9

6 . 2 .               Gyreur étendu (ou bivecteur) : opérateur d'inertie en rotation. 9

Sténo graphique du gyreur étendu, en relation avec deux vecteurs. 9

6 . 3 .               Densité volumique de gyreur étendu. 10

6 . 4 .               Tables de multiplication EXTERNES : 10

6 . 5 .               Associativité : rang trois. 10

6 . 6 .               Une grandeur gyratorielle, c'est un gyreur, éventuellement multiplié par d'autres unités physiques non géométriques. 10

7 .        Trois traditions. 10

7 . 1 .               Tradition tout-vecteur : Hamilton (1843), Clerk Maxwell (1873), Heaviside (1893) 10

          C'est un bâton, et ça tient sur une droite. 11

          Ça ne tourne plus, ça court le long de la droite. 11

Descendance oubliée : les dyadics de Josiah Willard Gibbs (1839-1903). 11

7 . 2 .               Tradition universitaire minoritaire (depuis Pierre Curie ? 1894 ?). 11

          Au moins, ça tourne, dans le même sens que le phénomène physique. 11

          Une seule erreur : c'est un bâton, dit "vecteur axial". 11

7 . 3 .               Manière correcte : H. Grassmann 1844, G. Peano 1888, H. Weyl 1918, A. Einstein 1921, E. Cartan, J. Barbotte 1948. 11

          Ça tourne, 11

          C'est dans un plan. 11

8 .        Symétries comparées. 12

9 .        Coordonnées d'un gyreur, en repère orthonormé. 12

9 . 1 .               Cas du gyreur strict, quotient. 12

9 . 2.     Calcul rigoureux. 12

9 . 3 .               Calcul simplifié. 13

9 . 4 .               Cas du gyreur étendu, produit extérieur. 14

9 . 5 .               Exercice. Utiliser le produit extérieur en quotient : 14

10 .      Syntaxe algébrique et géométrique. 14

Comment corriger les anciens produits "vectoriels" de vos manuels. 14

10 . 1 .              Cas 1 : Produit extérieur de vecteurs = gyreur étendu. 15

10 . 2 .              Cas 2 : Un gyreur multiplie un vecteur = un vecteur perpendiculaire. 15

10 . 3 .              Cas 3 : Quotient extérieur de vecteurs = gyreur strict. 15

1.         Position dans le livret de famille. 15

11 . 1 .              Difficulté réelle : moment angulaire et moment d'inertie. 15

11 . 2 .              Difficulté peu utile : le théorème d'Ampère  16

11 . 3 .              Le rotationnel, ou dérivée extérieure d'un champ tensoriel (d'ordre non nul). 16

11 . 3 . 1 .         Cas historique : rotationnel d'un champ vectoriel : = = 16

11 . 3 . 2 .         Cas général de la dérivation extérieure, en dimension n. 17

11 . 4 .              Les équations de Maxwell, débarbouillées par Einstein en 1921. 17

12 .      Prochaines actions, et moralité. 17

Auteur : Jacques Lavau  17

Des grandeurs qui ne sont pas vectorielles : les gyreurs.

Pour ne plus violer la syntaxe géométrique de la physique.

Auteur : Jacques Lavau

0 . 1 .  Prérequis.

La leçon sur les bipoints, les vecteurs, projection intérieure et projection extérieure.

Repérer un point par ses coordonnées sur un repère. Projeter un point sur les axes du repère. Les translations dans le plan ou l'espace. Le sinus et le cosinus d'un angle.  L'angle d'une droite et d'un plan.

Les nombres complexes ne sont nécessaires que pour comprendre le rappel des erreurs historiques.

1 .     Le besoin en physique : le quart-de-tour entre deux vecteurs.

Un petit nombre de lois physiques expriment qu'une grandeur vectorielle est perpendiculaire à une autre. Il faut projeter dans un plan de direction donnée, puis faire un quart de tour dans ce même plan, pour tracer le second vecteur, puis le multiplier par une grandeur physique scalable précise. L'étude du bref inventaire exhaustif de ces lois, vérifie qu'elles expriment toutes la partie infinitésimale d'une rotation infinitésimale :

1 . 1 .  En cinématique, description du mouvement circulaire :

Et la vitesse angulaire est bien constante, pour un mouvement de rotation uniforme.

L'accélération centripète γ s'exprime par le produit de la vitesse périphérique, par la vitesse angulaire:

= Où relie deux vecteurs orthogonaux.

Ce genre de dessin de connexion se retient facilement, car il ressemble à une courroie qui passe sur des poulies. Il ne signifie pas "poulies et courroie" !  Il signifie une connexion géométrique entre trois grandeurs vectorielles, et la grandeur Ces quatre grandeurs physiques sont dans un même plan.

Définition : les grandeurs physiques qui ont la propriété de faire faire un quart de tour à une grandeur vectorielle, pour donner une autre grandeur vectorielle, sont dénommées des gyreurs.

Avant d'avoir défini mathématiquement la nature géométrique de la grandeur vitesse angulaire, nous avons du moins établi que nous en avons besoin, et quelles sont ses propriétés exigées. C'est un cahier des charges. Il est correct de définir comme le quotient de la vitesse périphérique par le rayon vecteur du point matériel, et aussi comme le quotient de l'accélération centripète par la vitesse périphérique.

1 . 2 .  Moment d'une grandeur vectorielle.

En mécanique, le moment d'une force, réclame un être géométrique légèrement différent, car là il s'agit du produit d'un vecteur par la projection extérieure de l'autre, et non plus de leur quotient. Applications : balance à fléau, balance Roberval, engrenages, poulies, leviers, etc...

Ce produit extérieur[2], utilise le sinus de l'angle des vecteurs, et a été inventé en 1844 par Hermann Grassmann (1809-1877). Son résultat a été dénommé un bivecteur par E. Cartan[3]. Nous préférons le dénommer "gyreur étendu". Deux bivecteurs sont équivalents s'ils appartiennent à la même direction de plan, qu'ils ont même aire, et tournent dans le même sens autour de cette aire. Cette relation d'équivalence, est la réplique fidèle de l'équipollence des bipoints, définissant l'égalité des vecteurs. Cette partie mathématique a été correctement exposée par Postnikov[4]. Le sinus est une fonction impaire : (sin(-x) = -sin x), donc le produit extérieur est anticommutatif :     V1 V2 = - V2 V1.  On dit aussi que cet opérateur "^" est antisymétrique.

Ce produit extérieur, dont le résultat est un gyreur étendu, représente bien une troisième loi de la mécanique : la loi de conservation du moment angulaire, produit extérieur du rayon vecteur par l'impulsion.[5]

1 . 3 .  Electricité : Loi d'Ampère-Laplace.

Prenons un électron, lancé dans le vide d'un tube de téléviseur, ou d'un magnétron, ou d'un microscope électronique. Il est lancé avec une vitesse v, et rencontre un champ magnétique B (qui a la nature géométrique d'un gyreur).

 Cas particulier : le plan du champ magnétique est bien parallèle au vecteur vitesse de l'électron. Le champ dévie alors l'électron dans une trajectoire circulaire. L'impulsion communiquée à l'électron par le champ magnétique reste alors toujours perpendiculaire à la vitesse, et le module de la vitesse ne change pas.

 Cas général : La trajectoire est hélicoïdale, avec la section circulaire de l'hélice dans la direction de plan du champ magnétique. Le champ n'agit que sur la projection intérieure de la vitesse sur le plan stable de La projection extérieure de la vitesse est inchangée, et donne l'axe de la trajectoire hélicoïdale.

 Pour un conducteur parcouru par l'intensité i :

=             (Loi d'Ampère-Laplace).

Signification physique du signe moins : deux courants de sens contraire se repoussent, de même sens s'attirent (c'est la loi qui donne la définition légale de l'ampère). Le champ est celui produit par les autres éléments de courant.

1 .4 .   Loi de Biot et Savart,

donnant le champ en fonction des circuits et de l'intensité qui les traverse. D'abord, on va se contenter d'en donner le sens, en fonction du sens des courants.

Ces trois derniers schémas sont dus à Pierre Léna, vers 1964. Académicien depuis.

Le produit extérieur est indispensable. En France, le gros des troupes physiciennes le confond avec le "produit vectoriel", qui, en France exclusivement, emprunte la même apparence d'écriture. Cette apparence d'identité d'écriture est due à un piratage purement français : les mystificateurs du "produit vectoriel" ont piraté l'écriture de l'algèbre extérieure, avec un "^" pour se masquer dessous, au lieu de leur "x" originel[7]. Dans les pays anglo-saxons, le "produit vectoriel", "cross-product" a gardé son " x ", et qui veut se repérer le peut encore. Chez nous, la privation de repères est la règle, et la confusion règne[8].

La forme de la loi de Biot et Savart appelle quelques simplifications. La projection anti-extérieure apporte-t-elle la solution ? = . Mais on peut trouver le dénominateur disgracieux.

La simplification est plus convainquante, en exprimant cette loi sous forme vectorielle, avec le potentiel vecteur = = , et =

Enfin, on réunit les deux lois : Ampère-Laplace, et Biot et Savart, en exprimant l'énergie d'interaction de 2 particules chargées : .

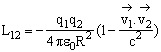Attention, cette formule ne respecte pas l'invariance relativiste.

1 . 5 .  Loi de l'induction électromagnétique

Cette loi devient bien plus sympathique, quand on l'exprime sous forme vectorielle :

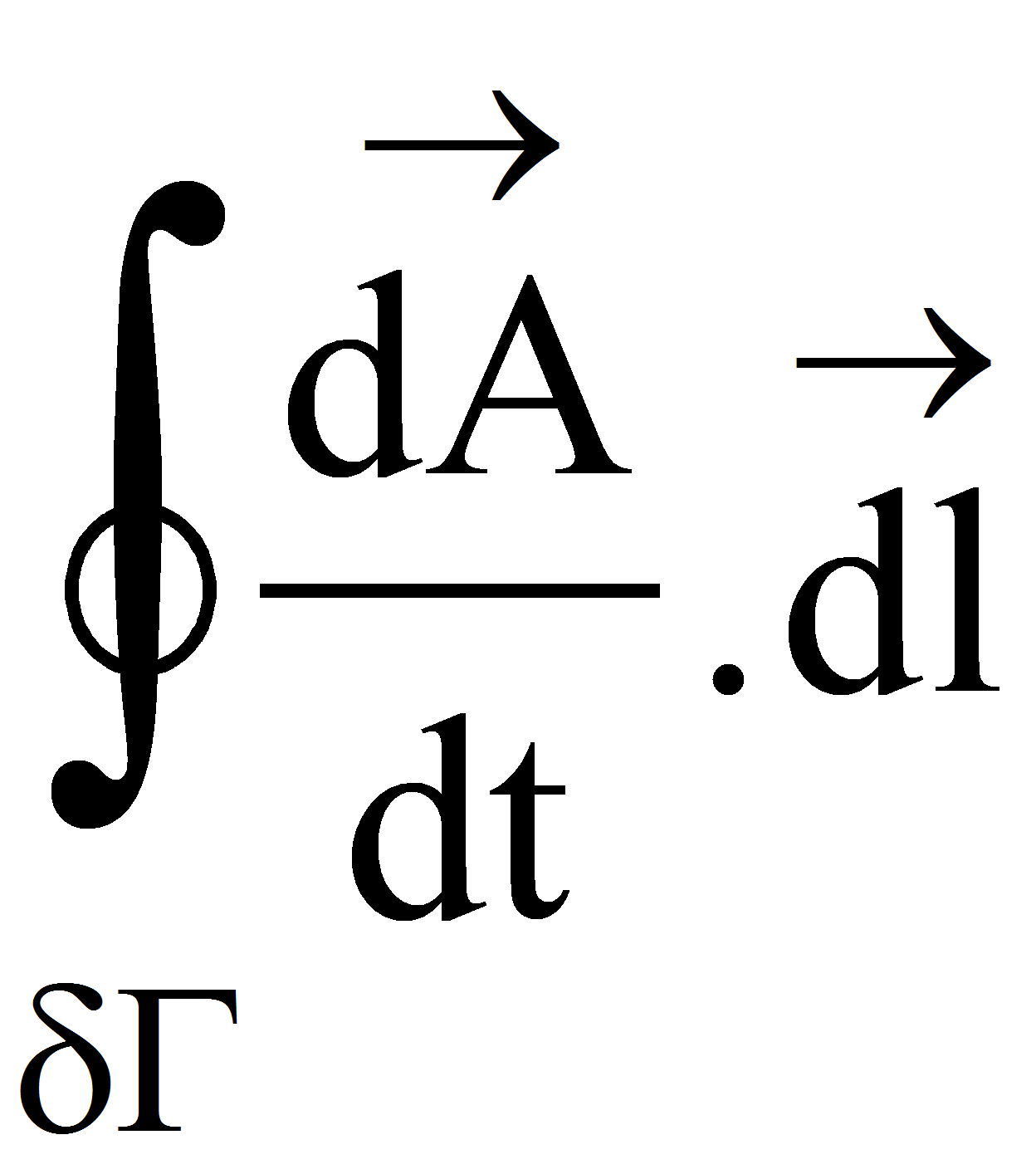= - ssous forme intégrale, d'où localement : = - -

où φ est le potentiel scalaire de l'électrostatique. Le potentiel vecteur est un grand mal aimé de l'enseignement, du moins tant qu'on n'aborde pas la mécanique quantique, qui, elle, ne saurait s'en passer. Pourtant, regardez comme le lagrangien d'une particule dans un champ électromagnétique, est simple : . Cette expression simplifiée est valide pour des vitesses faibles devant la célérité de la lumière c. Pour toute trajectoire réelle, est stationnaire (minimale le plus souvent), et de plus, multiple entier du quantum d'action h, de Planck : 6,626 . 10^-34 joule . seconde par tour.

2 .  Quelles grandeurs physiques ont la nature géométrique de gyreurs ?

Toutes sans exception font intervenir la partie infinitésimale d'une rotation infinitésimale, donc une différenciation antisymétrique. Nous y reviendrons plus loin avec la définition du rotationnel. La lettre R dans l’expression dimensionnelle désigne le radian : quotient de deux vecteurs perpendiculaires de même module.

2 . 1 .  Gyreurs stricts :

Quotients de deux vecteurs, ils n'ont pas de longueur dans leur dimension physique.

2 . 1 . 1 .          Vitesse angulaire, en rad/s                                                              [R.T^-1]

2 . 1 . 2 .          Accélération angulaire, en rad/s²                                                     [R.T^-2]

2 . 1 . 3 .          Champ magnétique ( )                                                 [M.T^-1.Q^-1.R^-1],

en joule-seconde, par mètre carré, par radian, et par coulomb, ou tesla.

2 . 2 . Gyreurs étendus :

Produits extérieurs de deux vecteurs, ils ont le carré de la longueur, dans leur dimension physique.

2 . 2 . 1 .          Vitesse aréolaire, en m².rad/s                                                      [R.L².T^-1]

2 . 2 . 2 .          Moment d'une force, ou d'un couple, en J/rad                   [M.L².T^-2.R^-1]

2 . 2 . 3 .          Moment angulaire (et spin), en J.s/rad                               [M.L².T^-1.R^-1]

2 . 2 . 4 .          Flux magnétique ( = circulation de le long du bord de la surface) [M.L².T^-1.Q^-1.R^-1]

2 . 2 . 5 .          Moment magnétique d'un aimant; d'une particule.          [R.L².T^-1.Q],

ou vitesse aréolaire de charge électrique, en radian-coulomb-mètres carrés par seconde.

2 . 3 .  Densités volumiques de gyreurs étendus :

2 . 3 . 1 .          Densité volumique de moment angulaire.                        [M.L^-1.T^-1.R^-1]

2 . 3 . 2 .          Densité volumique de moment magnétique : le champ = /µ : [R.L^-1.T^-1.Q].

c'est aussi une densité volumique de vitesse aréolaire de charge électrique, en radian-coulomb par mètre et par seconde.

2 . 4 .  Cogyreurs étendus :

Produits extérieurs de deux covecteurs, ils ont le carré de la longueur en dénominateur.

2 . 4 . 1 .          Vitesse anti-aréolaire :                                                              [R.L^-2.T^-1]

Pour mémoire ?

2 . 5 .  Leurs relations entre eux ?

On peut rassembler trois de ces tableaux partiels en un seul, plus compliqué :

Ce tableau-là n'est pas vraiment intéressant. Nous verrons mieux dans l'article consacré aux liens entre la dimension physique et le caractère tensoriel.

3 .     Rappel : quelles sont les grandeurs physiques qui sont vectorielles ?

Toutes font intervenir une translation, généralement infinitésimale.

Presque toutes, dont toutes les fondamentales, ont la propriété que la longueur y intervient à la puissance 1. A la puissance -2, pour les densités volumiques de vecteurs.

Déplacement                                       [L]

Vitesse                                                [L.T^-1]

Accélération                                        [L.T^-2]

Impulsion (quantité de mouvement)       [M.L.T^-1]

Force                                                  [M.L.T^-2]

Champ électrique                                 [M.L.T^-2.Q^-1]    ([L^-2.Q] pour le vecteur courant de déplacement)

Moment dipolaire électrostatique           [L.Q]

Elément de courant                              [L.T^-1.Q]          (C'est le figurant dans la loi de Laplace).

Potentiel magnétique ( )                     [M.L.T^-1.Q^-1]

On peut en faire le tableau synoptique :

Il est facile de voir que le lien entre une grandeur vectorielle et une grandeur gyratorielle, est soit la multiplication extérieure par un vecteur vitesse, ou par un rayon vecteur, soit la division extérieure par une vitesse, ou par un rayon vecteur. Quatre cas possibles, en tout.

4 .     Rappel : interprétation géométrique des nombres complexes.

Entre 1798 et 1843, des mathématiciens et des astronomes ont remarqué, ou inventé les choses suivantes :

4 . 1 .  Addition des nombres complexes : interprétation

L'addition des nombres complexes est isomorphe[9] à l'addition des vecteurs du plan.

Notamment, la partie réelle et la partie imaginaire d'un nombre complexe peuvent représenter les composantes d'un vecteur, sur deux axes orthonormés.

4 . 2 .  La multiplication des nombres complexes ?

La multiplication par 1 représente une identité.

La multiplication par un réel r, représente une homothétie centrée sur l'origine du repère.

La multiplication par i, représente un quart de tour (à gauche).

La multiplication par e^iθ, représente une rotation d'angle θ, comptée dans le sens direct.

La multiplication par reⁱθ, représente une rotation d'angle θ, comptée dans le sens direct, suivie d'une homothétie de rapport r.

Donc maintenant, les vecteurs de base, sont réinterprétés ainsi : 1, comme pas de rotation du tout,

                                                                                          i, comme quart de tour à gauche, dans le plan.

(On remarque qu'adieu espace vectoriel de dimension 2 :  cette table de multiplication définit un groupe fini à 1 générateur, et non 2.).

4 . 3.   Ces deux interprétations sont fascinantes, mais contradictoires...

Alors que la première interprétation résiste à un changement d'axes, par exemple par une rotation de 45°, la seconde interprétation est pulvérisée par une telle transformation. Un vecteur de base de C représente tantôt un vecteur de base, tantôt pas de rotation et tantôt un quart de tour à gauche. Un complexe représentait tantôt un vecteur et tantôt une rotation ! Tantôt des mètres, et tantôt des radians !

La confusion perdure encore aujourd'hui, entre nombre et grandeur : un nombre complexe est un nombre. La multiplication de deux nombres est une opération interne. Un vecteur du plan est une grandeur. La multiplication de deux grandeurs, par exemple de deux vecteurs, est une opération externe. Mais les astronomes de l'époque ne sont pas avisés de cette contradiction sémantique. Leurs excuses : les nombres complexes en tant que substituts sténographiques des outils d'algèbre linéaire propres au plan, restent un puissant moyen de calcul pour la géométrie plane, et les fonctions analytiques sont fascinantes. Inversement, en électricité, où ce sont les nombres complexes qui sont compétents, on aime bien tracer des diagrammes de Fresnel, et diverses extensions spécialisées : diagrammes de Kapp pour les transformateurs, de Behn-Eschenburg pour les alternateurs, de Blondel pour les moteurs, etc.

Ainsi on a oublié d'élucider le mystère de la coïncidence entre le radian de la géométrie, qui est un quotient de deux longueurs égales et perpendiculaires, et le radian des phénomènes périodiques, qui est le quotient de deux grandeurs en quadrature de phase.

4 . 4.   Image complexe du produit scalaire.

Transposant aux nombres complexes l'opération de produit scalaire, nous obtenons ceci :

Si z = re^iθ, et son complexe conjugué = re^-iθ , alors :  r² = 

D'où le produit hermitien : = =

Commençons par ne voir que le membre de droite :

La partie réelle est bien l'image du produit scalaire : produit des modules, par le cosinus de l'angle. Autrement dit, produit contracté d'un vecteur, par la projection intérieure de l'autre vecteur.

La partie imaginaire est ausi l'image d'un produit, couramment appelé "vectoriel", et qui est encore moins vectoriel que le premier n'est scalaire. Ce produit d'un vecteur par la projection extérieure de l'autre, est donc l'aire algébrique de la surface du parallélogramme construit sur les deux vecteurs, orientée en rotation.

En électrotechnique, ce produit est couramment utilisé (sans, bien sûr, être nommé hermitien) : le produit de la tension par le courant, en alternatif, a pour partie réelle la puissance moyenne, ou puissance active, en watts. La partie imaginaire est la puissance réactive, en voltampères réactifs.

Il est temps de regarder aussi le membre de gauche. Très pertinent pour décrire un phénomène avec période et phase, là où les complexes sont compétents. Mais il n'a absolument rien à voir avec toute forme de produit tensoriel, symétrisé ou non, intérieur ou extérieur, de vecteurs. Il n'a absolument rien d'intrinsèque à des vecteurs. Pourquoi nos aînés ont-ils oublié de voir une telle évidence ?

5 .     Hamilton a voulu faire mieux : dans l'espace tridimensionnel.

5 . 1 .  Quand Hamilton s'emmèle (1805-1865).

Faire quelque chose d'isomorphe à l'addition des vecteurs de l'espace, était très simple. Il voulait obtenir l'outil algébrique quotient de deux vecteurs. Tout le drame est que fasciné par l'interprétation confusioniste des complexes, il a voulu prolonger ce confusionisme dans l'espace de dimension 3, agrandir de même la multiplication et la division, et obtenir à nouveau un corps[10]. Il a donc agrandi la confusion entre nombres (complexifiés), et grandeurs physiques. Il a ainsi inventé en 1843, une très belle algèbre, de nombres hypercomplexes, qu'il a appelé les quaternions. Quater__ parce qu'à la recherche du groupe des rotations de E₃ (espace affine à R³), il s'est retrouvé devant un corps de dimension quatre.

A sa mort, Christophe Colomb croyait toujours avoir découvert la route des Indes. A sa mort, Hamilton prenait toujours que ses quaternions pour ce qu'ils ne sont pas : un outil de calcul des transformation de l'espace E₃. Il a fallu attendre en gros E. Cartan (1869-1951) et ses spineurs, et R. Penrose et ses twistors, pour que des mathématiciens prennent conscience (avant tout le monde) de ce que c'est que la complexification d'un espace, et que ce n'est pas exactement la même chose que d'en augmenter le nombre de dimensions.

Dimension 4, donc quatre "vecteurs" de base, et non trois :

(On remarque qu'adieu espace vectoriel de dimension 4 : cette table de multiplication définit un groupe fini à 2 générateurs : i et j, et pas plus, pas 3 ni 4. Car k = ij).

Tout quaternion non nul a un inverse :    x . = 1, où est le conjugué de x.

Les produits croisés sont anticommutatifs : ij = -ji = k.      jk = -kj = i.      ki = -ik = j.

En tant qu'algèbre, c'est à dire espace pré-vectoriel de nombres, muni d'une seconde opération associative et distributive, notée multiplicativement, ceci reste irréprochable (et très fécond). Tout le drame vient de ce que Hamilton et les mathématiciens britanniques, ne savaient pas distinguer un nombre d'un grandeur, ni une longueur d'une surface ou d'un angle, ni un vecteur d'une suite de nombres sans règle ni syntaxe. Ils n'ont pas suspecté combien est malsain le fait qu'une algèbre de nombres se permette de nous dicter subrepticement quelle serait donc la structure de l'espace géométrique de la physique... Les tout premiers soupçons britanniques n'arriveront qu'avec Clifford (1845-1879). Et seul Clerk Maxwell (1831-1879) pensera à la syntaxe des unités physiques, mais sans obtenir de résultats.

Ces produits de quaternions unitaires sont interprétables géométriquement selon ce double sens :

Opérer une rotation I sur une rotation J, donne une rotation K;

Opérer une rotation I sur le vecteur j, donne le vecteur k,

et une rotation J sur le vecteur i, donne le vecteur -k.

Mais il n'a jamais été géométriquement justifié, que multiplier le vecteur i par le vecteur j donne l'objet mal identifié k. Et dans quelle unité ? En mètres ? en mètres carrés ? en radians ?

Et sur la diagonale, les choses prennent aussi une tournure bizarre :

Opérer une rotation I sur une rotation I, donne une rotation -1, ou demi tour; parfait.

Multiplier le vecteur i par le vecteur i donne -1. Bizarre pour un vecteur, de générer l'opposé du produit scalaire. Mais cohérent avec les complexes, que multiplier i par , à la fois conjugué et inverse, donne 1.

Mais pourquoi opérer une rotation I sur le vecteur i, donnerait l'objet mal identifié –1 ? En 1873[11], W. K. Clifford avait déjà souligné que le produit d'un vecteur par un quaternion non perpendiculaire, n'a aucun sens du tout. Signification impossible. Unité physique impossible aussi, évidemment.

Les symétries sont aussi alarmantes : les rotations et les vecteurs ont des comportements opposés.

C'est Hamilton qui a inventé le "vecteur" (quaternion imaginaire pur). Il lui a servi à dériver une force d'un potentiel. Stokes (1819-1903)[12], et Tait (1831-1901)[13] en ont étendu l'usage à la dérivation d'un champ de vecteurs, produisant ce que Clerk Maxwell a proposé d'appeler convergence (opposé de la divergence) pour la partie scalaire, et (avec une grande défiance) rotation (rotationnel) pour la partie "vectorielle".

On voit qu'en dehors de leur beauté algébrique, les quaternions posent des problèmes d'interprétation insolubles, si on prétend les appliquer naïvement à la physique, comme l'ont fait Hamilton, Tait, et Mac Farlane[14]. Gibbs et Heaviside avaient mille fois raison, quand ils objectaient à Tait, que les quaternions ne conviennent pas du tout à la physique. L'ennui, est qu'eux non plus n'ont pas mis dans le mille, et que presque personne - sauf Einstein, Weyl et Cartan - n'a rien fait après eux. Les quaternions appliqués façon 19e siècle, amalgament tout et n'importe quoi, et leur descendant direct, le produit "vectoriel", ne pouvait faire mieux.

Les mathématiciens ont admiré l'audace de Hamilton, et la beauté du corps des quaternions. Ils ont un peu rechigné : la multiplication n'était plus commutative. Ils ont dû vérifier que c'était inévitable. On a généralement oublié de remarquer, que la multiplication des quaternions, est généralement incompatible avec toute projection sur un sous-espace vectoriel. Ce qui est chose grave, pour un espace vectoriel. Les quaternions, comme tout système de nombres complexes ou hypercomplexes, ne sont que pré-vectoriels.

5 . 2 .  Le produit "vectoriel" : fausse solution à un vrai besoin.

Les physiciens ont rejeté les quaternions de Hamilton, à cause de la dimension quatre. Mais pris par l'urgence, prêts à accepter n'importe quoi, qui leur permette des calculs, ils en ont gardé les confusions entre vecteurs et rotations, entre nombre et grandeur. Ignorant les bivecteurs de Grassmann, et se fiant à la foi quaternionienne de son ami Tait, Clerk Maxwell a tacitement utilisé le produit "vectoriel" extrait des quaternions. Ce produit "vectoriel", et cette confusion, rendirent incompréhensibles un tiers de l'électromagnétisme et de la mécanique, avec d'absurdes lois chirales et de travers. Maxwell était conscient du problème, sans avoir de solution[15], et il est mort à 48 ans. Inconscients, les autres ont ignoré les mises en garde de Maxwell.

Incompatible avec la définition des vecteurs comme classes d'équivalence de bipoints, et même avec les axiomes des espaces vectoriels, par exemple avec la projection sur un sous-espace vectoriel, le "produit vectoriel" a été extrait (par restriction, ou projection) du produit de quaternions imaginaires purs.

La grosse différence, est qu'il n'y a plus d'élément neutre, ni plus aucun inverse. Tandis qu'apparaissent des diviseurs de zéro. Le carré de tout "vecteur" est désormais nul :   i x i = j x j = k x k = 0.

C'est ainsi que l'on perd l'associativité, qui était préservée en quaternions :

(i  x j) x j = -i   (même résultat qu'en quaternions), mais  i x (j x j) = 0.

Cette perte de l'associativité contredit directement l'intention sémantique initiale : Tout ça c'est des vecteurs, ils se valent tous. Et leur ordre m'importe peu, il me suffit de changer le signe du résultat, quand je permute le multiplicateur et le multiplicande. La non-associativité prouve la contradiction interne. Retenons donc que, en syntaxe cohérente, l'ordre des termes ne sera jamais libre : le gyreur strict agit sur le vecteur.

Le produit "vectoriel" implique deux résultats joliment absurdes :

En physiciens, donnons une longueur concrète à nos vecteurs. Si les vecteurs i, j, k sont de longueur 1 mètre, alors k, qui est le produit de i par j, est de longueur 1 m². D'autre part, i et j sont de longueur 100 cm, donc k est de longueur 10 000 cm². D'autre part, j, produit de k par i, est alors de longueur 1 m³. Donc i, produit de j par k, est de longueur 1 m⁵, ou 10¹⁰ cm⁵. Etc... etc... Il n'y a aucune limite à l'absurdité.

D'autre part, rappelons-nous la définition des vecteurs comme classes d'équivalences de bipoints.  Considérons donc ce trièdre, dans un miroir parallèle au plan xOz, k est conservé par la symétrie, mais j est retourné, donc k, produit "vectoriel" de i par j, est retourné en -k. Donc k = -k. On peut recommencer sur les deux autres vecteurs de base, et on peut étendre par combinaison linéaire.

Ce qui démontre que la composante vectorielle, du produit "vectoriel", est identiquement nulle.

Nous avons donc démontré, par deux fois, que le produit "vectoriel" est une opération invalide.

C'est avec cette algèbre contradictoire avec elle-même, que les physiciens du 19e siècle, ont cru résoudre mathématiquement, le problème des gyreurs, dont ils avaient besoin, et dont on a toujours besoin.[16]

Cette construction, ayant tourné le dos à la géométrie et à la physique, garde les défauts des complexes et des quaternions naïfs : impuissants à respecter les unités physiques, et l'exigence de covariance des lois physiques. Tout s'écroule au premier changement de repère non orthonormé. Incohérente avec les unités physique, et les vecteurs de base physiques, et incohérente avec les lois de la dérivation[17], cette construction confond les mètres avec les mètres carrés, et avec les angles, parce qu'elle refuse de distinguer les nombres des grandeurs. Physiquement, elle est désastreuse. Pédagogiquement, elle brave l'expérience, et le bon sens. Elle contredit et bafoue le cahier des charges de la physique. Le "vecteur" de physicien, jamais défini, a dévoré les lois de la dérivation. The tail wags the dog.

Pour simplifier ? Il suffit d'écouter les conversations entre professeurs d'électrotechnique (qui sont la population-prétexte du pour simplifier), pour avoir la preuve que seules de longues années de dressage, leur permettent de ne plus s'embrouiller entre main droite et main gauche, aux trois doigts prétendus indispensables, l'une pour un moteur, l'autre pour un générateur (ou l'inverse ?). Pour simplifier ! Quel gâchis !

Pour représenter simplement les quarts-de-tour, présents dans quelques lois de la physique, les moyens mathématiques corrects existent au complet depuis 1888[18]. Weyl en 1918[19], puis Einstein en 1921[20], ont montré à quel point ils sont pratiques, et pas plus difficiles que le jargon petit-nègre inscrit au programme officiel.

L'algèbre pertinente est l'algèbre tensorielle. Ici, il nous suffit de son sous-ensemble, l'algèbre extérieure, créée par Hermann Grassmann en 1844, qui convient à tous les besoins de la physique élémentaire : elle a exactement la bonne structure, isomorphe à la classe de phénomènes physiques que nous étudions. Au 19e siècle, seul Grassmann flaire le piège de la confusion entre nombre et grandeur, et dénonce ce piège. Encore restait-il à cesser d'oublier de compléter l'algèbre tensorielle abstraite, par l'algèbre des unités physiques.

6 .     Un gyreur opère la partie infinitésimale d'une rotation infinitésimale.

Pour les rotations, on a besoin de l'opérateur de rotation infinitésimale, qui se compose de l'identité, et d'un  gyreur strict, opérateur de différentiation antisymétrique, qui agit généralement sur des vecteurs.

Le gyreur physique comprend une dimension physique. Il sert pour tout ce qui accompagne les rotations, et pour tout ce qui se déduit directement des rotations infinitésimales, en physique : vitesse angulaire, accélération angulaire, moment angulaire, couple, champ magnétique B, dipôle magnétostatique.

Opérateur de différentiation antisymétrique, un gyreur n'a ni centre de rotation, ni axe de rotation, aucun sous-espace invariant (qui seraient indispensables pour décrire des rotations de solides[21]).

Un gyreur ne contient que les trois informations suivantes :

  sa direction de plan stable (sur lequel s'opère la projection),

  sa grandeur algébrique, décomposable en un quart de tour à droite ou à gauche, et un multiplicateur,

  une unité physique, contenant, sauf exception, la longueur à la puissance 2, ou 0 (ou -2 ?).

Sur E₃, un gyreur a pour noyau (préimage de zéro) le sous-espace supplémentaire à son plan stable.

6. 1.    Gyreur strict : opérateur associé à une rotation infinitésimale stricte,

caractérisé par l'absence apparente de la dimension longueur. Absence apparente seulement, car il s'agit d'une longueur divisée par une longueur perpendiculaire. Cela semble ne faire rien, mais ce rien n'est vrai qu'en repère orthonormé, et seulement à condition d'oublier le radian dans le monôme dimensionnel.

Sténo graphique du gyreur strict en relation avec deux vecteurs.

6 . 2 .  Gyreur étendu (ou bivecteur) : opérateur d'inertie en rotation.

Est homogène à un gyreur strict, multiplié par le carré d'une longueur (une surface).

Sténo graphique du gyreur étendu, en relation avec deux vecteurs.

Le gyreur étendu est produit extérieur de deux vecteurs vrais V1 et V2. On l'a représenté comme une surface grisée, car si les deux vecteurs étaient bien homogènes à des longueurs (multipliés éventuellement par d'autres grandeurs physiques), lui est bien homogène à une surface (multipliée éventuellement par d'autres grandeurs physiques).

Ceci représente bien une loi comme celle du moment angulaire, produit extérieur du rayon vecteur par l'impulsion. Ou le moment d'une force, produit extérieur de la force par le bras de levier.

6 . 3 .  Densité volumique de gyreur étendu.

Exemple : le champ de dimension  [L^-1.T^-1. Q]. Vérifions que ce gyreur est bien une densité volumique de quelque chose à préciser :                     L³. :                         [L² . T^-1 . Q].

C'est bien la dimension attendue d'un gyreur : vitesse aréolaire d'une charge électrique autour d'un axe.

Il existe d'autres combinaisons moins fréquentes : cogyreur, en [L^-2], capacité de cogyreur, en [L¹]. En électromagnétisme, ceci peut encore se compliquer, par l'intervention de la célérité de la lumière c.

6 . 4 .  Tables de multiplication EXTERNES :

où i, j, k sont les vecteurs unitaires orthonormaux, K, I, J, sont les rotations unitaires (autrement dit, quarts de tour) dans les trois plans de base.

où i, j, k sont les vecteurs unitaires orthonormaux, K, I, J, sont les rotations unitaires, quarts de tour dans les trois plans de base, et u l'unité de longueur.

6 . 5 .  Associativité : rang trois.

Produit extérieur d'un gyreur et d'un vecteur = tenseur antisymétrique de rang trois. Résultat nul en dimension deux. Une seule composante libre en dimension trois, sur une base orthonormale :

permutations paires : i^j^k = j^k^i = k^i^j =  u³.V        (volume orienté dans l'ordre des vecteurs de base).

Impaires :                 k^j^i = i^k^j = j^i^k = -u³.V        (volume orienté dans l'ordre inverse des vecteurs de base).

Avec V : unité de base, sans dimension, de tenseur antisymétrique de rang trois (ici sur l'espace R³).

Le produit extérieur de vecteurs non indépendants est toujours nul. Donc au delà du rang trois sur un espace de dimension 3, ni au delà du rang 4 sur un espace de dimension 4, tout produit extérieur est nul.

6 . 6 .  Une grandeur gyratorielle, c'est un gyreur, éventuellement multiplié par d'autres unités physiques non géométriques.

Nous séparons les dimensions physiques en deux parties :

Une partie géométrique, contenant la longueur, donc la dimension du gyreur, usuellement [L²] ou [L⁰],

et le restant, qui peut contenir une unité de masse, une ou plusieurs fois l'unité de temps, l'unité de charge électrique, éventuellement le Kelvin (rarement un volume ou son inverse, ou c, célérité de la lumière).

Nous faisons donc une fois pour toutes, les mathématiques de la partie géométrique du gyreur.

7 .     Trois traditions.

7 . 1 .  Tradition tout-vecteur : Hamilton (1843), Clerk Maxwell (1873), Heaviside (1893)

Cette façon cumule les deux erreurs majeures :

    C'est un bâton, et ça tient sur une droite.

    Ça ne tourne plus, ça court le long de la droite.

(Il est vrai que sur un arbre lisse, une poulie folle peut coulisser ou tourner, ou les deux, et qu'à l'époque, on distinguait mal entre la physique, et la cinématique du solide indéformable.)

Descendance oubliée : les dyadics de Josiah Willard Gibbs (1839-1903).

J. W. Gibbs a bien eu l'idée de désigner les tenseurs de rang 2 - ou leurs matrices, on ne savait pas très bien - sous le nom de "dyadics", tout en conservant intégralement les masques traditionnels de "vecteurs" et de "produit vectoriel" partout où la tradition de l'époque en mettait (environ 1881-1884, diffusion restreinte)[23]. On peut encore rencontrer des dyadics dans la littérature américaine.

“Frenchman, Germans, and Italians, urging their respective substitutes for quaternions, added to the din. By the second decade of the twentieth century there was a babel of conflicting vector algebras, each fluently spoken only by its inventor and a few chosen disciples.”[24]

Autrement dit, c’était une guerre de l’Empire Britannique contre les géomètres, algébristes et physiciens continentaux.

7 . 2 .  Tradition universitaire minoritaire (depuis Pierre Curie ? 1894 ?).

    Au moins, ça tourne, dans le même sens que le phénomène physique.

    Une seule erreur : c'est un bâton, dit "vecteur axial".

Il existait un élément de cohérence, limitée exclusivement à un espace de dimension 3 : la fibre ainsi exhibée, munie du même sens de rotation que le plan stable, en est sa duale. On s'empêchait de traiter simplement les problèmes de dimension 2. On s'empêchait de passer facilement aux dimensions 4 et plus.

Et on appela ce bâton tournant "vecteur axial", sans se préoccuper de la contradiction : vecteur ou pas vecteur ? Et faute d'avoir pensé à achever le travail d'algébriste, on conserva le produit "vectoriel", qu'on venait de dénoncer comme trompeur. Et si ce que l'on dessinait avait bien les bonnes symétries, ce que l'on calculait en avait toujours de fausses, qu'il fallait corriger après coup, à l'instinct, car on le calculait exactement comme pour un vecteur. A tort.

Ecrire les équations de Maxwell dans ce système semi-cohérent, était un pont aux ânes, que les auteurs ne franchissaient pas tous indemnes. Si Denis-Papin et Kaufmann[25] déjouaient le piège laissé tendu par la notation de Gibbs, d'autres y tombaient[26].

Moins scrupuleux, d'autres, pour simplifier, enseignaient par défaut la version forte de la confusion (tout-vecteur), mais en cas de public plus perspicace, plus interrogatif, se dédouanaient par la version faible : nuance axiale. Puis on s'embrouillait, et on sautait de cheval au milieu du gué, en invoquant la profondeur des algèbres de Lie.

7 . 3 .  Manière correcte : H. Grassmann 1844, G. Peano 1888, H. Weyl 1918, A. Einstein 1921, E. Cartan, J. Barbotte 1948.

    Ça tourne,

    C'est dans un plan.

8 .     Symétries comparées.

Le vecteur, même nuancé par l'adjectif "axial" - d'ailleurs à contresens : aucun axe n'existe - conduisait invariablement à une erreur de symétrie, dictée par l'outil mathématique inadéquat. Au contraire du gyreur, qui dans chaque cas a exactement le comportement exigé par sa signification.

L'enseignement du vecteur-à-la-place-de-la-rotation, a joué un autre tour pendable aux physiciens qui y ont cru : on leur a interdit les symétries, puisque le produit "vectoriel" n'y résiste pas. Cela les a dépouillés de la conscience de l'utilité élémentaire des symétries, et ça les a embrouillés d'une chiralité mystique qui n'a rien à voir avec les lois physiques, n'étant produite que par un choix erroné d'outil mathématique, en 1843.

La symétrie, ça sert d'abord à ramener de nouveaux problèmes, à des problèmes déjà connus, et résolus. On gagne donc du temps.

Ça sert aussi à appliquer le principe de Pierre Curie : L'effet est au moins aussi symétrique que la cause. Réciproquement, c'est la dissymétrie qui crée le phénomène. Ce principe est trop puissant pour qu'on puisse se permettre de s'en passer. Il permet notamment de prédire des nullités, ou des égalités, de certaines composantes. Par exemple la présence ou l'absence de piézoélectricité.

9 .   Coordonnées d'un gyreur, en repère orthonormé.

9 . 1 .  Cas du gyreur strict, quotient.

Nous menons le calcul sur l'exemple de la rotation uniforme, avec la relation : = où relie deux vecteurs orthogonaux.

9 . 2.   Calcul rigoureux.

Feignons d'ignorer tout du calcul matriciel, des représentations matricielles, mais en sachant tout de même la trigonométrie.

Mimant l'ignorance totale, nous allons même ignorer qu'il est plus pratique de les ranger en tableau carré. Rangeons donc provisoirement en ligne les quatre influences-d'une-coordonnée-de-R-sur-une-coordonnée-de-V (les signes affectant des valeurs absolues, dépendent évidemment du signe de la rotation, par rapport à l'orientation des axes de coordonnées) :

Premier mouvement de panique : Ces coefficients sont trop compliqués !

Mais remarquons que ces coefficients sont deux à deux redondants, et que si nous les appliquons simultanément, nous obtiendrons à chaque instant le double de la vitesse .

Vx =  ½ V/R (+ Rx tg θ - Ry )

Vy =  ½ V/R (+ Rx + Ry cotg θ )

Nous avons intérêt à scinder ces coefficients en deux groupes, dont chacun est suffisant :

Or, seul le groupe de la première ligne a la propriété d'être invariant envers θ. Lui seul donc est digne de représenter l'être physique "vitesse angulaire de rotation", qui lui, est un invariant quel que soit θ. Le second groupe conviendrait pour décrire une oscillation harmonique droite. Ici ce n'est qu'une fausse solution, proposée par notre mathématisation : un groupe non faux, mais sans intérêt, et affligé de discontinuités rédhibitoires pour = π/2 + kπ.

Une autre façon équivalente, d'apparence plus rigoureuse, est de faire la moyenne des coefficients trouvés, en faisant varier θ de 0 à 2π. Les termes en tg θ et cotg θ s'annulent en moyenne. Ce qu'il fallait démontrer.

Il ne reste plus au lecteur, qu'à se convaincre de l'intérêt de disposer ces quatre coefficients retenus, sous la forme d'un tableau carré, au lieu de les entasser en ligne.

9 . 3 .  Calcul simplifié.

R¹₁ = R

R¹₂ = 0 (1ère coordonnée du 2e vecteur)

R²₁ = 0 (2ème coordonnée du 1er vecteur)

R²₂ = R

V¹₁ =  0

V¹₂ = -V          (1ère coordonnée du 2e vecteur)

V²₁ =  V           (2ème coordonnée du 1er vecteur)

V²₂ =  0

On résout le système suivant, où les coordonnées de sont les inconnues :

                    (produit matriciel, ordinaire)

_{D'où la solution: (coordonnées de ) =}

            ω¹₁ = 0

            ω¹₂ = -1            (1ère coordonnée du 2e vecteur)

            ω²₁ = 1 (2ème coordonnée du 1er vecteur)

            ω²₂ = 0

On remarque qu'en repère orthonormal, les coordonnées mixtes se comportent comme des coordonnées homogènes, et sont sagement antisymétriques. Il ne reste bien qu'une seule coordonnée stricte non nulle. En repère non orthonormal, il faut revenir à la discipline de base, et n'antisymétriser que des coordonnées homogènes : entièrement covariantes, ou entièrement contravariantes. Nous y reviendrons.

Mais attention à un oubli qui pourrait nous coûter cher ultérieurement : le gyreur ne caractérise la rotation que du seul point de vue différentiel. A lui seul, il perd une constante d'intégration capitale : le sous-espace invariant. C'est à dire le centre de rotation dans le plan, ou l'axe de rotation dans l'espace R³. Souvenons-nous en quand nous étudierons le moment angulaire.

Nous suggérons de regarder ce tableau ω ⁱ_j, comme un tableau de dérivées partielles des coordonnées de par rapport aux coordonnées de . Comme tout tableau, il est à double entrée : selon l'origine, et selon l'image : ωⁱ_j

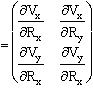
Et ainsi qu'on l'a vu, on ne retient que les termes dont la moyenne est non nulle, quand le nombre de rotations tend vers l'infini.

Dans tous les cas, on peut traiter le problème sous forme plane : il suffit de déterminer son plan stable, et projeter ce qu'il faut, vers le plan stable.

9 . 4 .  Cas du gyreur étendu, produit extérieur.

Faire le produit tensoriel[27], et retrancher le transposé : = = ou en coordonnées : U_ij = V_iW_j -V_jV_i .

Déroulons à deux dimensions :          U_ij

Déroulons à trois dimensions :           U_ij

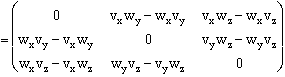
On a donné l'exemple entièrement en coordonnées covariantes. La définition est similaire, sans surprises, en coordonnées contravariantes. Elle ne serait valide en coordonnées mixtes, qu'à condition que le repère soit orthonormé.

9 . 5 .  Exercice. Utiliser le produit extérieur en quotient :

Montrer que = implique ₌ (La réciproque est fausse, sauf si ).

Cela montre que comme en algèbre de quaternions, on sait calculer des "inverses", plus exactement des duaux, mais désormais, on respecte la covariance des lois physiques :

A tout vecteur non nul, on peut associer le covecteur dual ("inverse sur la même droite") : = .

A tout gyreur, on peut associer le cogyreur dual ("inverse dans le plan stable") : =

10 .   Syntaxe algébrique et géométrique.

La règle de grammaire dimensionnelle des vecteurs et des gyreurs, oblige à un parfait isomorphisme avec la bonne règle physique. Une grammaire stricte est un garde-fou, indispensable aux physiciens. Pas seulement aux informaticiens (Don't shoot yourself in the foot any more !)...

Comment corriger les anciens produits "vectoriels" de vos manuels.

Vous devez corriger vos manuels, loi par loi, des bévues qui, pour simplifier, les obscurcissent. Concernant les anciens produits "vectoriels", on ne rencontre en pratique que quatre cas.

Pour trois d'entre eux, la règle de grammaire, est de repérer dans une ancienne formule, qui au juste est un gyreur. On trouve toujours un seul gyreur, en formule avec deux vecteurs[28]. Il suffit souvent, mais pas toujours, de regarder son monôme dimensionnel, pour démasquer une grandeur physique mystérieuse.

Nous verrons plus loin le quatrième cas, avec le théorème d'Ampère.

Pour la clarté, nous écrivons les produits "vectoriels" à l'anglo-saxonne (à la façon du 19e siècle), avec une croix oblique ()x, au lieu du V renversé (^), que nous réservons au seul produit extérieur.

10 . 1 .            Cas 1 : Produit extérieur de vecteurs = gyreur étendu.

Presque la même écriture, en apparence. Pas la même signification. On garde la liberté d'utiliser l'anticommutativité, pour éliminer le signe + ou - qui nous semble disgracieux.

10 . 2 .            Cas 2 : Un gyreur multiplie un vecteur = un vecteur perpendiculaire.

Pas de liberté pour le choix du signe : le gyreur est à gauche, le vecteur à droite. Ce serait l'inverse pour un covecteur. L'anticommutativité semble bien absurde : on n'anticommute que des êtres de même nature.

Une formule :  , avec gyreur, ce qui implique , se traduit par :

10 . 3 .            Cas 3 : Quotient extérieur de vecteurs = gyreur strict.

Une formule :  , dans le cas où est le gyreur, se traduit par :  ₌

11.      Position dans le livret de famille.

Les gyreurs stricts, et les gyreurs étendus (bivecteurs), ont la même symétrie. Ce sont tous des tenseurs antisymétriques de rang 2. Les vecteurs et les covecteurs, sont les tenseurs de rang 1. Les scalaires, tels que la température, sont les tenseurs de rang 0 (zéro). L'enseignement de la physique élémentaire n'a pas besoin d'autres tenseurs de rang 2, autres qu'antisymétriques, excepté pour le moment d'inertie d'un solide.

11 . 1 .            Difficulté réelle : moment angulaire et moment d'inertie.

Moment angulaire pour un point matériel : = =

= pour un solide.

et sont des gyreurs, mais est un tenseur symétrique, représentant l'inertie autour du centre d'inertie. M est la masse totale du solide, le vecteur distance de l'axe de rotation au centre d'inertie du solide (vecteur perpendiculaire à cet axe). sont aussi de nature tensorielle Si par malchance, est non nul, ou si aucun des axes principaux de n'est contenu dans le plan principal du gyreur votre solide vibre ! Autrement dit le moment angulaire ne garde pas une orientation constante au cours de la rotation, mais précesse autour de l'axe de rotation. Leonhard Euler donna la première expression des axes principaux d'inertie, et des moments autour des axes principaux, vers 1760.

Sténo graphique ? Dessiner le plan de et l'ellipsoïde d'inertie. On n'échappe pas à la difficulté principale, liée au dessin de l'ellipsoïde. Il n'existe pas ici de sténo graphique plane. On retrouve le même problème pour un solide au magnétisme anisotrope, où et ne sont pas nécessairement coplanaires.

11 . 2 .            Difficulté peu utile : le théorème d'Ampère

Le théorème d'Ampère énonce l'égalité de deux tenseurs antisymétriques de rang trois dans un espace R³. Il n'ont donc qu'une seule composante stricte ("pseudo-scalaire" : faux scalaire).

Il n'existe pas ici de sténo graphique plane. De part et d'autre du signe = (égale), le problème est vraiment tridimensionnel, et des deux côtés, l'orientation de la surface, et de son bord sont arbitraires.

11 . 3 .            Le rotationnel, ou dérivée extérieure d'un champ tensoriel (d'ordre non nul).

Dérivée extérieure signifie : dérivée covariante antisymétrisée.

11 . 3 . 1 .                   Cas historique : rotationnel d'un champ vectoriel : = =

Dans ce cas, il n'y a qu'une seule permutation possible sur la base, donc B_ij = A _i,j - A _j,i.

L'antisymétrie ne garde son caractère invariant qu'en coordonnées homogènes, toutes covariantes dans le cas général[29] (toutes contravariantes aussi, en espace métrique; les coordonnées mixtes ne deviennent tolérables que si on se limite aux repères orthonormés, limitation qui a produit de dangereuses habitudes confusionistes).

Définition initiale pratique : prenez un solide indéformable, en rotation. Faites l'opération rotationnel sur son champ des vitesses instantanées : en tout point, vous trouvez une grandeur constante, qui est le double de la vitesse de rotation instantanée du solide, autour de son centre de rotation instantanée.

₌ de coordonnées  2ωⁱ_j

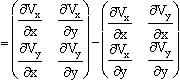
Ceci justifie que Stokes et Tait aient inventé l'opération rotationnel, lui donnant à peu près ce nom.

Le rotationnel est indispensable en mécanique des fluides. Le demi-rotationnel est aussi appelé le tourbillon. La dérivée covariante complète, est donc la somme du tenseur tourbillon, antisymétrique, et du tenseur de déformation, symétrique. Le rotationnel permet de décrire avec naturel les "ronds de fumée", les tourbillons, les portances sur les profils d'ailes ou de voiles, ou sur les rotors de Flettner. Au temps où l'on assimilait le rotationnel à un vecteur, ce naturel disparaissait, et les figures s'encombraient très bizarrement.

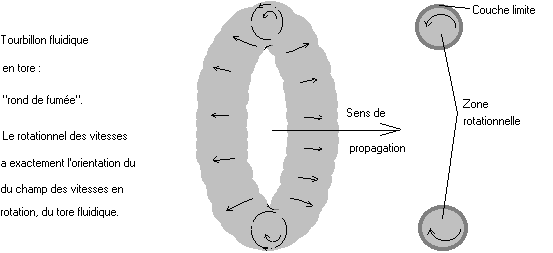
Cruelle, la comparaison avec l'original : figure 40 - 15, du cours de Feynman, Leighton et Sands, regardez leurs lignes de tourbillon. Quel gâchis, ce respect des traditions absurdes !

11 . 3 . 2 .                   Cas général de la dérivation extérieure, en dimension n.

Soit une p-forme différentielle (1< p< n) : ω = , sa dérivée extérieure dω s'écrit :

dω = = .

Le lemme de Poincaré[30] établit que : d(d ω) = 0. Donc le rotationnel d'un rotationnel, est identiquement nul.

11 . 4 .            Les équations de Maxwell, débarbouillées par Einstein en 1921.

La confusion "tout-est-vecteur", avait fait permuter divergence et rotationnel sur les gyreurs déguisés en vecteurs. Les deux divergences reprennent leur vraie place, liées à la conservation de la charge électrique.

=  µ₀            ( =  )    [M.L^-1.T^-1.Q^-1]            (Egalité vectorielle).

div =                                                     [M.T^-2.Q^-1]                  (Egalité scalaire).

= 0                                 [M.L^-1.T^-1.Q^-1]            (Rotationnel du rotationnel nul)

_{= 0}                                              [M.T^-2.Q^-1]                  (Somme gyratorielle nulle).

Enfin propres, enfin rationnelles envers les quatre dimensions d'espace et de temps, ces équations sont clairement les projections des deux équations quadridimensionnelles. Elles n'incitent plus à inventer de mythiques monopôles magnétiques, pour justifier la faute mathématique originelle.

11 . 5. Topologie des champs gyratoriels.

On sait que les hérissons et les bogues de chataignes existent : il est possible d'avoir un champ vectoriel sortant de manière uniforme d'un sphère S₂ de l'espace E₃. C'est la situation d'enseignement du théorème du flux de Gauss.

On sait aussi qu'il est impossible de peigner entièrement un hérisson: sur la sphère S₂ de l'espace E₃, il restera toujours au moins un point singulier non peignable (le plus souvent deux points singuliers), alors qu'un plan, un cylindre infini, ou un tore, sont peignables.

A première vue, il semble possible de coucher sur toute cette sphère S₂ un champ gyratoriel uniforme non nul, comme sur un plan, sur un cylindre, ou un tore, comme si on y couchait un scalaire quelconque. A peu près comme si chaque piquant du hérisson était vrillé, tous dans le même sens. Mais rappelons nous qu'il n'existe aucune situation où le champ gyratoriel ait été introduit librement, sans contraintes. Il a toujours exprimé la partie infinitisémale d'une isométrie infinitésimale. C'est donc cette isométrie qui impose la topologie admissible dans un champ gyratoriel.

En particulier, pour que le gyreur d'une rotation soit exactement couché sur la surface, il faut que son plan soit perpendiculaire à la droite invariante. Pour qu'un gyreur soit partout couché, il faut que toutes les normales à la sphère, soient des directions de droite invariantes, donc que la transformation soit identique, et le gyreur nul.

En d'autres termes encore, le gyreur ne s'obtient que par produit extérieur, ou par quotient extérieur de deux champs de vecteurs, qui ont tous au moins un point non peignable, selon le théorème cité plus haut.

Encore en d'autres termes : le champ B n'existe que bordé par la circulation d'un potentiel A. La sphère n'a pas de bords, même à l'infini, donc la circulation donnant un B uniforme, est nulle, donnant un B nul.

Il est donc impossible de coucher sur toute cette sphère S₂ un champ gyratoriel uniforme non nul. Alors que c'est trivial sur un plan, sur un cylindre, ou un tore. Il en résulte que le mythique monopôle magnétique, ou charge magnétique, est topologiquement impossible, au moins dans l'espace géométrique ordinaire, où on le cherche généralement.

Et pourtant, on enseigne partout qu'il est correct de substituer un champ vectoriel au champ gyratoriel: leurs propriétés topologiques sont radicalement incompatibles.

Dans l'armée, on envoie les bizuts chercher la clé du champ de tir ; dans la marine à voiles, on les envoie chercher l'échelle de Beaufort ; en montagne, on les envoie à la chasse au dahut. En physique des particules, on les envoie chercher des monopôles magnétiques, à titre de "rite d'initiation"¹…

12 .   Prochaines actions, et moralité.

Nous examinerons plus tard les carences méthodologiques, et les mécanismes sociaux, qui ont pu verrouiller une aussi grosse bévue pendant 150 ans et plus, et qui ont pu en faire le bizutage d'entrée dans la profession de physicien. Toujours, les moyens mathématiques acceptés, furent nettement en retard sur les besoins.

Les physiciens n'ont pas lu les outils établis par Hermann Grassmann[31] en 1844 et 1862. Côté mathématiciens, W.R. Hamilton a calembourdé leur auteur, et s'est contenté de vérifier que Grassmann n'antériorisait pas ses quaternions, sans rien voir d'autre. Clifford n'a découvert l'Ausdehnungslehre qu'un an avant sa mort, et celle de Maxwell[32]; et sa lecture n'est pas celle d'un physicien. Le cadre ensembliste indispensable n'a été apporté qu'en 1888 par G. Peano (1838-1932)[33]. Les moyens tensoriels publiés en 1888, n'ont été diffusés avec d'amples exemples d'applications qu'en 1901, à la demande de Felix Klein (1849-1925), par Ricci-Curbastro (1853-1925) et T. Levi-Civita (1873-1941)[34], dans l'indifférence générale des physiciens[35]. Qui les connaîtrait, si entre 1912 et 1914, Marcel Grossmann (1878-1936) n'avait pris la peine de les enseigner à un certain Albert Einstein (qui en fit quelque usage retentissant) ? Du reste, il semble qu'on ait systématiquement sous-estimé le rôle clarificateur des mathématiciens italiens des 19e et 20e siècles : par exemple, G. Bellavitis (1803-1880) a dès 1832, donné une définition claire de l'équipollence des vecteurs[36].

Même durant les années 60-70, de nombreux exposés de la Relativité restreinte, restaient incapables de distinguer si l'espace-temps de Minkowski (1864-1909), était un vrai espace de dimension 4 réelle, pseudo-euclidien, ou un espace de dimension 3 réelle, tiers-complexifié par une dimension temps imaginaire. Le concept de complexifié d'un espace n'était absolument pas dégagé. Or seul un espace de Minkowski de dimension 4 réelle, est complexifiable à la dimension 8, pour y loger les antécédents des spineurs. Mais ces professeurs-là n'y avaient nullement pensé, étant trop peu cultivés en électrodynamique quantique.

Aujourd'hui, il s'agit de restituer à la physique les outils mathématiques transparents qu'elle n'aurait pas dû rater pendant 150 ans. Le prochain article donnera les "travaux dirigés", permettant à chacun d'être au clair dans sa pratique calculatoire. Un autre rassemblera les expériences fondamentales à présenter aux élèves, au lieu de recommencer à les abuser avec les spectres de limailles de Faraday.

Au 16e siècle, Ambroise Paré écrivait : “Il ne faut pas couper les couillons aux garçons !” En ce temps-là, des châtreurs faisaient croire aux mères, qu'en châtrant leurs fils, ils les préserveraient à vie de toutes sortes de maladies mortelles... En notre temps, j'écris : “il ne faut plus enseigner le produit vectoriel.” Le contribuable nous confie ses enfants pour en faire d'honnêtes physiciens, pas pour les assotter à coups de contes de fées et de sornettes.

Maria Montessori a osé expérimenter, ce qui l'a conduit à inventer l'école maternelle moderne. Osez vous aussi la démarche qualité : donnez à vos élèves les moyens de pratiquer les deux présentations, pratiquez notamment les moyens graphiques plans. Et le tri se fera tout seul...

Auteur : Jacques Lavau