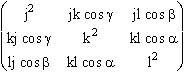Repérer un point par ses coordonnées sur un repère. Projeter un point sur les axes du repère. Les translations dans le plan ou l'espace. Le parallélogramme. L'angle d'une droite et d'un plan. Les sinus et cosinus.

1 . Rappels : un vecteur, c'est d'abord pour les translations,

et c'est pour tout ce qui se déduit directement des translations, en physique : vitesse, accélération, quantité de mouvement, force, champ électrique, dipôle électrostatique, vitesse de diffusion ionique.

1 . 1 . Définition : classe d'équipollence des bipoints.

Le cahier des charges est de caractériser l'opérateur de translation. La définition formelle répondant à ces réquisitions, définit le vecteur comme classe d'équivalence de bipoints, par la relation d'équipollence. Cette définition est la plus petite qui couvre toutes les propriétés géométriques réellement utilisées par la physique.

Un bipoint : c'est un couple de points, respectivement le premier, ou point de départ, et le second, ou point d'arrivée. On le note (A,B).

On peut définir une addition : si le départ du second, est exactement l'arrivée du premier,

(A,C) = (A,B) + (B,C),

Exemple : se rendre de Paris à Lyon, puis de Lyon à Marseille, revient à se rendre de Paris à Marseille. Puisqu'on ne s'intéresse qu'au point de départ, et au point d'arrivée.

C'est la relation de Chasles.

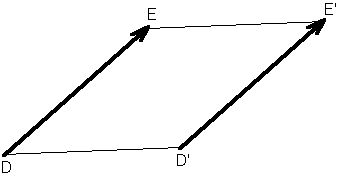
Ajoutons l'hypothèse que dans notre espace E, le postulat d'Euclide soit vérifié : la parallèle d'une droite passant par un point, existe, et est unique. Dans ce cas, les parallélogrammes existent.

Définition : Les bipoints (D,E) et (D',E') sont dits équipollents si le quadrilatère DEE'D' est un parallélogramme.

De l'addition des bipoints, on déduit l'addition des vecteurs : pour tous points A, B, et C, = + .

Dans un espace euclidien, et grâce aux parallélogrammes, on peut transporter les extrémités d'un bipoint, les éléments caractérisant une translation. Plus tard, pour parler d'orthogonalité, nous aurons besoin de choisir une norme euclidienne parmi toutes celles possibles.

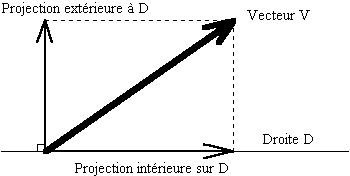
2 . Rappels : quatre projections pour la physique.

Puisque nous savons faire la somme et la différence de deux vecteurs, nous savons projeter sur un sous-espace, parallèlement à un sous-espace complémentaire. Le choix le plus simple, physiquement le plus fécond, est de prendre la direction perpendiculaire.

Prenons désormais le choix de projection orthogonale à D. La décomposition de est alors unique :

= + .

On désigne le restant de l'opération projection, , la projection extérieure de sur D.

est la projection intérieure.

D'où la définition sommaire du produit intérieur : produit d'un vecteur, par la projection intérieure de l'autre.

Et la définition sommaire du produit extérieur : produit d'un vecteur, par la projection extérieure de l'autre.

Ceci est indispensable à la physique. On l'étend facilement aux tenseurs d'ordre supérieur.

Avec un plan P et un vecteur, on définit de la même façon, la projection intérieure sur ce plan : , et la projection extérieure au plan : , qui est orthogonale à tout vecteur de P.

En considérant les covecteurs inverses (sur un espace métrique), on définit de même les projections anti-intérieure, et anti-extérieure.

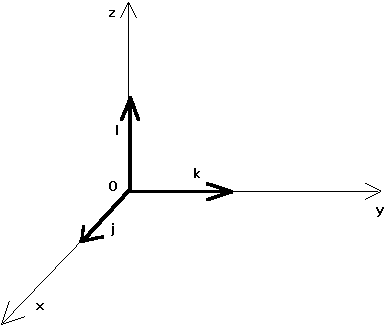
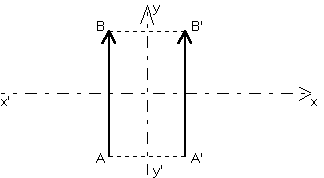
1. Coordonnées d'un vecteur.

3 . 1 . Repère

On ne peut décrire une position d'un point que par rapport à un repère.

Un repère cartésien (le plus utilisé) se compose d'une origine, d'exactement autant de directions d'axes qu'il en faut (par exemple 2 en géométrie plane, 3 en géométrie dans l'espace), et du même nombre de vecteurs unitaires sur chaque axe.

Unitaire, signifiant qu'il est de longueur unité.

On se simplifie beaucoup la vie, quand on peut choisir des axes orthogonaux entre eux, et ayant la même unité de longueur sur chaque axe. On appelle un tel repère, un repère orthonormé.

Dans la géométrie courante, on peut faire ce choix d'orthonormalité, et on le fait systématiquement. Si notre métier s'occupait de cristaux (cristaux métalliques, comme dans tous les métaux et alliages, ou cristaux minéraux, comme dans le mica, ou le quartz), parfois nous pourrions prendre un repère orthonormé dans le cristal (cas du cuivre, de l'aluminium), et d'autres fois, ce choix serait désastreux (cas du mica, du quartz, du magnésium, etc...). Les cristallographes (ceux dont le métier s'occupe de cristaux, par exemple pour étudier des piézoélectriques, des ferromagnétiques, des supraconducteurs) préfèrent de loin prendre un repère qui épouse les directions et unités du cristal. Il leur a donc fallu apprendre un peu plus de géométrie, et d'algèbre linéaire, pour rester capables de calculer juste, à partir de repères non orthogonaux, et dont les unités selon les axes ne sont pas nécessairement égales. Même problème en mécanique des élastomères : un repère lié à la matière au repos, n'est plus orthonormé, ni même euclidien, quand la matière est déformée.

Avoir choisi un repère, permet de privilégier une certaine sorte de projection : la projection sur les axes de coordonnées. Il est possible de projeter tout vecteur sur les axes du repère. Si on nomme , , , les axes de ce repère, on pourrait nommer , , , les trois projections de sur ces trois axes. La règle du jeu à respecter, est que la projection se fasse parallèlement aux autres axes du repère. Si l'on est dans le plan, cela se réduit à : parallèlement à l'autre axe du repère. Tout vecteur se décompose ainsi de façon unique comme somme de deux (dans le plan) ou trois vecteurs, chacun parallèle à un axe de coordonnées.

3 . 2 . Base.

La liste des vecteurs unitaires, énoncée dans un ordre fixe, est aussi appelée une base de l'espace E. Nous pouvons nommer distinctement les vecteurs de base, par exemple , , . Nous pouvons aussi leur donner un numéro, dit indice. Ils seront alors appelés e₁, e₂, e₃. Les débutants préfèrent la première façon de nommer les vecteurs de base. Les professionnels préfèrent (de beaucoup) la seconde façon.

Il est possible de projeter tout vecteur sur les axes du repère.

Si on nomme , , , les axes de ce repère, on pourrait nommer , , , les trois projections de sur ces trois axes, = + + .

On peut rapporter chaque projection, au vecteur unitaire de cet axe. Soient V_x, V_y, V_z, les trois quotients :

= V_x

= V_y

= V_z

Tout vecteur de l'espace E est décomposable sur la base, d'une seule façon, que voici :

= V_j + V_k + V_l = V₁ e₁ + V₂ e₂ +V₃ e₃ .

Les nombres V_j , V_k , V_l (ou V₁ , V₂ , V₃ , puisque par définition, ce sont les mêmes) sont nommés coordonnées de sur cette base. Chaque coordonnée est donc bien un quotient. Un vecteur se distingue d'une grandeur physique ordinaire, scalable, et scalaire, en ce qu'il faut plusieurs quotients à la fois, pour le décrire. On a longtemps confondu la composante , avec la coordonnée V_x. Considèrant le vecteur , reliant l'origine au point M, les coordonnées de , sont identiques aux coordonnées du point M.

Si pendant quelque temps, on ne change jamais de base (repère et vecteurs unitaires), on économise en écritures, en se contentant de désigner un vecteur par seulement ses coordonnées dans cette base. On peut les écrire en ligne : (V₁ , V₂ , V₃), ou en colonne :

Oublier de mentionner la base, son unité et ses propriétés, est une omission trop courante. Cette négligence serait mortelle pour un calcul en cristallographie : tout serait faux. D'autant plus dangereuse qu'elle est tacite et inconsciente, cette négligence a vite produit de grosses incompréhensions, qui durent, qui durent... Ainsi, on s'est souvent imaginé qu'un vecteur ne serait rien de plus qu'une suite de nombres, en oubliant de l'accompagner de la règle de transformation de cette suite, à chaque changement de base, et d'une unité physique.

3 . 3 . Addition de vecteurs par les coordonnées.

Aucune difficulté : on additionne les coordonnées homologues.

Soient les vecteurs et , de coordonnées et (coordonnées sur la même base !).

Le vecteur somme + a pour coordonnées : .

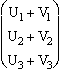Même scénario pour la différence : différence des coordonnées.

Changement d'origine, pour les vecteurs de repérage des points de l'espace. L'origine était O. Désormais on prend O'. On applique la règle d'addition des bipoints : .

3 . 4 . Multiplication par un nombre, ou une constante "scalaire".

On multiplie toutes les coordonnées par la constante.

4 .1 Généralisations :

4 . 1 . espaces vectoriels abstraits.

Ces deux lois, d'addition, et de multiplication par un "scalaire" (au sens du mathématicien : tout élément du corps, R ou C), ont ensuite été généralisées, pour former les axiomes de base d'une classe d'objets mathématiques très généraux, les espaces vectoriels.

Ce qui est moins bien, et dommageable, c'est qu'étant à court de termes, on a appelé vecteurs, les éléments de n'importe quelle sorte d'espace vectoriel; amalgamant deux concepts bien différents, sur des degrés d'abstraction incompatibles. Ce qui a encore ajouté aux confusions déjà banalisées dans les esprits, surtout chez les gens hostiles à l'axiomatique, et réticents à hiérarchiser leurs concepts. Pour quelques paresses de vocabulaire, ce fut le règne calamiteux du n'importe-quoi-pourvu-qu'on-calcule.

4 . 2 . Grandeurs concrètes et grandeurs physiques.

La particularité, du point de vue du mathématicien, est qu'il s'agit ici d'une généralisation à rebours, se contentant de regarder à nouveau une notion de base apprise à l'école primaire, et maltraitée depuis :

On peut additionner toutes sortes de nombres. Mais on ne peut additionner des pots de fleurs avec des mètres de tranchées.

On peut multiplier toutes sortes de nombres. Mais multiplier une vitesse par une fréquence, ça ne donnera sûrement pas une longueur d'onde.

Les nombres sont tout-abstraits. Les grandeurs physiques sont semi-abstraites, et gardent une propriété du monde réel, dont les nombres sont dispensés : une signification, et la grammaire qui y est associée. Les grandeurs physiques sont dispensées des propriétés fort compliquées des mesures, et des résultats de mesures (avec toutes leurs sortes d'incertitudes et d'erreurs), et de celles du stockage de ce résultat sur un papier ou dans une machine électronique, avec ses problèmes de largeur limitée, d'où résolution et étendue limitées.

Pour les grandeurs concrètes, l'égalité a un sens, si l'on sait définir un protocole de comparaison et de mesure. Par exemple, comparer deux longueurs, comparer deux aires, ou comparer deux lots de paquets de lessive, sous fardelages différents. A ce prix, nous avons le droit d'écrire une égalité de grandeurs, sans unités homogènes, comme : 21 cm = 0,21 m.

La physique ayant vocation à traiter de grandeurs physiques, elle est donc inféodée au principe de covariance des lois physiques. Au moins pour toutes les lois macroscopiques, et même pour celles des lois quantiques, chaque fois qu'une des grandeurs est à spectre continu, non quantifié. Physicien, j'ai dû définir les grandeurs vectorielles par héritage à partir des grandeurs physiques simples, et non à partir des nombres.

5 . Symétries des vecteurs.

5 . 1. Géométrie sur une droite.

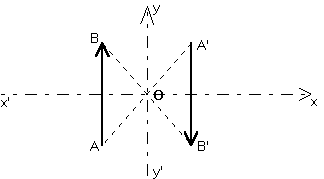
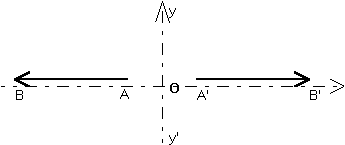
Symétrie par rapport à un point. Le vecteur est toujours retourné par cette symétrie.

5 . 2 . En géométrie plane (dans le plan)

Il ne peut y avoir que deux sortes de sous-espaces invariants par la symétrie : un point ou une droite. Le point est un sous-espace de dimension nulle. La droite est un sous-espace de dimension un.

Symétrie par rapport à un point. Le vecteur est toujours retourné par cette symétrie. Alors que les grandeurs de second échelon, telles que les angles orientés, sont conservées !
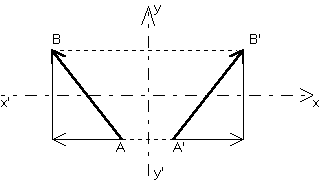
Symétrie par rapport à une droite. Deux cas simples se présentent : Le vecteur est parallèle à la droite invariante. Il est conservé.
Le vecteur est perpendiculaire à la droite invariante. Il est retourné.
Cas général : Vecteur ni perpendiculaire ni parallèle à la droite invariante. Alors la projection intérieure de V sur D est conservée, tandis que le restant, projection extérieure, est retourné.

5 . 3 . Géométrie dans l'espace E₃ (affine à R³).

Il ne peut y avoir que trois sortes de sous-espace invariant par la symétrie : un point, une droite, ou un plan. Le plan est un sous-espace de dimension deux.

Symétrie par rapport à un point. Le vecteur est toujours retourné par cette symétrie.

Symétrie par rapport à une droite. Deux cas simples se présentent :

Le vecteur est parallèle à la droite invariante. Il est conservé.

Le vecteur est perpendiculaire à la droite invariante. Il est retourné.

Cas général : vecteur ni perpendiculaire ni parallèle à la droite invariante. Alors la projection intérieure de V sur D est conservée, tandis que le restant, projection extérieure, est retourné.

Symétrie par rapport à un plan. Deux cas simples se présentent :

Le vecteur est parallèle au plan invariant. Il est conservé.

Le vecteur est perpendiculaire au plan invariant. Il est retourné.

Cas général : vecteur ni perpendiculaire ni parallèle au plan invariant. Alors la projection intérieure de V sur le plan P est conservée, tandis que le restant, projection extérieure, est retourné.

Les dessins se déduisent immédiatement des dessins valides en géométrie plane. Pas d'éléments vraiment nouveaux. La symétrie par rapport à un plan se dessine en projection sur un plan, identiquement à la symétrie par rapport à une droite, si l'on choisit de projeter sur le plan qui contient les vecteurs symétriques.

5 . 4 . Généralisation, en espace de dimension n.

La projection intérieure d'un vecteur sur un sous-espace invariant, est conservée

La projection extérieure d'un vecteur sur un sous-espace invariant, est retournée.

5 . 5 . A quoi les symétries sont-elles utiles ?

Les symétries servent à ramener de nouveaux problèmes à des problèmes connus et déjà résolus. Elles servent à se simplifier la vie, à prouver que des coordonnées sont nulles, ou égales, sans longs calculs. Elles servent à prouver que des effets sont nuls. En 1894, Pierre Curie (1859 - 1906) a énoncé le principe : L'effet est au moins aussi symétrique que la cause. Réciproquement, c'est la dissymétrie qui crée le phénomène.

Il existe de nombreuses autres sortes de symétries, que nous n'étudions pas ici.

5 . 6 . Généralisation : échelon d'une grandeur.

L'échelon d'une grandeur physique, c'est la plus petite dimension d'espace vectoriel dans lequel elle puisse exister.

En échelon 1 : Les vecteurs et leurs inverses, les covecteurs; ils existent sur une droite.

En échelon 2 : Les angles orientés de 2 vecteurs, leurs produits extérieurs et tensoriels, et leurs inverses.

En échelon 3 : Les angles solides orientés, les volumes orientés, les densités orientées.

Etc.

La classe des scalaires réunit les vecteurs sur un espace de dimension un, les quotients de vecteurs sur un espace de dimension un[1], les quotients de tourneurs sur un espace de dimension 2, etc.

6 . Si on change de vecteurs de base ?

Supposons que je communique le résultat de mes travaux, à un ami et collègue ingénieur, qui travaille aux Etats Unis. Moi, j'ai travaillé en mètres, l'unité légale en France de nos jours. Mais lui travaille en yards, en pieds et en pouces. Ou plus simplement, je voudrais communiquer mes travaux à un physicien âgé, qui a utilisé toute sa vie le centimètre comme unité légale, utilisée par les physiciens du monde entier.

Je lui parle d'un vecteur long de 2 mètres. Pour me comprendre, il va traduire cela comme un vecteur long de 200 cm. Traduisons cela en coordonnées :

= (2,0,0) m = (200,0,0) cm.

On remarque que quand l'unité est 100 fois plus grande, alors les coordonnées sont 100 fois plus petites. Autrement dit, les coordonnées naturelles sont contravariantes : elles varient au contraire de la base. C'est indispensable, pour que ces coordonnées désignent bien le même vecteur physique.

7 . Grandeurs vectorielles en physique.

La somme vectorielle, sous la forme d'addition de vitesses, ou d'addition de forces, était maîtrisée dès le 17e siècle, par certains physiciens (pas tous...). Malgré ce que nos manuels nous font croire, ni Laplace (1749 - 1827), ni Ampère (1775 - 1836) n'ont connu le mot "vecteur", inventé en 1837, ni les notations vectorielles.

7 . 1 . Unités de base de la physique.

On peut rapporter toutes les unités de la physique, à un tout petit nombre d'unités de base, huit en tout :

L'unité de longueur (mètre), qui ne suffirait pas à la géométrie, sans...

le radian, quotient de deux longueurs perpendiculaires. Le radian est le grand oublié des physiciens. Sa généralisation comme quotient de deux grandeurs en quadrature de phase, n'a jamais été clarifiée.

L'unité de temps (seconde),

l'unité de masse (kilogramme),

l'unité de charge électrique (coulomb).

On peut symboliser ces cinq unités de base par les cinq majuscules : L, R, T, M, Q.

Les trois autres, le kelvin, la candela, la mole, ne nous serviront pas ici.

Chaque unité physique particulière, s'exprime comme un monôme généralisé des unités de base. Monôme généralisé, signifie : expression ne comportant que des multiplications et divisions. Les multiplications ou divisions multiples, peuvent se résumer par une élévation à une puissance. Cette puissance peut être négative, pour désigner une division. Par exemple, l'unité de vitesse, le mètre par seconde, a pour monôme : [L . T^-1].

Cet exposé est très classique. Nous verrons ultérieurement à quel point il est critiquable, et doit être révisé de fond en comble au regard de la mécanique symplectique, et du théorème de Noether.

7 . 2 . Quelles sont les grandeurs physiques qui sont vectorielles ?

Nature de la grandeur	Unité S.I.	Monôme dimensionnel
Déplacement	m	[L]
Vitesse	m/s	[L.T^-1]
Accélération	m/s²	[L.T^-2]
Impulsion (quantité de mouvement)	kg . m /s	[M.L.T^-1]
Force	kg . m /s²= newton	[M.L.T^-2]
Champ électrique ()	volt/mètre = newton/coulomb	[M.L.T^-2.Q^-1]
Moment dipolaire électrostatique	C . m	[L.Q]
Elément de courant (C'est le I.dl figurant dans la loi de Laplace).	A . m = C . m /s	[L.T^-1.Q]
Potentiel magnétique () [2]	unité d'impulsion/coulomb	[M.L.T^-1.Q^-1]

Comment se relient-elles à la translation ?

Opération	genre translation	Multiplier par masse		genre impulsion
	déplacement
Diviser par durée	vitesse		quantité de mouvement
Diviser par durée	accélération		force

Opération	genre translation	Multiplier par charge électrique		genre courant
	déplacement		Dipôle électrique
Diviser par durée	vitesse		élément de courant
Diviser par durée	accélération

Opération	genre impulsion	Diviser par charge électrique		genre champ E. M.

Diviser par durée	quantité de mouvement		Potentiel magnétique
Diviser par durée	force		Champ électrique

On peut rassembler ces trois tableaux partiels en un seul, plus compliqué :

Opération	genre champ	multiplier par charge électrique		Diviser par masse		Multiplier par charge électrique		genre courant
					déplacement		Dipôle électrique
Diviser par durée	Potentiel magnétique		Impulsion		vitesse		élément de courant
Diviser par durée	Champ électrique		force		accélération

Les covecteurs sont les grandeurs de dimensions en [L^-1], qui ont les mêmes propriétés de symétrie que les vecteurs (mais qui en diffèrent évidemment par leurs propriétés dimensionnelles). Plusieurs gradients considérés en chimie (lois de diffusion moléculaire ou ionique), ou en mécanique des fluides et en météorologie, sont des covecteurs, inverses de vecteurs. Vecteurs et covecteurs, composent la famille de premier échelon.

7 . 3 . Pour pouvoir profiter en physique de la géométrie vectorielle,

il faut séparer les unités physiques, telles qu'on vient de les rapporter aux unités de base, en deux sous-monômes : une partie qui ne contient que la longueur, et une partie qui contient toutes les autres unités de base. Par exemple : [L . T^-1] = [L ].[ T^-1]

Si le sous-monôme longueur (la partie réservée à la seule unité du genre longueur, élevée à une puissance entière relative quelconque), est de degré un, autrement dit est exactement L, alors cette grandeur physique peut probablement être rattachée à la géométrie des vecteurs.

La règle simpliste énonçant que seules les grandeurs physiques, où la longueur intervient par une puissance nette 1, ou -1, peuvent être vectorielles, est violée par les cas de densités vectorielles volumiques qui sont en [L^-2]. Par exemple, la densité volumique de dipôles électriques (utile pour caractériser le diélectrique dans un condensateur, ou pour décrire l'espace autour d'une antenne) :

Vecteur de déplacement de Maxwell ( = $\epsilon$ ) : [L^-2 . Q] = [L . L^-3. Q].

Nous reviendrons aux cas plus délicats, tels que le "vecteur de Poynting" qui n'est guère vectoriel que dans le vide, dans l'article consacré au lien entre caractère géométrique, et dimension physique.

Si de plus, après analyse des faits, le physicien vérifie que cette grandeur décrit bien quelque chose d'orienté dans l'espace, et si ce genre d'orientation est exactement de la même espèce qu'un vecteur (il y a d'autres manières, dont la plupart sont plus compliquées), avec les mêmes symétries expérimentales, il pourra conclure que cette grandeur physique est vectorielle.

On nomme covecteurs les grandeurs de dimensions en [L^-1], qui ont les mêmes propriétés de symétrie que les vecteurs (mais qui en diffèrent évidemment par leurs propriétés dimensionnelles). Plusieurs gradients considérés en chimie (lois de diffusion moléculaire ou ionique), ou en mécanique des fluides et en météorologie, sont des covecteurs. En physique, il est cohérent de considérer que la famille des grandeurs vectorielles au sens large, contient les vecteurs et les covecteurs. Le théorème de Noether nous donnera la raison définitive de ce regroupement en une seule famille.

7 . 3 . 1 . Rappel : définition d'un modèle. Un système A, est dit modèle d'un système B, si en regardant A au lieu de B, je peux répondre aux questions que je me pose sur B.

7 . 3 . 2 . En conséquence, nous n'aurons raison de qualifier de vectorielle une grandeur physique, que si, en utilisant les propriétés des vecteurs, énoncées plus haut dans cette leçon, nous savons tout du comportement géométrique de cette grandeur physique. Autrement dit, si la géométrie vectorielle, est bien un modèle de la géométrie de la grandeur physique en question. Et notre grandeur physique n'est pas seule au monde : elle est en relation géométrique avec d'autres grandeurs physiques. Cela restreint notre fantaisie.

Evidemment, si une grandeur physique, n'a pas tout à fait le comportement géométrique d'un vecteur, par exemple, n'en a pas les symétries, ou n'en a pas le comportement dimensionnel (cf. § 13), alors elle n'est pas vectorielle ! Quelles que soient les bévues historiques cristallisées vers 1888, il faut choisir : le produit de deux vecteurs ne peut pas être, lui aussi, un vecteur ! Ou si un produit est un vecteur, alors soit le multiplicande, soit le multiplicateur, n'est pas un vecteur. Il faut choisir, sous peine d'absurdités en cascade.

L'Histoire nous apprend que chaque fois que voir les grandeurs physiques orientées fut problématique, les privant de leur instinct kinésique, certains physiciens ont balancé, entre les interpréter comme vecteurs (vrais vecteurs, polaires[3]), ou comme êtres de rotation. L'exemple le plus célèbre est Faraday (mais aussi Œrsted dès 1821, Wollaston, Helmholtz en 1856, Kirchhoff vers 1860)[4], pour qui le champ magnétique, était polaire puisqu'il pouvait voir les spectres magnétiques, tandis que le courant dans un fil pouvait aussi bien être un vortex, puisqu'il ne pouvait pas le voir. Malheureusement, là, Faraday avait tout faux. André Marie Ampère, William Thomson à partir de 1856, puis James Clerk Maxwell, adoptèrent la position inverse, seule correcte. Thomson et Maxwell tenaient compte de l'expérience de polarisation rotatoire magnétique de la lumière, et de l'électrolyse. Pierre et Jacques Curie tranchèrent à nouveau la question de la symétrie du champ électrique, à partir de 1883, grâce à leur découverte de 1881: la piézoélectricité.

8 . Module d'un vecteur. Contracté du produit intérieur, ou produit scalaire.

8 . 1 . Module, ou norme, d'un vecteur.

8 . 1 . 1 . Définition

Le "module" (ou "norme", ou "longueur" chez E. Cartan, voire "intensité" dans les L.P.), généralise la longueur, pour toutes les sortes de vecteurs. Pour un vecteur de déplacement, dans l'espace euclidien de notre expérience courante, ce module est exactement la longueur du bipoint, mesurée avec un double-décimètre. Le module exprime ce qui est invariant envers l'orientation par rapport aux axes de coordonnées.

Plus généralement, le module satisfait aux trois axiomes des normes :

= pour tout λ réel (ce qui implique : = 0).

< + inégalité triangulaire.

Ces deux premiers axiomes sont aussi remplis par les pseudo-normes, des espaces pseudo-euclidiens, tels l'espace de Minkowski. L'axiome suivant est caractéristique des vraies normes :

> 0 pour tout vecteur non nul.

La physique exige de plus que l'expression analytique de ce module, donne un résultat intrinsèque indépendant du choix des coordonnées, et des unités. Un résultat invariant, ni covariant, ni contravariant, INVARIANT. Le module d'un vecteur physique n'est donc pas un simple nombre, mais est une grandeur physique. Il a donc une unité physique, par exemple des mètres. Pendant très longtemps, les conséquences de cette exigence basique n'ont pas été perçues[5].

8 . 1 . 2 . Calcul du module d'un vecteur.

8 . 1 . 2 . 1. Calcul en dimension 1: le long d'une droite.

Il nous suffit de savoir le module de l'unité : , car = v . , donc = v . .

Si on change d'unité, par exemple en prenant 100 fois plus petit, la coordonnée v devient 100 fois plus grande, pour maintenir l'invariance.

8 . 1 . 2 . 2 . Calcul en dimension 2 : sur un plan.

8 . 1 . 2 . 2 . 1 . Cas simple : le repère est orthonormal.

Autrement dit = , et ces deux vecteurs sont perpendiculaires.

On peut alors utiliser le théorème de Pythagore, sans précautions.

= v_j . + v_k . = v . cos θ. + v . sin θ . = v ( cos θ . + sin θ . ), et on utilise la propriété d'invariance de la longueur envers l'orientation du vecteur par rapport aux axes de coordonnées. La seule fonction invariante, exprimée en fonction de cos θ et de sin θ , est la somme de leurs carrés. Donc

= v . = v . = .

8 . 1 . 2 . 2 . 2 . Cas moins simple : le repère est orthogonal.

Les deux vecteurs et sont perpendiculaires, mais leurs modules ne sont pas égaux. ≠ 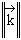. Ce cas est courant sur les cartes de géographie, ou pour le repérage d'un avion en vol : les distances au sol sont en kilomètres, et l'altitude est en mètres.

Les projections d'un vecteur sur les axes de coordonnées gardent les mêmes propriétés, gardent la même longueur. Prenons l'exemple d'un vecteur, dont les projections orthogonales mesurent 500 m et 1,2 km. Il suffit de convertir 1,2 km en 1200 m, et de reconnaître un triangle de Pythagore (5; 12;13), pour avoir son hypoténuse sans calculs : 1300 m, ou 1,3 km. En effet 13² = 169 = 144 + 25 = 12²+ 5². Nous aurions piteusement échoué avec des coordonnées prises sans précautions à 500 et 1,2, comme de simples nombres.

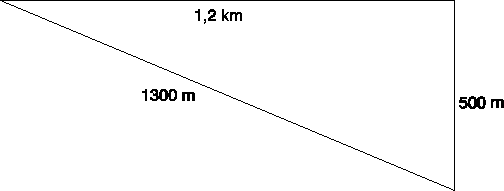
Conclusion pour le cas du repère orthogonal : = v_j² + v_k² .

8 . 1 . 2 . 2 . 3 . Encore moins simple : le repère est quelconque. Nous devrons attendre d'avoir traité le cas du module du produit intérieur (son premier invariant), ou produit scalaire de deux vecteurs.

8 . 1 . 2 . 3 . Calcul en dimension 3 : dans l'espace ordinaire.

Même scénario qu'en dimension 2. Juste une coordonnée à ajouter.

8 . 1 . 2 . 3 . 1 . Cas simple : le repère est orthonormal. Trois vecteurs unitaires , , et perpendiculaires, et de même module : = = . On peut alors utiliser le théorème de Pythagore, sans précautions.

= v_j . + v_k . + v_l . . Donc = v . = (v_j² + v_k²+ v_l²) .

8 . 1 . 2 . 3 . 2 . Cas moins simple : le repère est orthogonal.

Les trois vecteurs , , et sont perpendiculaires, mais leurs modules ne sont pas égaux.

= v_j² + v_k² + v_l² .

8 . 2 . Le produit scalaire de deux vecteurs (contracté du produit intérieur).

8 . 2. 1. Terminologie.

On s'écarte ici de la terminologie d'Elie Cartan[6], qui n'orthogonalisait pas la différence sémantique entre produit extérieur et produit intérieur. Or le produit extérieur (produit tensoriel antisymétrisé) d'une grandeur d'échelon n et d'une grandeur d'échelon m, est d'échelon n+m. La régularité du vocabulaire oblige à garder le même comportement dimensionnel au produit intérieur, qui se confond donc avec le produit tensoriel symétrisé; à un coefficient numérique éventuel près. Ces deux sortes de produits préservent l'associativité.

Alors que le "produit scalaire" n'est pas associatif. Ce n'est donc pas du tout un vrai produit.

8 . 2 . 2 . Définition.

Pour tenir la route, la définition doit être donnée en grandeurs physiques, en non en coordonnées. En effet, les coordonnées n'ont de signification qu'à partir des propriétés des vecteurs de base. , où désigne la longueur, ou le module, du vecteur . Cette définition est intrinsèque, et découle de la projection intérieure.

Au temps où l'on confondait allègrement les grandeurs physiques avec les nombres, on prenait le "produit scalaire" pour un nombre, et c'était la source de confusions et de mésaventures sans fin.

Evidemment, un nombre multiplié par le carré d'une longueur, n'est pas un nombre, mais une grandeur scalable, de dimension homogène à une aire de surface.

8 . 2 . 3 . Usages.

En physique, le produit scalaire (contracté du produit intérieur), sert surtout à calculer le travail d'une force :

force déplacement cosinus (force; déplacement).

Autrement dit, avant de multiplier la force par le déplacement, on commence par projeter l'un sur l'autre, et la projection est orthogonale. C'est bien la projection intérieure qui est utilisée ici. Puis on prend le produit des modules.

En géométrie, le contracté du produit intérieur sert à calculer des angles, et des longueurs.

En électricité, dans l'espace abstrait de Fresnel (le complexifié de la droite réelle), le "produit scalaire" (en fait, la partie réelle du produit hermitien) sert à calculer la puissance moyenne (ou puissance active), et le facteur de puissance. A tout instant, la puissance instantanée reçue par un récepteur est le produit de la tension aux bornes, par l'intensité, avec l'orientation convenable des signes. Si le déphasage est très proche de π/2, ce récepteur est un miroir pour la puissance : il restitue durant un quart de période la puissance reçue durant le quart de période précédent. Ces renseignements, plus la phase de la puissance instantanée, sont aussi obtenus en détails par le produit intérieur (tensoriel symétrisé). Toutefois la tradition, par héritage-confusion des nombres complexes, a ignoré le produit intérieur, n'apercevant que son contracté, que l'on doit alors compléter par le produit extérieur (qui, en dimension 2, n'a qu'un seul degré de liberté).

8 . 2 . 4 . Piège :

Pour que le produit scalaire soit un nombre, il faut qu'un vecteur soit en mètres, et l'autre en m^-1. Autrement dit, seul le produit scalaire d'un vecteur par un covecteur (ou l'inverse, puisque ce produit est commutatif), peut donner un nombre.

A quoi bon ces subtilités byzantines ? grognent les collègues, on sait tout ça depuis longtemps... Voire.

Ce que savent les collègues depuis longtemps, n'est que ce qu'on a pensé à leur enseigner : une somme de produits de coordonnées, incapable de respecter l'exigence d'invariance.

Ce piège date des disciples de Hamilton, inventeur des quaternions en 1843, qui ont extrait du produit de quaternions, la composante "scalaire", nommée produit scalaire, et la composante alors considérée comme "vectorielle", qu'ils ont appelée produit "vectoriel" (Stokes et Tait en ont déduit le rotationnel vers 1849). Or cette école britannique ne savait pas distinguer un vecteur de ses coordonnées (une vague liste de nombres), ni un nombre d'une grandeur. D'où la somme de produits de coordonnées qu'on vous a enseignée, en oubliant que les coordonnées n'ont de signification qu'à partir des propriétés des vecteurs de base.

De même que vous avez appris à parler vers deux ans, et n'avez appris la grammaire que bien plus tard. Ils ont appris à écrire il y a longtemps, mais peu de nos élèves ont une orthographe correcte. Les mathématiciens et les physiciens aussi, mettent longtemps, ici plus de cent cinquante ans, à mettre de l'ordre dans leur langage, dans leur écriture, dans la mise en forme de leurs théories. Ils esquivent leurs tâches de grammairiens, et se dérobent à la création d'un contrôle qualité, capable de représenter les intérêts des clients contre les paresses et les abus du producteur.

8 . 2 . 5 . Propriétés du produit scalaire (contracté du produit intérieur).

On utilise la définition : .

Ce produit conserve évidemment la multiplication par un nombre : = .

Il conserve aussi l'addition, donc la projection et la décomposition en projections sur les axes de coordonnées. Cela se déduit de la linéarité de l'opérateur de projection : la projection sur un axe, de la somme de deux vecteurs, est la somme des projections de ces vecteurs sur le même axe. On en conclut que le produit scalaire est distributif sur les opérations de somme vectorielle, et de multiplication par un nombre.

La contraction brise l'associativité, qui était conservée par le produit tensoriel, et par la symétrisation.

8 . 3 . Expression du produit scalaire avec les coordonnées.

Soient , , , les trois vecteurs de base. Les longueurs j, k, l, sont les modules de ces vecteurs , , . Les angles ( ,), (,), (, ) sont notés α, β, γ.

8 . 3 . 1 . Expression simplifiée, en repère orthonormé.

Les angles , , sont supposés droits, donc leurs cosinus sont tous nuls. Donc les produits scalaires suivants sont nuls :

. = 0, . = 0, . = 0, . = 0, . = 0 . = 0.

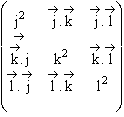
Les trois autres sont unitaires par hypothèse :

. = j² = unité au carré. . = k² = unité au carré. . = l² = unité au carré.

= V_j + V_k + V_l

' = V'_j + V'_k + V'_l

On utilise alors la distributivité :

.' = (V_j + V_k + V_l ) . (V'_j + V'_k + V'_l ) = V_jV'_j j² + V_k V'_k k² + V_l V'_l l².

Les termes croisés étant affectés de coefficients nuls. D'où : .' = (V_jV'_j + V_k V'_k + V_l V'_l ) unité².

8 . 3 . 2 . Expression complète avec les coordonnées.

Pour l'expression générale, on est amené à calculer, pour chaque système de vecteurs de base, un tableau carré g, où sont portés les produits scalaires de chaque vecteur de base, par chaque vecteur de base.

g = =

Cela s'appelle le tenseur métrique, ou plus anciennement, la matrice de Gram (au sens des mathématiciens, en oubliant l'unité physique). Une base est orthonormale, si et seulement si sa matrice de Gram est la matrice unité.

D'où le carré du module d'un vecteur : = . = .

Ceci peut se réinterpréter comme le premier invariant du produit tensoriel , qui est d'ailleurs le même que celui du produit symétrique . La seconde interprétation est à préférer, premier invariant du produit symétrique, car elle s'étend plus proprement au produit scalaire de deux vecteurs : = .

Ce nom de "tenseur" est encore un de ces hasards cocasses de l'Histoire. Il se trouve que le premier physicien à s'emparer des outils de "calcul différentiel absolu" de Gregorio Ricci-Curbastro et de Tullio Levi-Civita, fut Woldemar Voigt, qui en avait l'usage pour décrire l'élasticité des cristaux.

Par un hasard similaire, un chant guerrier composé à Strasbourg pour l'armée du Rhin, devint ensuite "la Marseillaise". Il n'y a aucune espèce de "tension" à interpréter dans "tenseur", ni rien de marseillais dans notre hymne national. Il n'y a là rien de plus que le premier utilisateur qui ait été vraiment remarqué.

9 . Changements de base.

9 . 1 . Expression matricielle des changements de base.

Cette expression découle directement de la définition des vecteurs comme classes d'équivalence des bipoints. Elle généralise ce que nous avons vu de la covariance et de la contravariance, rappelé dans l'article précédent. Ecrivons les coordonnées des nouveaux vecteurs de base, selon l'ancienne base : et , puis assemblons ces colonnes de coordonnées en un tableau carré, appelé matrice de changement de base :

, à 2 dimensions. 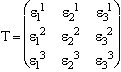, à 3 dimensions.

Que notre espace vectoriel soit de dimension 2, 3, 4 ou 77, le principe est le même.

Nous pouvons calculer la matrice inverse T^-1, telle que T^-1.T= T.T^-1 = 1.

T^-1 est la matrice qui exprime l'ancienne base en fonction de la nouvelle. Nous avons déjà vu au § 7, que les coordonnées d'un vecteur sont contravariantes à la base : un vecteur est du genre longueur. On pourrait le dire en style plus savant, mais cela n'apporterait rien de plus. Donc c'est la matrice T^-1 qui transforme les anciennes coordonnées d'un vecteur dans les nouvelles (le même vecteur, exprimé selon la nouvelle base) :

Soit un vecteur quelconque, exprimé dans l'ancienne et la nouvelle base (dimension 3 ou n, qu'importe) :

= V_j + V_k + V_l = V¹ e₁ + V² e₂ +V³ e₃ = V'¹ ε₁ + V'² ε₂ +V'³ ε₃ .

A partir de cet instant, on s'imposera la discipline de n'écrire les coordonnées contravariantes qu'avec des indices en haut. Il faudra ne pas confondre avec l'écriture des puissances d'un nombre.

A. Einstein (1879-1955) a condensé cette écriture, par la convention que tout indice répété en haut et en bas, signifie une sommation sur cet indice. Réécrivons selon la convention d'Einstein :

= Vⁱ e_i = V'^j ε_j .

Or, par définition de T, ε_j = Tⁱ_j e_i. Donc = Vⁱ e_i = V'^j ε_j = V'^j Tⁱ_j e_i . On peut validement simplifier par les vecteurs de base.

Il vient : Vⁱ = V'^j Tⁱ_j . C'est à dire les anciennes coordonnées en fonction des nouvelles. Nommons τ ⁱ_jles coordonnées de la matrice inverse T^-1. On peut alors exprimer les nouvelles coordonnées en fonction des anciennes : V'ⁱ = V^j τ ⁱ_j .

Les covecteurs ont le comportement dimensionnel opposé, soit exactement celui des vecteurs de la base : la matrice T change les anciennes coordonnées en les nouvelles.

Tels sont le comportement dimensionnel des vecteurs, et celui des covecteurs. Ce comportement est caractéristique, et ne connaît aucune exception. Si les coordonnées d'une grandeur ont un autre comportement envers un changement de base que celui d'un vecteur (respectivement : d'un covecteur), alors elle n'est pas un vecteur (resp. : un covecteur).

Cette règle est consubstantielle à la physique macroscopique.

Bien que Cayley ait bien établi l'algèbre des matrices de changements de base, dans les années 1850, les physiciens n'ont commencé à s'en apercevoir qu'au 20e siècle, après M. Grossmann, A. Einstein et E. Cartan.

Visiblement, E. Whittaker (1873-1956), cité dans l'article précédent, n'avait toujours pas perçu en 1951 cette propriété caractéristique. Dans son six-vector hétérogène, les trois coordonnées du champ électrique sont contravariantes par rapport à l'unité de longueur[7]. Tandis que les neuf coordonnées du champ magnétique, sont une fois covariantes, et une fois contravariantes par rapport à l'unité de longueur (outre qu'elles sont contravariantes à l'unité de temps). Il faut une fois la matrice T, et une fois la matrice T^-1 pour calculer les nouvelles coordonnées magnétiques dans un changement de base. Mais Whittaker n'imaginait que des repères orthonormés. Or, dans le cas particulier du seul espace tridimensionnel, et dans le cas particulier où cet espace tridimensionnel n'est rapporté qu'à des repères orthonormés, ces neufs coordonnées se réduisent à six coordonnées non nulles, qui sont opposées deux à deux. Ce qui donne alors l'apparence de seulement trois coordonnées strictes. D'où le calembour trop enseigné : "Trois composantes, alors c'est un vecteur !"...

L'enquête a montré là que toute la collectivité des physiciens a dépendu de la lenteur d'A. Einstein à tout assimiler des implications de la grammaire tensorielle, alors qu'il était le seul physicien à faire ce travail indispensable. Dans ses articles de 1916, il n'a pas encore créé sa "convention d'Einstein". Il emploie encore le ronflant “Viertervektor” pour désigner un vecteur dans la dimension 4, et “Sechservektor (antisymmetrischen Tensor zweiten Ranges)”[8] pour désigner un tenseur antisymétrique de rang 2. Einstein n'est devenu cohérent qu'en 1921, alors que le mathématicien Hermann Weyl (1885-1955) est au clair sur ce point dès 1918 (formé à Göttingen, lui n'avait aucun compte à rendre aux traditions absurdes des physiciens).

9 . 3 . Garde-fou dimensionnel.

Reprenons l'exemple d'un vecteur de l'espace affine ordinaire : = V_j + V_k + V_l . Il est naturellement rapporté à des vecteurs unitaires de base, qui sont eux-mêmes rapportés à une unité de longueur. Ces vecteurs unitaires sont donc exprimés en mètres. Tandis que les coordonnées (contravariantes) de notre vecteur sur ce repère, ne sont que des nombres.

Les composantes du tenseur métrique g, sont donc exprimées en mètres carrés, leur unité naturelle. Les composantes du tenseur métrique réciproque sont donc en m^-2. Le covecteur inverse de s'exprime naturellement sur la base duale (contravariante), qui est en m^-1 : . = 1.

Il est devenu habituel de considérer sans précautions une seconde expression possible : exprimer en fonction de la base duale, et inversement, le vecteur dual en fonction de la base directe. Mais alors les nouvelles coordonnées cessent aussitôt d'être des nombres sans dimension.

Sur la base duale (contravariante, en m^-1), les coordonnées (covariantes) de sont en m². Si l'on passe en unités cm, les coordonnées sont alors divisées par 100 : ce sont des cm². Tandis que les coordonnées naturelles (contravariantes) sont multipliées par 100.

Résumons : 2 m = 2 x1 m = 200 x 1 cm = 200 cm² x 1 cm^-1 = 2 m²x 1 m^-1.

Nous avons bien vérifié sur les coordonnées covariantes : 200 cm² = 2 m²/100.

Sur la base directe (en m), les coordonnées du dual de sont en m^-2. Si l'on passe en unités cm, les coordonnées sont alors multipliées par 100. Tandis que les coordonnées naturelles sont divisées par 100.

Résumons : 0,5 m^-1 = 0,5 x 1 m^-1 = 0,005 x 1 cm^-1 = 0,005 cm^-2 x 1 cm = 0,5 m^-2x 1 m.

Nous avons bien vérifié sur les coordonnées contravariantes : 0,005 cm^-2 = 0,5 m^-2x 100.

Et pourtant, depuis Elie Cartan, tout le monde croyait malin de répéter cet énorme barbarisme dimensionnel : "En repère orthogonal, la distinction entre composantes covariantes, et composantes contravariantes disparaît"[9]. Autrement dit : 200 = 200 cm². Et 5 = 5 cm^-2. Ahurissant. Tout est prêt pour l'affirmation : "5 flacons = 5 pétroliers", ou pour le calcul de l'âge du capitaine en additionnant les chèvres avec les oies.

9 . 3 . Livret de famille des tenseurs sur un espace vectoriel (de dimension n) :

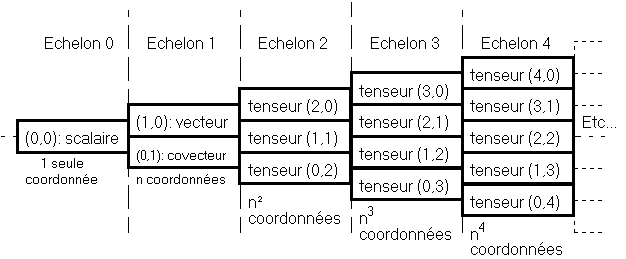
Si le comportement des coordonnées d'une grandeur, ressemble à celui des coordonnées d'un vecteur ou d'un covecteur, en ce sens qu'il faut appliquer n fois la matrice de changement de base, et p fois la matrice inverse, alors cette grandeur appartient à la famille plus générale des tenseurs, ici n fois covariant, p fois contravariant, ce qui se note : de type (p, n).

Nous venons de citer le tenseur métrique, sous la forme de type (0,2) : coordonnées 2 fois covariantes.

Avant éventuelle contraction, le produit d'un vecteur par un covecteur, est de type (1, 1). Le produit de deux vecteurs est de type (2, 0). Le produit de deux covecteurs est de type (0, 2). La contraction d'un type (1, 1) a pour résultat un type (0, 0), scalaire. Sur un espace vectoriel de dimension n, un tenseur d'ordre p, a exactement n^p coordonnées. Mais des conditions de symétrie peuvent en restreindre l'indépendance.

Plus généralement, le dual (au sens algébrique, seul cohérent) d'une grandeur physique, a toujours les mêmes propriétés de symétrie. Pour l'instant, nous ne l'avons constaté que pour les vecteurs et leurs duaux, les covecteurs. Nous verrons ensuite le lien étroit avec la dimension physique, et avec le théorème de Noether.

9 . 4 . Garde-fous abstraits, garde-fous concrets, garde-fous sociaux.

Nous avons rencontré jusqu'ici les garde-fous suivants :

Des garde-fous abstraits : la règle syntaxique de changement des coordonnées selon les changements de base. Les règles des symétries. Des règles de cohérence entre la signification spécifiée, et la propriété algébrique d'associativité ou non. La cohérence des unités physiques, ou cohérence dimensionnelle.

Les garde-fous concrets : l'épreuve expérimentale. Y compris l'épreuve d'enseignement.

Un garde-fous sémantique, qui est d'abord pratique, et social ensuite. Le codage d'allure mathématique (donc intimidant pour beaucoup), devient sûr, et devient vraiment vérifiable, si on a accepté d'en écrire préalablement la signification expérimentale, en langage clair, accessible au plus grand nombre. Il est si facile de se tromper seul. Il est si facile de tromper la poignée d'élèves dociles qui dépendent de votre bon plaisir pour obtenir son examen final [10]. Si vous supprimez tout repère sémantique, vous restreignez outrageusement le public capable de vous relire, de comprendre vos erreurs, et de vous corriger. Et vous supprimez du même coup la plupart des critères qui permettraient de repérer ce qui correct, et ce qui s'est égaré.

Aucun de ces garde-fous ne doit être hypostasié, ni déifié. Ni plus jamais méprisé non plus.

10 . Dans le prochain article,

nous traiterons des grandeurs géométriques qui, bien qu'indispensables à la physique élémentaire, ne sont pas des vecteurs : la vitesse angulaire, l'accélération angulaire, la vitesse aréolaire, le moment angulaire, le champ magnétique, le moment magnétique, le flux magnétique.

La façon habituelle aux physiciens, de modéliser ces grandeurs, leur a donné auprès des mathématiciens sérieux, une réputation peu enviable, de désinvolture et d'incohérence. Réputation très en dessous de la réalité, car elle ne tenait pas compte de l'incohérence dimensionnelle pratiquée : chez les physiciens, tantôt l'unité physique d'une de ces grandeurs tornatorielles tenait compte du radian (rarement), tantôt elle l'oubliait (le plus souvent). Cet oubli du radian permettait des exploits, comme d'entasser le travail et le moment d'un couple dans la même case dimensionnelle; et quelques autres du même ordre.

Nous montrerons les moyens de mettre enfin en ordre la discipline que nous enseignons. Cela soulagera nos élèves : ils n'auront plus à croire des incroyables, comme ces lois tout en travers, bravant leur expérience physique, ces lois à la chiralité absurde, et inexplicablement référantes à l'anatomie des mains des primates homo sapiens. Ils seront enfin délivrés de l'obligation farfelue de dessiner dans l'espace pour représenter le rotationnel d'un mouvement plan... Ils pourront enfin se fier à une grammaire simple, structurée, et qui n'est plus encombrée d'exceptions systématiques. Ils n'auront plus à corriger à la main les fautes de symétries invariablement introduites par le pseudo-outil incorrect que la paresse de leurs aînés nous a imposé jusqu'ici.

Ils ne seront plus tentés de confondre les deux états de spin d'un photon, avec deux directions de polarisation plane de la lumière, comme des vulgarisateurs chevronnés en physique le font parfois[11].

Auteur : Jacques Lavau

[1] Faut-il créer une catégorie spéciale pour les scalaires strictement positifs, tels que la température, la masse ?

[2] Inventé par F. E. Neumann en 1845, puis par W. Thomson en 1847. Maxwell le lui empruntera vers 1862.

[3] Michel Hulin écrivait: vecteurs de bonne foi. Il les opposait à ceux de mauvaise foi. B.U.P. 572 (1975).

[4] Histoire Générale des Sciences. P.U.F. PARIS 1961.

[5] Ceci n'est guère exprimé avant E. Cartan (1869 - 1951), et encore, de façon très partielle et insuffisante.

[6] Reprise aussi par W. Penrose & W. Rindler, Spinors and space-time. Cambridge university Press 1984.

[7] T 2, p. 163, lignes 2 et 3, p. 193 l. 4, il affirme l'identité d'un tenseur antisymétrique, avec un six-vector. Chapitre 5, il ramène plusieurs auteurs, dont David Hilbert, Gustav Mie, Minkowski, Einstein, Kottler, dans son six-vector.

[8] A. Einstein; Eine neue formale Deutung der Maxwellschen Feldgleichungen der Elektrodynamik. Prüss. Akad. Sitz. 1916. pp 184-188.

[9] Elie Cartan; Leçons sur la géométrie des espaces de Riemann. Gauthier-Villars, Paris 1946. Réed. Gabay, 1988 Paris.

[10] Tous autant que nous sommes, nous avons en commun d'avoir été de dociles élèves abusés. La question qui nous sépare, est d'accepter ou non d'abuser à notre tour de la confiance, de la crédulité (et de l'ambition) de nos élèves.

[11] Incroyable mais vrai: cf. F. David Peat; Superstrings and the Search for the Theory of Everything. p 250-251. Contemporary Books. Chicago 1988.

Syntaxe géométrique de la physique : projections et vrais vecteurs.