Syntaxe
géométrique de la physique : démêlage
linguistique préalable.
Auteur : Jacques Lavau
1 .
Prérequis généraux.
1 .1 .
Définition d'un "modèle".
1 . 2 .
Analogie.
2 .
Démêlage linguistique :
qui a besoin de quel concept ?
2 . 1.
Les signes comme moteur ? Les significations comme freins ? Ou
l'inverse ?
2 . 2 .
Collisions inévitables, collisions évitables.
2 . 2 . 1 .
Collisions phonétiques.
2 . 2 . 2 .
Entassements de concepts sous un même morphème.
2 . 3 .
La polysémie de "vecteur" : quatre ou cinq
usages. Ou huit ?
2 . 3 . 1 .
Les prolégomènes oubliés.
2 . 3 . 2 .
Les usages à délimitation immédiatement
correcte.
2 . 3 . 3 .
Les usages confus, à démêler.
2 . 3 . 4 .
Synthèse de l'inventaire des significations de tous les
"vecteurs" prétendus.
3 .
Un vecteur, comme son nom l'indique, c'est pour les
translations,
3 . 1.
Définition : de la translation, à la classe
d'équipollence des bipoints.
4 .
Quatre projections pour la physique.
Une troisième projection :
"dioptrique", ou "anti-intérieure".
Quatrième projection :
anti-extérieure.
5 .
Suite
Auteur : Jacques Lavau
Syntaxe géométrique
de la physique : démêlage linguistique préalable.
Auteur : Jacques Lavau
1
.
Prérequis généraux.
1 .1 . Définition
d'un "modèle".
Un système A, est dit modèle d'un système
B, si en regardant A au lieu de B, je peux répondre aux
questions que je me pose sur B.
Il en résulte que la qualification de A comme
modèle, dépend de l'ensemble des questions que je me
pose sur B. Plus je me pose de questions, plus je serai
exigeant sur le choix du modèle.
Il est clair, que substituer au système B, un
modèle, n'a d'intérêt, que si on y trouve un vrai
avantage. Par exemple, ce sera parce que c'est moins cher, ou plus
rapide, ou plus accessible, ou moins dangereux. Etc.
1 . 2 . Analogie.
Pour l'analogie, on n'est pas exigeant. On se contente de
remarquer qu'il y a eu des situations où A ressemblait
à B. Et comme on connaît A bien mieux que
B, on s'habitue à en pifométrer l'extrapolation
au chic : entre A, et B qu'on
distingue encore mal, la ressemblance est présumée
s'étendre sans limites.
Facile, et instinctive, l'analogie est indispensable dans de
nombreux cas, pour chercher à connaître et à
comprendre. Elle est aussi trompeuse, et très dangereuse :
on oublie trop souvent de vérifier ses limitations. Il faut
savoir dépasser le temps du flou heuristique. Se permettre
l'analogie, impose de vérifier après, si elle était
valide. Se permettre la paresse de négliger cette
vérification, c'est prendre le risque de pratiquer
l'imposture.
L'outil mathématique, comme analogie de la réalité
physique, est trop rarement suspecté, très peu
questionné, et bien mal traité. Notamment, trop de
physiciens ont abusé des vecteurs comme analogies non
vérifiées. Et presque personne n'osa rectifier. Trop
longtemps, les auteurs de manuels s'autorisèrent à
changer subrepticement de définition des vecteurs, toutes les
trois pages, sans que personne osât broncher.
2
.
Démêlage linguistique
: qui a besoin de
quel concept ?
2 . 1. Les signes comme moteur
? Les significations comme freins ? Ou l'inverse ?
Actuellement, les mathématiciens vivent sur une
success-story usée : celle du développement
historique de l'algèbre, par le dynamisme des symboles, malgré
les réticences de ceux qui répugnaient à donner
une signification aux nombres négatifs, et a fortiori
aux nombres complexes. De nos jours, ils abusent à fond de
l'autonomie des signes, et du jonglage avec les signes, en refusant
obstinément de s'intéresser à la syntaxe et à
l'algèbre des significations. Le balancier est bloqué à
fond du côté du dernier succès reconnu.
Or l'expérience prouve que les significations pratiques, et
la syntaxe des significations, sont choses trop sérieuses pour
qu'on les abandonne aux seuls praticiens. Certains - trop - s'y
enferment n'importe comment, marquent le territoire à
l'instinct, et stérilisent le métier pendant des
générations. Je m'attacherai donc à restaurer
une dialectique saine et complète entre le jeu des signes et
le jeu des significations et des applications, et entre tous
les métiers intervenants. La dialectique entre les
intervenants est condition indispensable à toute politique de
qualité, et elle doit être largement garantie, avant
même que d'être rationalisée.
2 . 2
.
Collisions inévitables, collisions évitables.
Les possibilités du cerveau humain ont depuis longtemps
dépassé les possibilités de la phonétique.
La première conséquence a nargué les
linguistes : les collisions phonétiques. La seconde
conséquence nous nargue tous les jours dans notre métier
de professeurs : les entassements et collisions de concepts sous
un même mot.
2 . 2 . 1
.
Collisions phonétiques.
Tous les jours, le linguiste rencontre des homonymes exacts pour
des concepts presque confondus, dans des langues éloignées,
sans aucun contact entre elles depuis très longtemps, parfois
plusieurs dizaines de milliers d'années, par exemple entre
l'hébreu et une langue andine. Pendant longtemps, les
malheureux linguistes se sont escrimés à proposer des
explications, en forme de migrations préhistoriques à
travers les océans... Jusqu'à ce qu'on s'aperçoive
que le nombre des phonèmes articulables par l'espèce
humaine est limité, que chaque peuplade n'en emploie
nécessairement qu'un sous-ensemble réduit, et que le
nombre de mots, phonétiquement praticables, de peu de
syllabes, qu'on peut former à partir de ces phonèmes,
n'est pas bien grand. Que donc ces collisions sont statistiquement
bien prévisibles, et que dans bien des cas, il n'y a
strictement rien à interpréter.
2 . 2 . 2
.
Entassements de concepts sous un même morphème.
Les morphèmes existant dans notre langue, sont en nombre
réduit, quelques dizaines de milliers, et chacun d'entre nous
n'en maîtrise qu'une toute petite minorité. La création
de néologismes est un art peu et mal pratiqué. La
réactivation de mots corrects, mais tombés en
désuétude, est un art presque inconnu, et qui se heurte
à des tabous, à des haines et des mépris
difficiles à justifier.
Or, le besoin en concepts est quotidiennement énorme. Tous
les jours, la réalité nous force à en créer,
ou recréer faute de savoir que la création avait déjà
été faite ailleurs. Il n'est pas rare de rencontrer une
quinzaine de significations entassées sous un seul morphème
(morphème : la forme extérieure du mot, le fait d'être
composé de telles lettres, à prononcer de telle façon).
Statistiquement, les collisions sémantiques, sont un
événement très fréquent, beaucoup plus
fréquentes qu'elles ne le seraient si nous étions moins
paresseux, plus attentifs, et plus compétents.
Aussi, nos élèves butent tous les jours sur les
polysémies bizarres que nous leur transmettons sans y
réfléchir : un même mot véhicule de
nombreuses significations d'un jour à l'autre, d'un lieu à
l'autre, dont personne ne les a avertis. Personne n'a crié
gare au changement de contexte, de tradition locale, d'idiome local à
une profession ou à une école de pensée. Chaque
groupuscule, chaque despote local, a des prétentions à
considérer le restant de l'espèce comme autant de
sous-hommes, contre lesquels l'arme de son incivisme serait légitime,
et imbu de sa juste idiosyncrasie, s'arroge le privilège
d'ignorer les collisions sémantiques avec les autres
professions utilisatrices des mêmes mots.
2 . 3
.
La polysémie de "vecteur" : quatre ou cinq usages.
Ou huit ?
2 . 3 . 1
.
Les prolégomènes oubliés.
Bien qu'on définisse les espaces vectoriels abstraits
assez tard dans les études, au début des études
supérieures, nos bambins manipulent dès l'école
primaire, dès le CE2 pour être précis, des
membres d'espaces vectoriels de dimension 1: les grandeurs
concrètes, et les grandeurs physiques (autres que
vectorielles, ni tensorielles). Puis, l'enseignement secondaire étant
disloqué entre spécialités étrangères
les unes aux autres, nos potaches oublient tout, aux mains de matheux
purs, qui n'entendent rien à la physique. Ils s'installent
alors durablement dans la confusion entre nombres et grandeurs.
Nous allons avoir besoin de caractériser ces grandeurs
pratiques et concrètes d'une part (par exemple 500 flacons
d'un médicament), et ces grandeurs physiques d'autre part, par
leur lien avec une grandeur unité, et avec l'ensemble des
nombres réels. Nous allons donc définir les grandeurs
scalables. Nous aurons aussi besoin de distinguer entre les
grandeurs arbitrairement scalables, et les grandeurs
nombrables, pour lesquelles existe une unité absolue
définie par la nature, et non par une société
humaine.
2 . 3 . 1 . 1
.
Grandeurs scalables.
Par définition, on peut les rapporter à une unité
: elles sont le produit d'une grandeur-unité par un nombre
réel.
Par conséquent, si l'on change l'unité de mesure
d'une grandeur scalable, le quotient de cette grandeur (par exemple
un prix) par son unité est contravariant à cette
unité. Dans les classes primaires, ce nombre quotient est
désigné comme "le nombre exprimant la mesure de
...", ce qui est trop lourd. Dans les espaces de dimension
supérieure à 1, chacun de ces quotients, serait désigné
comme "composante", ce qui ici, serait prématuré.
Il faut trouver mieux pour ce stade. Je suggère :
"multiplicateur", ou "quotient".
Exemples : On peut s'acquitter d'une dette de mille francs, avec
deux billets de 500 F, ou vingt billets de 50 F. On peut expédier
60 tonnes de marchandises, par 3 camions de 20 tonnes, ou par 2
camions de 30 tonnes. Cette page mesure en large 21 cm, ou 210 mm, ou
0,21 m. 21 cm = 0,21 m : le quotient est contravariant. Quand
l'unité est 100 fois plus grande, alors le quotient est 100
fois plus petit. Autrement dit, les quotients varient au
contraire de l'unité de base, afin d'avoir compétence
à désigner la même grandeur.
Schéma : Grandeur scalable = quotient x
grandeur-unité.
Et si l'unité est composée ? Si l'essence est à
5,60 F le litre, et que le dollar est à 5,60 F, alors
l'essence est à 1$ le litre : contravariance. Mais elle est à
3,785 $ par gallon, ou encore à 21,20 F par gallon, puisqu'un
gallon vaut 3.785 litres : covariance. Ce prix par unité
de volume, varie comme l'unité de volume.
Le nombre qui exprime ce prix de l'essence, est covariant à
l'unité de capacité : il grandit ou rapetisse comme
elle. Ce nombre est contravariant à l'unité monétaire
: il grandit ou rapetisse à l'envers de l'unité
monétaire. Bizarrement, ces mots de covariance et de
contravariance, n'étaient entendus qu'en fin d'études
supérieures, alors que les phénomènes désignés,
sont rencontrés dès les classes primaires. Rencontrés,
mais ignorés dès le passage dans l'enseignement
secondaire. C'est une lacune regrettable, car les notions de variance
sont le coeur même de la mesure et de la physique. Cette
syntaxe des unités physiques, a presque toujours été
sous-estimée[1].
Les mathématiciens n'ont jamais daigné s'y intéresser,
et trop de physiciens sont trop inadvertants pour en tirer toutes les
conséquences.
2 . 3 . 1 . 2 . Grandeurs
arbitrairement scalables.
C'est a priori le cas de la plupart des grandeurs de la
physique, comme la longueur. Dans le domaine macroscopique, il n'y
avait aucune raison de choisir le mètre-étalon de cette
longueur plutôt que d'une autre (rappelons-nous le pied de
Charlemagne). Pourtant, en physique quantique, on a envie depuis
longtemps, de définir une longueur élémentaire,
ou de rapporter toutes les longueurs à la constante de
Rydberg. Mais cela ne permettra jamais de définir toutes les
longueurs comme des multiples exacts de ladite constante de Rydberg,
ni même d'une hypothétique longueur élémentaire.
Paradoxalement, il est possible de définir de façon
intrinsèque l'inverse d'une grandeur arbitrairement scalable.
Notre seul postulat est de disposer d'un protocole de comparaison,
permettant de conclure à l'égalité de deux
échantillons d'une grandeur physique, ou à une
inégalité dans tel rapport. Supposons un tel résultat
: A = B. Il devient alors non-absurde de réécrire ce
résultat : A/B = 1, et même 1/B = A-1.
Evidemment, le quotient de A-1 sur l'unité-inverse,
est aussi arbitraire que le quotient de A sur l'unité
directe, mais leur produit (quotient x unité) est bien une grandeur physique invariante envers
l'unité de mesure. Il est à remarquer que nous n'avons
pas eu besoin de disposer d'un protocole de mesure sur l'espace des
grandeurs inverses.
Vérifions que ceci est bien invariant envers les unités.
Une longueur a vaut 2 mètres, ou 200 cm. Son inverse
a-1 vaudra 0,5 m-1. Ou 0,005 cm-1.
Son quotient est bien contravariant à l'unité inverse,
ou covariant à l'unité directe. L'invariance de a-1
est bien assurée.
En poursuivant ce raisonnement, nous voyons que nous n'aboutissons
à aucune contradiction algébrique, à définir
toutes les puissances entières relatives d'une grandeur
scalable, et de ses unités de mesure possibles. A . A-1.
= 1 permet de conclure que : A . A . A-1. = A, ou : A2
. A-1. = A.
2 . 3 . 1 . 3 . Grandeurs
nombrables : scalables par une constante universelle.
En physique, on rencontre dans cette classe des grandeurs
nombrables :
la charge électrique, que l'on rapporte à la charge
élémentaire de l'électron ou du proton (on peut
descendre si l'on y tient, à la charge élémentaire
d'un quark).
Le moment angulaire intrinsèque, qui est toujours multiple
demi-entier de h = 1,05457266 . 10-34 joule.seconde/radian.
L'action maupertuisienne (et non l'action hamiltonienne), qui est
toujours multiple entier de h.
Le flux magnétique dans un supraconducteur, multiple de
h/2q.
Contre-exemples : La masse atomique d'un noyau ou d'un atome ne
ressemble qu'approximativement à une grandeur nombrable. Elle
serait nombrable sans le défaut de masse, reponsable de la
stabilité du noyau. Ce n'est qu'une grandeur indiçable,
à deux indices, sur les numéro atomique Z et nombre
total de nucléons A. Toutes les vitesses de groupe, qui sont
inférieures à la célérité limite
de propagation de l'énergie dans le vide c.
Il va de soi qu'outre l'unité naturelle, on peut toujours
définir des unités arbitraires, pour la commodité.
Pour la charge électrique, les électriciens préfèrent
le coulomb à la charge élémentaire, trop petite
pour leurs gestes de métier. Pour les flacons de médicament,
l'usine livre aux grossistes par unités insécables de
plusieurs flacons, peut-être 24. Il y aura peut-être une
période de jonction où cohabiteront deux emballages
différents, et deux unités de facturation différentes
: par 24 flacons, ou par 30. Une commande de 2400 flacons, sera
satisfaite aussi bien par 100 cartons de 24, que par 80 cartons de
30. Telle est la vie pratique. Les notions de covariance et de
contravariance continuent de s'appliquer aux grandeurs nombrables :
elles restent scalables.
2 . 3 . 2
.
Les usages à délimitation immédiatement
correcte.
2 . 3 . 2 . 1
.
En premier, depuis des millénaires, nous rencontrons l'usage
littéral : est vecteur ce qui véhicule quelque
chose. Une flèche incendiaire tirée depuis un arc à
corde très lâche, fut un vecteur de combustion, capable
de provoquer un incendie dans les fortifications en bois de
l'adversaire. Au 18e siècle, les colporteurs furent les
vecteurs des pamphlets révolutionnaires. Certaines fusées
sont des vecteurs nucléaires. Le moustique est le vecteur de
la fièvre jaune et du paludisme.
Rappel de vocabulaire : Le mot "vector" était
déjà pris depuis plus de 42 siècles, avant
d'être réutilisé en 1837 par W. R. Hamilton (1805
- 1865), à l'usage des mathématiciens et des
physiciens. Dans le dictionnaire de latin, on trouve une famille de
plus de 100 termes autour du verbe "vehere", des
noms "vector" (au sens de chariot, puis d'animal
bâté ou de trait, de cavalier ou de passager d'un
navire), et "veha" (voie). En français, nous
avons gardé : véhicule, voie, dévier,
convecteur, vexer, convexe, vétérinaire. La famille est
également riche dans les langues germaniques : Weg,
thalweg, Norvège, Solveig, tramway,
wagon, vaguemestre.
2 . 3 . 2 . 2
.
En second, nous rencontrons sa mathématisation immédiate
(mais correcte), pour les besoins de la physique macroscopique : est
vecteur ce qui caractérise une translation. Ce cahier des
charges est rempli par la définition de Bellavitis : les
vecteurs comme classes d'équivalences des bipoints par la
relation d'équipollence. La sémantique précédente
est donc conservée, dans ses grandes lignes, mais connaît
une schématisation. Du point de vue mathématique, et
dans le langage axiomatique que nous devons aux écoles de
Klein et de Hilbert, nous avons besoin des axiomes des espaces
vectoriels, plus une métrique, plus le moyen de définir
une translation. Ce qui implique que l'espace en question soit au
moins approximable localement par un espace affine pseudo-euclidien
tangent. Du point de vue pratique, cela signifie que l'on peut
valablement dessiner, et se servir de ses mains, d'une règle,
d'un compas, d'une équerre, ou de ses pas, ou de ses outils
d'atelier, pour se guider dans les raisonnements.
Par extension légitime, est aussi considéré
comme vecteur, tout ce qui dérive du vecteur de translation,
par une dérivation ou intégration selon une variable
qui n'est pas d'espace (le temps, notamment), ou par multiplication
par une grandeur, dont la dimension physique ne comprend aucune
longueur, à quelque puissance que ce soit.
|
2 . 3 . 2 . 3
. En troisième lieu, nous rencontrons les
éléments de tout espace vectoriel abstrait, quel qu'en soit la
signification, ou le vide de sens, avec ou sans métrique.
En algèbre, on ne
demande à un espace vectoriel abstrait, que d'être un groupe commutatif
pour une opération, usuellement notée "+", et d'être stable pour une
opération externe, appelée multiplication par les éléments d'un certain
corps K, auquel aucune autre particularité n'est demandée que d'être un
corps algébrique.
Toutefois, cela
implique des propriétés, comme celles des projections sur des
sous-espaces vectoriels, l'existence de bases, de la décomposition
unique sur une base, et des lois de changement des composantes
selon les changements de base, afin de conserver invariante une
éventuelle signification. Très simples, ces lois n'ont été énoncées et
comprises que très tard, et restent encore lettre morte pour la
majorité des enseignants concernés. Nous suggérons de désigner par le
terme "vectoroïdes" les éléments d'un espace vectoriel abstrait.
|
|
2 . 3 . 3
.
Les usages confus, à démêler.
2 . 3 . 3 . 1
.
Trois sans lois. C'est l'état sauvage et archaïque
du second concept, venant du 19e siècle qui ne pratiquait que
des composantes cartésiennes, et se méfiait de toute
démarche géométrique intrinsèque. Par
paresse mathématique, on ("on" : disciples
maxwelliens, Heaviside) a édicté que tout ce qui n'est
pas vecteur, et qui n'est pas vraiment nombre, est quand même
vecteur. Notamment les rotations infinitésimales.
On s'est donc dispensé de toute espèce de définition
qui soit mathématique - car quelle qu'elle soit, on la viole
constamment (à chaque "produit vectoriel",
notamment). On se contente d'avoir un usage, qui est en
usage dans la peuplade. Pour eux, il suffit d'avoir une liste de
nombres, appelées composantes, sans aucune loi de changement
de base, car on ne veut pas savoir changer de base. On tient bien à
l'addition des vecteurs, et à la multiplication par un
scalaire, mais on en refuse les conséquences inévitables,
et se dispense des contraintes qui en découlent. On se permet
le plus souvent d'être incohérent avec l'opération
de projection sur un sous-espace vectoriel, et a fortiori,
avec l'immersion dans un espace de dimension supérieure. Il
arrive même qu'on se dispense de toute homogénéité
dimensionnelle entre lesdites composantes.
Dans la suite, nous désignerons ce concept "laxeur",
car il est caractérisé par son laxisme.
Techniquement, c'est un record, plus ou moins hétérogène.
Sémantiquement, son intention est tantôt de désigner
un vrai vecteur, tantôt le record homogène compacté
d'un tenseur d'un ordre non précisé (souvent un tenseur
antisymétrique de rang 2), plus rarement un record hétérogène,
représentant par exemple les trois constantes de l'équation
d'une droite du plan : aX + bY + c = 0, voire quelque
chose d'encore plus hétérogène.
2 . 3 . 3 . 2
.
N'importe quelle liste de nombres, Cet usage se rencontre en
mécanique quantique : un vecteur d'état. On l'a
aussi rencontré parfois en micro-informatique, où un
vecteur n'était autre qu'un pointeur, vers une routine
vitale, comme la routine d'initialisation à l'allumage, ou
celle d'erreur mortelle.
Cette fois, il n'est même plus question d'addition ni de
multiplication : une liste, rien d'autre.
On peut rencontrer des cas logiquement différents : la
liste chaînée, de longueur a priori inconnue, le
record structuré, mais dont la structure est mystérieusement
connue et attendue, par des moyens externes, et la suite, indexée
sur un ensemble dénombrable. Les espaces de Banach reposent
sur de telles suites, indexées sur un ensemble dénombrable,
ou non.
2 . 3 . 3 . 3 . N'importe quelle
liste de nombres, structurée : ce qu'on appelle en
informatique un RECORD.
Certains peuvent bien être, simple question de hasard, des
composantes de vecteurs, d'autres sont des indicateurs booléens,
ou des numéros d'un type logique énuméré,
des numéros de méthode pour le programme qui va
utiliser et interpréter ce RECORD. D'autres champs du record
peuvent être occupés par tout autre chose que des
nombres.
Simplement, dans un RECORD, il ne faut pas s'attendre à ce
que la méthode d'utilisation des champs successifs, soit
uniforme. Soit que chaque nature et chaque méthode est
convenue d'avance, soit que chaque champ porte un drapeau qui signale
sa nature, et le type de méthode qui sera compétent.
La sémantique diffère, donc la méthode de
conception du programme, donc aussi la méthode de test, et le
jeu de test seront qualitativement différents. Et en
pédagogie, la stratégie didactique comme les méthodes
pédagogiques seront nécessairement distinctes, selon le
type logique des champs du RECORD.
Par exemple, je peux très bien considérer 4,5 m.s-1
comme un record, composé d'un nombre "4,5", d'un
exposant implicite "1" sur l'unité physique "mètre",
d'un exposant "-1" sur l'unité physique "seconde",
et d'exposants implicites "0" sur les autres unités
fondamentales du système d'unité alors en usage. C'est
du ressort de ma liberté individuelle. Toutefois, si je vous
prétendais que ceci est un vecteur, de dimension au moins 3,
vous me traiteriez immédiatement de farfelu, et vous auriez
raison. Or, ce n'est pas plus ni moins farfelu que de traiter les 9
composantes d'un tenseur antisymétrique de rang 2, de
"vecteur" en dimension 3... Là tout s'est
passé comme si, en traitement algébrique de la
géométrie, on n'avait pas encore conquis le chiffre
zéro. Comme si, trois composantes nulles - dans
certains repères privilégiés seulement - c'était
comme rien, ce qui autoriserait à un traitement
elliptique et obscur. Depuis 152 ans, nous n'osons torcher une "Quick
and Dirty Physics", vite et mal torchée, où
l'on confond analogie avec modèle, nombre avec grandeur
physique, etc...
2 . 3 . 3 . 4
.
Les prévecteurs : complexes et hypercomplexes.
Qu'ils soient de dimension 2, 4, ou 8 sur le corps des réels,
les nombres complexes, les quaternions, et les octaves de Cayley, ont
une propriété en commun : tout changement d'unité
ou de base est incongru et impossible. On est totalement prisonniers
de la définition algébrique, avec un élément
neutre de l'addition, qui est zéro, que l'on ne peut
translater nulle part ailleurs. Et avec un élément
neutre de la multiplication, qui est 1, que l'on ne peut multiplier
par rien d'autre, sauf à ce qu'il ne soit plus élément
neutre. En revanche, les prévecteurs forment toujours un
ensemble clos, envers l'addition et envers la multiplication par un
nombre, ou par un prévecteur.
2 . 3 . 3 . 5
.
Collision sémantique à résoudre :
scalaire
Cette notion de "scalaire", peu définie, ou
tacitement non-définie, enjambe la confusion entre nombres et
grandeurs. Elle a un pied de chaque côté. D'où
d'autres solides confusions. Il faut trancher.
Pour les mathématiciens qui définissent des espaces
vectoriels abstraits, le "scalaire" est un élément
du corps (le plus souvent commutatif) sur lequel on peut pratiquer
des multiplications externes. Le "scalaire" n'est
donc qu'un nombre (entiers, réels, complexes, ou
hypercomplexes, n'importe pas ici), ou un substitut de nombre, par
exemple un membre d'un corps fini.
Pour les physiciens, est "scalaire" une grandeur
qui n'est pas vectorielle, ni tensorielle, ni
tensorielle-déguisée-en-vecteur-de-fiction. Or ces
acceptions sont incompatibles, et quelqu'un doit renoncer à
son acception. Après avoir expérimenté les deux
actions possibles, je constate bien moins coûteux d'interdire
"scalaire" dans l'acception "membre d'un corps"
(car les mathématiciens ne manquent pas de substituts), que
d'obliger les physiciens à adopter un néologisme. Nous
préciserons donc ultérieurement notre définition
: est scalaire, une grandeur physique scalable, qui par projection
dans l'espace accessible, n'a qu'un seul degré de liberté.
Définition entièrement relative à la dimension
de l'espace accessible. Il s'est révélé
impossible de maintenir aucune espèce de définition
absolue. Dans un espace de dimension 1, le quotient de deux vecteurs
est un scalaire; c'est faux en dimension 2 et au delà. Dans un
espace de dimension 2, le quotient de deux tourneurs est un scalaire;
c'est faux en dimension 3 et au delà. Dans un espace de
dimension 3, le quotient de deux capacités est un scalaire;
c'est faux en dimension 4 et au delà.
2 . 3 . 4 .
Synthèse de l'inventaire des significations de tous les
"vecteurs" prétendus.
|
|
Vecteur qui véhicule.
|
Vrai vecteur géométrique et physique.
|
Elément d'espace vectoriel abstrait.
|
Trois sans lois.
|
N'importe quelle liste de nombres.
|
|
Nature des composants, ou "champs".
|
|
Grandeurs physiques homogènes
|
Nombres, ou non précisé.
|
Grandeurs physiques.
|
N'importe quoi.
|
|
Sémantique
|
Transport, comme sur un chariot
|
Caractériser une translation
|
Néant
|
Contradictoire
|
Néant
|
|
Addition, multiplication par scalaire
|
|
OK
|
OK
|
OK
|
Néant
|
|
Algèbre : règle de covariance
|
|
OK
|
OK
|
Astuces d'évitement de l'obstacle
|
Néant
|
|
Cohérence avec sous-espaces, et sur-espaces
|
|
OK
|
OK
|
Refusé
|
Néant
|
|
Symétries géométriques
|
|
OK
|
OK
|
Contradictoire
|
Néant
|
|
Métrique
|
|
OK
|
Ajoutable
|
Contradictoire
|
?
|
|
Physique : règles dimensionnelles
|
|
OK
|
Ignoré
|
Parfois
|
Néant
|
|
Qui l'utilise ?
|
Public cultivé, biologistes, militaires, etc.
|
G. Bellavitis, H. Weyl, A. Einstein.
|
Mathématiciens, certains physiciens théoriciens
|
Physiciens, techniciens
|
Des snobs ?
|
|
Qui sait l'utiliser avec sécurité ?
|
Public cultivé, biologistes, militaires, etc.
|
Vous, demain
|
Mathématiciens
|
Certains d'entre les physiciens
|
?
|
|
Qui en a besoin ?
|
Tout le monde : logistique, biologie.
|
Tous physiciens, tous techniciens.
|
Mathématiciens, physiciens
|
Personne
|
Nul n'a besoin de désigner une liste par un autre vocable que
"liste".
|
|
Désignation proposée :
|
Vecteur
|
Vecteur
|
Vectoroïde
|
Laxeur
|
Liste
|
Agrandissons
la zone des trois-sans-lois, pour en mieux discerner le détail,
et ses liens avec le voisinage :
|
|
Tenseur sur un espace vectoriel ou affine.
|
Record homogène, compacté d'un tenseur.
|
Record homogène
|
Record hétérogène
|
Liste
|
|
Nature des composants, ou "champs".
|
Nombres ou grandeurs physiques homogènes.
|
En général des réels
|
Tous des entiers, ou tous des réels.
|
Nombres, champs logiques et énumérés.
|
N'importe quoi.
|
|
Sémantique
|
Selon rang du tenseur.
|
Empruntée à ce tenseur
|
? ? ?
|
A détailler selon la nature des champs.
|
A découvrir sur place.
|
|
Addition, multiplication par scalaire
|
OK
|
OK
|
Probablement sans objet.
|
Néant
|
Néant
|
|
Algèbre : règle de covariance
|
OK
|
A emprunter manuellement au tenseur signifié
|
Probablement sans objet.
|
Néant
|
Néant
|
|
Cohérence avec sous-espaces, et sur-espaces
|
OK
|
Impossible
|
Impossible
|
Contradictoire
|
Néant
|
|
Symétries géométriques
|
OK
|
Impossible
|
Impossible
|
Contradictoire
|
Néant
|
|
Métrique
|
OK
|
A emprunter manuellement au tenseur signifié
|
? ? ?
|
Contradictoire
|
|
|
Physique : règles dimensionnelles
|
OK
|
Possible, mais hasardeux
|
? ? ?
|
Contradictoire
|
Néant
|
|
Qui l'utilise ?
|
|
Physiciens, techniciens
|
Mathématiciens
|
|
|
|
Qui sait l'utiliser avec sécurité ?
|
|
Certains d'entre les physiciens
|
Mathématiciens
|
|
|
|
Qui en a besoin ?
|
Toute la Physique
|
Personne
|
Mathématiciens, physiciens
|
|
|
|
Désignation proposée :
|
Rang 1: vecteur, covecteur.
Rang 2, antisymétrique : Tourneur
Tenseur, sinon.
|
Laxeur
|
Record
|
Record
|
Liste
|
Selon ce tableau, il faut considérer
les six composantes du "Sechstervektor" qu'utilisait
encore A. Einstein en 1916[2],
et que Whittaker a utilisé jusqu'à la fin de sa vie
("Six-vector"), comme des records hétérogènes[3].
De même toutes les représentations usuelles des
"torseurs", se caractérisent par leur hétérogénéité.
Sans même mentionner que ce concept de "torseur" sert
à confondre les grandeurs mécaniques avec les
propriétés des solides indéformables,
incassables, et indéchirables. Et que ça n'est guère
un bénéfice. On y perd notamment le théorème
des travaux virtuels, et toutes ses applications à prédire
la stabilité et les oscillations.
3
.
Un vecteur, comme son nom l'indique, c'est pour les translations,
et c'est pour tout ce qui se déduit directement des
translations, en physique : vitesse, accélération,
quantité de mouvement, force, champ électrique, dipôle
électrostatique, vitesse de diffusion ionique.
3 . 1. Définition :
de la translation, à la classe d'équipollence des
bipoints.
Le cahier des charges est de caractériser l'opérateur
de translation. La définition formelle répondant à
ces réquisitions, définit le vecteur comme classe
d'équivalence de bipoints, par la relation
d'équipollence. Cette définition n'est
pas la définition minimaliste des espaces vectoriels
abstraits. Mais c'est la plus petite qui couvre toutes les propriétés
géométriques réellement utilisées par la
physique élémentaire classique.
Nos nombres entiers, si familiers, sont aussi des classes
d'équivalence : 2 n'est pas une paire de vaches, ni une paire
de cailloux, mais est ce qu'il y a de commun à une paire de
vaches, une paire de cailloux, une paire de claques, etc. par la
relation : {il existe une bijection entre ces deux collections}.
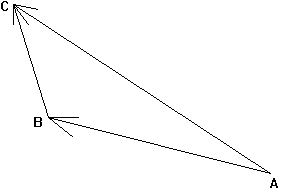
Dans un espace E, comme notre espace ordinaire de la géométrie,
les bipoints servent à résumer un déplacement,
avec un point de départ, et un point d'arrivée.
Un bipoint : c'est un couple de points, respectivement le premier,
ou point de départ, et le second, ou point
d'arrivée. On le note (A,B). Les extrémités
d'intervalles finis sur une droite, forment de tels bipoints.
|
On peut définir
une addition : si le départ du second, est exactement l'arrivée
du premier,
(A,C)
= (A,B) + (B,C).
Exemple : se
rendre de Paris à Lyon, puis de Lyon à Marseille, revient à se rendre
de Paris à Marseille. Puisqu'on ne s'intéresse qu'au point de départ,
et au point d'arrivée.
On ne sait pas
multiplier un bipoint par une constante. Mathématiquement, autant dire
qu'on ne sait presque rien faire avec des bipoints.
|
|
Ajoutons l'hypothèse que dans notre espace E, le postulat
d'Euclide soit vérifié : la parallèle d'une
droite passant par un point, existe, et est unique[4].
Dans ce cas, les parallélogrammes existent.
|
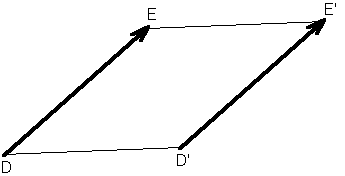
Définition :
Les bipoints (D,E) et (D',E') sont dits équipollents si le
quadrilatère DEE'D' est un parallélogramme.
De l'addition
des bipoints, on déduit l'addition des vecteurs : pour tous points
A, B, et C,
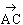 = =
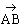 + +
 . .
C'est la relation
de Chasles.
|
|
Disons-le autrement : dans un espace euclidien, et grâce aux
parallélogrammes, on peut transporter les extrémités
d'un bipoint, les éléments caractérisant une
translation. Plus tard, pour parler d'orthogonalité, nous
aurons besoin de choisir une norme euclidienne parmi toutes celles
possibles.
La relation d'équipollence est une relation d'équivalence,
ce qui par définition, veut dire trois choses :
que (A,B) est équipollent avec lui même.
Que si (A,B) est équipollent à (C,D), (C,D) est
équipollent à (A,B).
Que si (A,B) est équipollent à (C,D), et que (C,D)
est équipollent à (E,F), alors (A,B) est équipollent
à (E,F).
Donc les bipoints (A,B) et (C,D) équipollents sont deux
représentants valide du même vecteur :
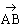 =
=
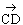 .
.
On peut donc choisir ou déplacer comme on veut les
représentants d'un ou de plusieurs vecteurs, pour rendre les
calculs faciles, ou simplement possibles.
Si les points A et B sont confondus, le vecteur
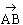 est
le vecteur nul.
est
le vecteur nul.
Maintenant, on peut toujours associer un vecteur à une
translation dans l'espace E.
On peut additionner des vecteurs de E quelconques, en nombre
quelconque, dans un ordre quelconque. On dit la même chose
autrement, en disant que l'addition des vecteurs est associative et
commutative. Tout vecteur a un opposé :
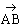 +
+
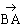 =
0. (déplacement nul)
=
0. (déplacement nul)
Par généralisation de l'addition de vecteurs
identiques, on peut donc multiplier des vecteurs par un entier
quelconque.
Inversement, en utilisant le théorème de Thalès[5],
on démontre facilement qu'on peut aussi diviser un vecteur par
un entier quelconque. Il en résulte qu'on peut multiplier un
vecteur par un nombre rationnel quelconque, et aussi diviser, par un
rationnel quelconque non nul.
Nous rappelant les propriétés de R (Q
est partout dense dans R), on admettra qu'on peut multiplier
tout vecteur par un nombre réel quelconque, par exemple
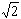 ,
qui n'est pas rationnel [6].
Le corps des nombres réels R, est appelé
"corps[7]
des scalaires" pour notre espace des vecteurs. Nous verrons au
chapitre des composantes, pourquoi ce baptême "scalaire",
qui évoque une échelle.
,
qui n'est pas rationnel [6].
Le corps des nombres réels R, est appelé
"corps[7]
des scalaires" pour notre espace des vecteurs. Nous verrons au
chapitre des composantes, pourquoi ce baptême "scalaire",
qui évoque une échelle.
4
.
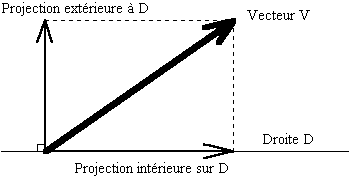
Quatre projections pour la physique.
Puisque nous savons faire la somme et la différence de deux
vecteurs, nous pouvons nous poser le problème
|
suivant :
Soient une droite
D, et un vecteur
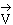 .
Peut-on décomposer le vecteur .
Peut-on décomposer le vecteur
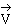 en
deux parties, une qui serait parallèle à D, nommée par exemple en
deux parties, une qui serait parallèle à D, nommée par exemple
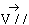 ,
et une autre ? ,
et une autre ?
|
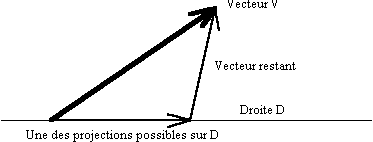
|
Jusqu'ici, notre problème admet une infinité de
solutions. En particulier, dans le cas où D et
 sont
perpendiculaires, il y a une solution plus simple que toutes les
autres : prendre
sont
perpendiculaires, il y a une solution plus simple que toutes les
autres : prendre
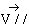 nul.
nul.
Il faut donc nous donner une contrainte supplémentaire : la
direction de projection. En géométrie plane, cette
direction de projection est une droite. En géométrie
dans l'espace, cette direction est un plan.
Le choix le plus simple - et physiquement le plus fécond -
est de prendre la direction perpendiculaire à D. Mais tout
autre choix de direction, autre que parallèle à D,
serait aussi un choix mathématiquement valide.
Ceci est indispensable à la physique, pour définir
les produits intérieur et extérieur, entre vecteurs.
Par exemple, en électricité, en représentation
de Fresnel d'une tension et d'un courant alternatifs, quand on
multiplie la tension par la projection intérieure de
l'intensité, on obtient la puissance active.
Quand on multiplie la tension par la projection extérieure
de l'intensité, on obtient la puissance réactive.
Avec un plan P et un vecteur, on définit de la même
façon, la projection intérieure sur ce plan :
 ,
et la projection extérieure au plan :
,
et la projection extérieure au plan :
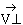 ,
qui est orthogonale à tout vecteur de P.
,
qui est orthogonale à tout vecteur de P.
Une troisième projection :
"dioptrique", ou "anti-intérieure".
La projection "dioptrique" régit la projection de
la longueur d'onde sur le plan du dioptre. Nous la rencontrons en
faisant la construction de Snell-Huyghens, pour les lois de
réflexion-réfraction de Snell et Descartes. C'est la
quantité lambda1 . sin i1 =
lambda2 . sin i2 qui se conserve : une
longueur de phase le long du plan du dioptre. Et corrélativement,
la vitesse de phase le long du plan dioptrique. Il serait intéressant
de revisiter la terminologie employée par Fresnel et Hamilton
: ils ont certainement dénommé cette projection
particulière.
L'inverse du vecteur longueur d'onde, ou covecteur nombre d'ondes
par unité de longueur, se projette intérieurement sur
le plan du dioptre. D'où le baptême suggéré
de projection anti-intérieure pour la longueur d'onde sur le
plan dioptrique.
Quatrième projection :
anti-extérieure.
Elle est utile pour la loi de Biot et Savart, qui donne le champ
magnétique créé par un circuit parcouru par un
courant électrique.
5
.
Suite
Dans le prochain article, nous verrons les autres conséquences
de notre définition : variance des composantes, changements de
base, invariance du module envers les changements de base, produit
intérieur et produit intérieur contracté
(produit scalaire). Ensuite, nous verrons le produit extérieur
et les tourneurs. Puis nous verrons en détail la métrique
et le calcul sur tourneurs et vecteurs, et leurs applications en
cristallographie. Enfin nous verrons les liens entre dimension
physique, et caractère tensoriel, puis les simplifications
apportées à l'enseignement de l'électromagnétisme.
Auteur : Jacques Lavau
[1] connue pourtant depuis le 17e siècle, par
Marin Mersenne (1588 - 1648), qui l'a utilisée avec succès.
[2] A. Einstein; Eine neue
formale Deutung der Maxwellschen Feldgleichungen der Elektrodynamik.
Prüss. Akad. Sitz. 1916. pp 184-188. Ce terme "Sechstervektor"
a été propagandé (voire inventé ?) par Arnold Sommerfeld.
[3] Sir E. Whittaker; A
History of the Theory of Aether & Electricity. Dover Pub. New
York. 1989. 1ère éd. 1951.
[4] Physiquement, un espace n'est euclidien - où
la parallèle à une droite par un point existe, et est unique - que si
on ne regarde pas trop loin, pas trop gros, ni trop petit. Un objet
technique tel qu'un tour, une fraiseuse, une grue, s'inscrivent sans
difficulté dans un espace euclidien. Il est impossible de réaliser à la
surface de la Terre un objet matériel de plus de 20 km de dimension,
qui incarne encore l'idéal euclidien : la courbure de la Terre, et les
fléchissements des matériaux, dictent une loi plus dure que notre
géométrie simplificatrice. On peut trouver des "objets" de lumière qui
aient cette taille, voire plus grands, mais on ne les trouve que dans
le vide, donc loin de la Terre, sinon les mouvements de l'air dévient
la lumière; c'est pourquoi les étoiles scintillent à nos yeux. Et il
faut les placer loin d'une masse importante comme le Soleil, ou autre
étoile: les masses courbent la lumière dans leur voisinage... Les
notions de droite et de parallèle nous claquent alors à la figure. Mais
il nous reste le pouvoir de décider d'un espace idéal
euclidien, local, tangent à l'espace réel.
Et si on regarde petit, alors on s'aperçoit que notre notion de
point, qui nous semble si évidente, nous claque aussi à la figure :
physiquement, le point n'existe pas. Il est impossible d'assigner à des
électrons d'être là, en un point. Leur espace symplectique propre (de
dimension au moins 6) se projette dans un certain volume diffus, qui ne
peut ni être arbitrairement réduit, ni être totalement défini. Beaucoup
des mystères de la chimie, par exemple la stabilité de la
molécule de benzène, découlent de cette impossibilité d'assigner une
position précise à un électron, ni à aucun autre quanton (objet
quantique).
[5] Le théorème de Thalès, permet, par des reports
parallèles, de mesurer où l'on veut, à partir de où l'on
sait.
[6] La démonstration exige la continuité de
l'application "multiplication par un scalaire". Aucun contre-exemple ne
concerne la physique, qui a bien d'autres problèmes avec l'adéquation
des nombres "réels" à ses besoins.
[7] En algèbre, on appelle corps un ensemble doté
de deux lois de composition internes, et qui est un groupe
commutatif pour la première. Privé de l'élément neutre de la
première loi, il est aussi un groupe pour la seconde loi, qui de plus
est distributive sur la première loi.
Un groupe est un ensemble sur lequel on a défini une loi de
composition interne associative, présentant un élément neutre, et dont
tout élément possède un inverse.