Ils ont
mathématisé
de travers
1 .
Multiplier deux segments, en CM2 et en sixième.
2 .
La multiplication des vecteurs.
2.1.
En première et terminale.
2.2.
En terminale-DEUG-prépa-BTS et similaires.
2.3.
En fin de maîtrise, et en troisième cycle.
2.4.
Résumé : un praxéogramme disloqué.
2.5.
En mécanique quantique.
3 .
La pratique usuelle mise au pied du mur.
4 .
Pourtant, il existe une méthode physique.
5 .
Encore plus simple.
6.
« Well, Papa ! Can you
multiply triplets ? »
7 .
Et si ça n'est pas vecteur, alors c'est quoi ?
8 .
Conclusion.
Ils
ont mathématisé de travers
Auteur : Jacques Lavau.
La malchance de mathématiser de travers
est une mésaventure très banale, que tout chercheur
actif connaît plusieurs fois dans sa carrière. Ce qui
n'est plus anodin du tout, c'est que 151 ans après, on n'ait
pas encore corrigé quelques bévues d'un grand
ancêtre (Hamilton), qui règnent encore sur
l'enseignement de la physique. Nous donnons cette correction en
détail, répartie sur six articles. Il est étonnant
qu'aucun mathématicien n'eût encore songé à
expliquer aux physiciens ces choses élémentaires, à
un niveau élémentaire.
1 . Multiplier
deux segments, en CM2 et en sixième.
Si le lecteur
accepte de se souvenir du modeste début de ses brillantes
études, il devrait se souvenir qu'à l'aide de figures
de ce genre, son instituteur lui a appris qu'on obtient la surface
d'un rectangle, en multipliant la longueur d'un côté par
la longueur d'un côté adjacent.
|
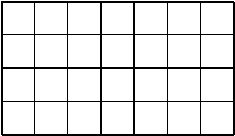
|
Commençant
par travailler sur des entiers et des longueurs entières, vous
avez été invités à constater que
"multiplier" un segment de longueur 4 par un segment perpendiculaire de
longueur 7, dans la même unité, produit bien une
surface rectangulaire, d'aire 28 carreaux carrés. Chaque
carreau unitaire ayant l'unité de longueur pour
côté.
|
L'énoncé restait très
prudent et rigoureux : "multiplier le nombre qui mesure la
longueur par le nombre qui mesure... etc.", évitant
d'introduire des ambiguïtés entre {segment : ensemble de
points} et {longueur : grandeur} (en dimension 1), et entre {surface
: ensemble de points} et {aire : grandeur} (en dimension 2).
Peu d'années après, vous avez
appris à ramener le calcul de l'aire d'un parallélogramme
à celle d'un rectangle. Par une opération qu'on
omettait de désigner[1],
on obtenait la hauteur du parallélogramme; sur cette hauteur
et la base, on construisait un rectangle, puis on multipliait la
mesure de la base par la mesure de la hauteur, et on obtenait la
mesure de l'aire du rectangle; et par le jeu de deux triangles
égaux,
on montrait que cette mesure était aussi celle de l'aire du
parallélogramme.
|
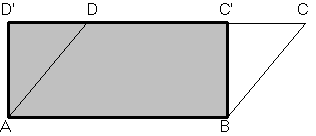
|
Les
triangles BCC' et ADD' sont égaux. Le rectangle ABC'D' a
même aire que le parallélogramme ABCD.
Pourvus
de procédures sur les mesures des aires, on n'avait pas
explicité de moyen d'appréhender ces grandeurs
indépendamment d'une unité de mesure.
|
2 . La
multiplication des vecteurs.
2.1. En
première et terminale.
Vous avez pratiqué le produit
cartésien,
y compris le produit R x R associé au plan. Vous
avez caractérisé les translations, obtenant ainsi des
vecteurs. Vous aviez en mains tous les composants, prêts à
servir. La progression logique eût été que le
prochain pas fût d'enchaîner sur le produit
extérieur
des vecteurs, obtenant ainsi l'aire orientée du
parallélogramme. Mais personne n'a pratiqué la
progression logique.
2.2. En
terminale-DEUG-prépa-BTS et similaires.
A partir de la terminale, vous avez appris deux
produits, un "produit scalaire" et un "produit
vectoriel". Conformément à l'infirmité
de l'école anglaise de Hamilton (1805-1865) et de Cayley
(1821-1895), qui ne parvenait pas à bien discerner un vecteur
d'une liste de nombres (pouvant être éventuellement des
composantes de vecteur) sans structure ni règle, ces produits
vous ont été enseignés comme des résultats
de calculs sur "composantes",
c'est à dire en réalité sur coordonnées, au
lieu d'une définition
intrinsèque, dont on eût vérifié la
cohérence mathématique (notamment
géométrique).
Cela donnait quelque chose du genre : pour obtenir le "produit
scalaire" vous additionnez les produits de "composantes" (c'est à dire
en réalité "coordonnées") deux
à deux [2].
Pour le "produit vectoriel", c'est un vecteur
dont on obtient les "composantes"
(c'est à dire en réalité "coordonnées") par
telle différence de
produits croisés. Les repères étant tacitement
toujours orthonormés.
A ce
stade-là,
le praxéogramme[3]
des concepts emmagasinés dans votre cursus scolaire, a
l'allure suivante :
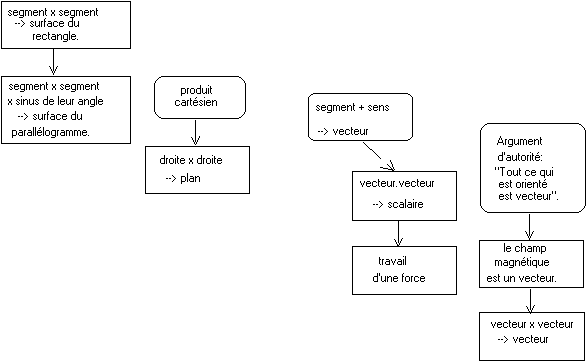
|
|
Notamment,
on vous a fait apprendre (donc approuver) des affirmations de ce genre :
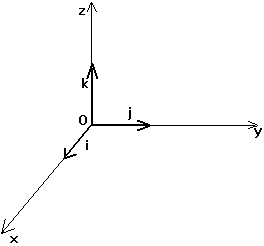
«Le
vecteur unitaire k est le produit vectoriel du vecteur i par
le vecteur j, unitaires.»
Or
comme chacun de ces vecteurs est de dimension unitaire, soit
physiquement un mètre, le vecteur k est en même
temps de longueur un mètre carré.
Ce
qui est une propriété fort surprenante pour un vecteur
unitaire dans un repère orthonormé : 1 m = 1 m². Et
tout ce qui s'ensuit : 1 m = 1 m2 = 1 m3 = 1 m-1,
etc.
Et
comme, implicitement, un vecteur ne serait qu'une liste de
(trois) nombres, et que 1 m = 100cm, alors 100 = 10 000 = 1 000
000 = 0,01, etc.
|
Et vous êtes encore loin d'avoir vu toutes
les autres contradictions... Evidemment, vous n'y aviez vu que du
feu, alors. Ainsi va la physique de concours, avec son ultimatum
habituel : approuvez à l'instant, ou partez.
Aujourd'hui, quitte à faire un effort
d'honnêté, vous devriez vous souvenir de votre
stupéfaction, la première fois que vous avez vu le
professeur sortir de sa manche la mystérieuse troisième
direction, dans laquelle il a mystérieusement choisi un sens
pour y placer son mystérieux troisième vecteur.
Rappelez-vous : vous n'avez commencé à y "croire"
un peu, que lorsqu'on vous a donné l'exemple d'applications en
magnétisme. Comme par hasard : il est impossible de voir
un champ magnétique, alors qu'on peut voir tourner une
vitesse angulaire et un moment cinétique. Aussi fallait-il
commencer par vous mettre sous dépendance en magnétisme,
avant de vous asséner le produit vectoriel en mécanique,
toute vigilance anesthésiée.
Les professeurs de mathématiques, qui
réticents, enseignaient quand même cette absurdité,
parce qu'elle est au programme, faisaient passivement
confiance : "il paraît que ça sert en physique",
et renonçaient à comprendre pourquoi[4].
Sans se douter qu'il n'y avait rien à comprendre, et tout
à
refaire.
2.3. En fin de
maîtrise, et en troisième cycle.
Si vous avez appris l'algèbre
extérieure
et l'algèbre tensorielle, notamment pour survoler les
leçons
sur la Relativité, vous avez repris la progression logique
commencée à l'école primaire, là où
on vous avait forcé à la discontinuer et
délaisser.
De nouveau, on vous a autorisé à distinguer un nombre
d'une grandeur.
|
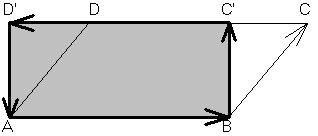
|
Le
rectangle ABC'D' a même aire orientée que le
parallélogramme ABCD.
"Orientation"
signifie ici sens de parcours du périmètre : parcourir
d'abord le segment AB, puis le segment BC.
Cette
aire orientée est l'opposée de celle du
parallélogramme ADCB.
|
Mais trop souvent, au lieu de vous donner les
heures de travaux dirigés nécessaires pour
maîtriser
le calcul extérieur, et ses applications physiques, le
professeur a biffé tout son travail, d'une contradiction :
«ceci signifie le produit vectoriel»[5].
Conclusion pragmatique de cette contradiction : oublier la
cohérence
logique, oublier l'algèbre extérieure, garder le
"produit vectoriel", qu'emploie la puissante
majorité. Vous n'avez guère gardé en
mémoire
que la règle de changement de base. En oubliant de s'en servir
pour vérifications de cohérence. En oubliant comment se
servir en pratique des règles de covariance et de
contravariance.
2.4.
Résumé
: un praxéogramme disloqué.
On remarque un
domaine cohérent à gauche, mais écartelé
par de longues années d'inaction dans le cursus scolaire :
l'algèbre linéaire est totalement cohérente avec
la géométrie.
Séparé et incompatible, un domaine
purement autoritaire à droite, autour du "produit
vectoriel", qui domine le gros des physiciens et des
électrotechniciens. Un domaine intermédiaire
(semi-correct) entre les deux, où le produit scalaire
hésite à être intérieur ou scalaire, et
où
scalaire est tacitement non-défini.
Les mauvaises relations entre métiers ont
fait que personne ne s'est soucié de restituer une
cohérence
décente dans les systèmes de concepts enseignés
de ci de là. Sauf H. Weyl, E. Cartan et A. Einstein; nous y
reviendrons.
2.5. En
mécanique quantique.
Un vecteur d'état dans un espace
de Hilbert de dimension infinie, n'a plus rien à voir avec un
véhicule, ni avec rien de géométrique ni de
vectoriel. Plus besoin de cohérence géométrique,
semble-t-il. Et un sentiment d'autarcie totale envers le restant du
monde, et envers les critères de cohérence et de
rigueur élaborés ailleurs : le moment magnétique
et le spin redeviennent des vecteurs. Enfin bref, des listes
de nombres.
Préférant, pour la facilité
des calculs, un système d'unités sans unités
(abstrait : il ne peut y mesurer) où la vitesse de la
lumière
vaut 1, la constante h
vaut aussi 1, la charge de l'électron vaut -1, le physicien
quantique perd la pratique de la discipline de la covariance, ne
ressent plus le besoin de distinguer un nombre d'une grandeur, et
n'utilise plus qu'à moitié les vérifications
apportées par l'équation aux dimensions. Ainsi
mutilé,
il ne voit plus aucune objection au règne du produit
vectoriel sur la physique de concours. Il est aussi dispensé
de distinguer les grandeurs extensives des grandeurs intensives, car
il ne rencontre plus guère les premières. Le niveau
d'énergie d'un électron lié à un atome,
quotient d'une extensive par un nombre de particules, est grandeur
intensive : énergie pour UN électron.
3 . La
pratique usuelle mise au pied du mur.
Ayant coupé les ponts d'avec la
cohérence
mathématique, et d'avec la réalité
géométrique
et physique sensible, ce "produit vectoriel" oblige
à cascader les astuces mnémotechniques, pour obtenir le
moindre renseignement. Exemples : le sens du courant induit dans une
dynamo, le sens dans lequel tourne un moteur, le sens du courant au
secondaire d'un transformateur. Il faut de longues années de
dressage, pour obtenir un rendement significativement supérieur
à celui de pile-ou-face. La physique n'en sort pas grandie...
|
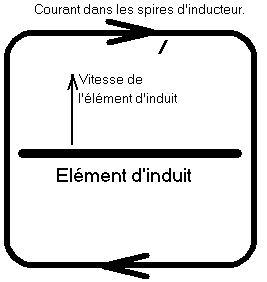
Prenons
le cas d'un brin conducteur d'induit, se déplaçant devant
une pièce polaire d'inducteur. On sait dessiner le sens du
courant dans les spires d'inducteur.
Le
schéma est entièrement dans le plan de la spire,
parallèle au plan déterminé par la vitesse du brin
d'induit passant devant la pièce polaire, et par le brin
conducteur lui-même.
On
veut prévoir le sens de la f.é.m. dans l'induit.
Prenez
votre chronomètre et faites vos jeux : le + est à droite, ou
à gauche ?
|
|
Quelle durée vous a-t-il fallu pour
être
certain(e) de la réponse exacte ? Dix secondes auraient dû
suffire. Il était superflu de s'inquiéter si le brin
d'induit est derrière un pôle "nord" ou devant
un pôle "sud", ou entouré par un solénoïde,
et de s'encombrer d'une troisième dimension sans pertinence.
Superflu aussi, d'introduire deux fois un tire-bouchon, un bonhomme,
ou divers doigts dans une machine à courant continu.
|
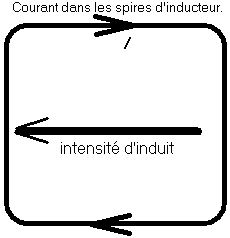
Prenons
un cas encore plus simple : sachant le sens du courant dans
l'élément d'induit d'un moteur à courant continu,
prévoir le sens de rotation.
Cinq
secondes suffisent.
|
|
4 . Pourtant,
il existe une méthode physique.
Votre établissement ne dispose sans doute
pas du matériel d'expérience : à 10 000F, c'est
inabordable pour la plupart des lycées. Pourtant, plusieurs
des manuels que vos élèves peuvent acheter, en exhibent
la manipulation : l'ampoule d'hydrogène raréfié,
dans lequel on injecte un faisceau d'électrons, que l'on peut
dévier, avec un champ magnétique et/ou un champ
électrique. Vous constatez dans quel sens tourne votre
faisceau d'électrons : dans le sens où tourne le
courant dans la bobine.
|

|
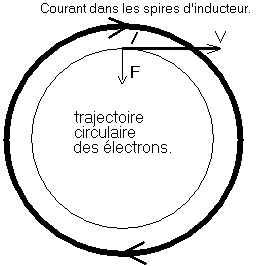
On
n'a porté ici que le résultat expérimental.
Mais
pourquoi avoir caché l'intermédiaire théorique :
le champ magnétique ?
|
C'est que, depuis longtemps, j'ai abandonné
avec joie la représentation du champ magnétique par un
bâton muni d'une pointe de flèche, sachant combien cette
représentation est vicieuse, hors-sujet.
Maxwell, Weber, Thomson, Curie, Weyl, Feynman
nous ont révélé que le champ magnétique
est "un truc-qui-tourne". En 1827, Ampère nous a dit
pourquoi[6].
Il est vrai que son hypothèse des courants
moléculaires
heurtait le préjugé anti-atomiste de l'époque,
et que les électrons n'ont été inventés
qu'entre 1891 et 1897.
Mais bien peu de collègues ont eu la
chance de bénéficier d'enseignants suffisamment
cultivés pour dessiner ces trucs-qui-tournent, comme
des bâtons, avec une flèche de rotation autour. Or cette
représentation est bien moins incorrecte : le sens de
rotation étant enfin correct, le bâton reste hors-sujet,
et n'a aucun des comportements dimensionnels adéquats.
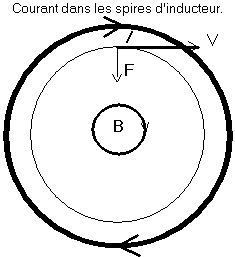
Je dessinerai donc le champ magnétique,
et ceux des êtres de rotation qui sont mathématiquement
comparables (moment cinétique par exemple) de manière
physiquement correcte : c'est dans un plan, et ça tourne
dans ce plan. Ajoutons donc le champ magnétique à
notre schéma. Le schéma reste plan.
|
|
Nous
obtenons donc, de la spire au champ, et du champ à la
trajectoire, toujours un rond dans un rond, et qui tournent pareil.
|
|
Et
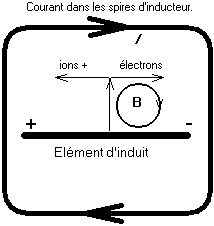
pour l'appliquer à notre dynamo ?
Très
simple, il suffit de dessiner comment les électrons sont
déviés, toujours dans le sens du champ (ici à
droite de la figure), et les ions métalliques positifs (du
réseau cristallin de cuivre ou d'aluminium) en sens inverse (
ici à gauche de la figure), donc notre élément
d'induit se comporte comme un générateur dont le
pôle + est
à gauche de la figure.
|
|
|
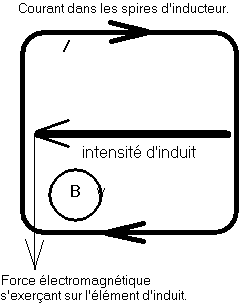
Cas
encore plus simple : sachant le sens du courant dans
l'élément d'induit d'un moteur à courant continu,
prévoir le sens de rotation.
Il
suffit de se rappeler que notre faisceau d'électrons, dans
l'expérience du faisceau d'électrons dans un gaz
raréfié, circule en sens inverse du courant conventionnel
: les électrons sont négatifs.
Le
champ dévie la course des électrons selon son sens de
rotation. Autrement dit, il dévie le courant en sens inverse. Ce
qui nous donne le sens du quart-de-tour à opérer sur le
courant, pour obtenir la force.
En
prime, nous obtenons que la force électromotrice qui s'exerce
sur l'induit, dès qu'il tourne en moteur, est bien CONTRE
l'intensité qui le fait tourner, est donc bien
contre-électromotrice.
|
|
Ainsi, il nous a toujours suffi d'une règle
physique pour obtenir le sens d'une action physique, force
électromotrice, ou déviation d'une trajectoire. On n'a
aucun besoin de se référencer au bonhomme, à
l'agent de police sur une place à sens giratoire, ni aux
tire-bouchons, ni à dieu-sait-quels doigts de dieu-sait-quelle
main. L'électromagnétisme n'a pas à s'encombrer
de l'anatomie des primates homo sapiens et autres. Seule la
physique des neutrinos et de l'interaction faible, est contrainte
à
traiter d'hélicités droite ou gauche.
5 . Encore
plus simple.
|
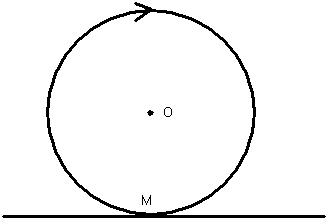
Considérons
une roue, roulant sans glisser. Considérons le champ des
vitesses en tout point de ce disque solide, dans un repère
lié à la route. Prenez un crayon et un bout de papier
Le
schéma vous donne toutes les indications nécessaires pour
dessiner le sens du rotationnel de ce champ de vitesses (c'est
ici la même chose que la vitesse angulaire du solide).
Vous
avez 5 secondes.
|
|
Bien. Posez les crayons. Le point de contact M,
et le centre du cercle O étaient superflus pour votre
réponse.
Il ne nous importe pas non plus, que le schéma plan,
représente une vue en élévation d'un solide
tridimensionnel, ou que la scène se déroule à
Flatland, pays imaginaire de dimension 2, où un disque roule
sur une droite. Mathématiquement, dimension 2, 3, 4, 5, ou 77,
cela ne fait aucune différence sur le rotationnel. La seule
exigence est que la dimension soit au moins 2.
|
En
deux secondes vous pouviez donner une réponse exacte, et bien
suffisante :
|
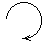
|
|
En
cinq secondes, vous pouviez dessiner encore plus :
|

|
Hélas, on peut parier que vous vous
êtes
encombré de complications hors sujet, qui vous ont
gaspillé
un temps énorme. On peut gager que vous êtes allé
chercher une troisième dimension, hors-sujet (mais puisqu'on
vous l'a apprise...) pour y poser un "vecteur", qui
n'a plus rien à voir avec un sens de rotation. Puis, en
contemplant vos doigts, vous vous êtes longuement demandé
si ce "vecteur" montait à travers la feuille
de papier, ou descendait à travers elle. Peut-être vous
êtes vous questionné sur le point d'origine exact d'un
tel "vecteur", ou sur son "axe".
Certains sont peut-être même allés jusqu'à
tout redessiner en perspective...
Tout ce tintouin, pour PERDRE le sens de
rotation, et gagner à la place une information qui n'a
aucune chance de jamais devenir pertinente.
Or, ce sens de rotation, était
déjà
dessiné, il vous suffisait de LE GARDER.
6.
« Well, Papa ! Can you multiply triplets ? »
[7]
Tout ce fatras, ces complications hors-sujet,
découlent d'une petite tragédie qui a commencé
en 1843 : Hamilton emmêla deux cahiers des charges
incompatibles, quand il créa l'algèbre des quaternions,
en voulant créer les quotients des vecteurs de E3.
Son cahier des charges sémantique, aurait dû n'aboutir
qu'à l'algèbre tensorielle. Mais il s'est donné
un cahier des charges structurel calqué sur les nombres
complexes, autrement dit sur le complexifié de la droite
réelle R, avec ce produit interne, dont
l'interprétation géométrique plane emmêle
les rotations dans les translations. Et Hamilton a oublié
complètement l'indispensable algèbre des unités
physiques. Puis il a appliqué naïvement ses
hypercomplexes à l'espace physique réel (qu'il voyait
en minkowskien avant la lettre). Les physiciens, dans leur
majorité,
ne se sont pas encore aperçus que cette confusion entre
rotations et translations, où l'on fourre tout dans le
même
sac, tourne le dos à tout sens physique.
Un an plus tard, en 1844, Grassmann (1809-1877)
publia l'outil mathématique approprié, avec notamment
la première distinction ferme entre nombres et grandeurs
(même
si les grandeurs restent provisoirement abstraites, avant toute
application physique). Mais voilà, Grassmann était un
professeur peu connu, et son style philosophique kantien (aussi
terrifiant que celui des Eléments d'Euclide)
contrevenait aux habitudes des mathématiciens de
l'époque,
alors que Hamilton était un astronome déjà connu
pour génial, ex-enfant prodige. Son formalisme canonique de la
mécanique, de 1834, est toujours insurpassé. Hamilton a
connu l'Ausdehnungslehre de Grassmann[8]
vers 1852, mais ne s'est guère préoccupé à
son sujet que de calembours (mangeur d'herbe), et des
questions d'antériorité.
Depuis ces dates, les physiciens jouent de
malchance, et, sous couleur de simplifier (couleur qui leur
sert à esquiver leurs tâches de clarification
sémantique), ratent tous leurs rendez-vous avec leurs outils
mathématiques corrects et appropriés[9],
se contentant d'adorner d'habits neufs les vieilles confusions. Dans
son traité de 1873, J. Clerk Maxwell (1831-1879) multiplie les
mises en gardes contre les impropriétés de sa
mathématisation[10],
ne s'y fiant qu'à demi. Les mots "vector product"
ne se rencontrent que sous la plume de Clifford (1845-1879), en
1877[11].
Tous deux ignoraient l'oeuvre de Grassmann jusqu'en 1878[12].
Visiblement, en 1894, les mises en garde de Clerk Maxwell
étaient
déjà oubliées[13],
car Pierre Curie (1859-1906) prit soin de redémontrer en
détail combien la représentation du champ
magnétique
par un vecteur, est impropre[14].
Peine perdue que celle de Curie : les physiciens perdirent de vue le
modèle physique correct (dû à Ampère
(1775-1836), Clerk Maxwell, W. Thomson (1824-1907), W. E. Weber
(1804-1891), Pierre et Jacques Curie), parce que la
mathématisation
usuelle le contredisait. Et aussi parce qu'ils se débattaient
alors dans une ignorance physique dont nous n'avons plus la moindre
idée : l'électron n'a été inventé
qu'entre 1891 et 1897, et prouvé en 1897; avant cela, Faraday
(1791-1867), Clerk Maxwell, Poynting (1852-1914), Heaviside
(1850-1925), etc. ont dû héroïquement bricoler des
concepts inextricables pour imaginer la simple conduction
électrique
(et la charge électrique) : ici une vibration d'éther,
là un vortex, ou une discontinuité des
vecteurs déplacements, un croisement de vortex, une
éponge de vortex, une contraction des tubes de
forces, etc...
On peut constater au long des publications et
manuels du siècle écoulé, que la faute de
mathématisation, a éliminé le modèle
physique correct (les courants ampériens), et consacré
la conception erronée d'rsted (1777-1851), de Wollaston
(1766-1828), de Faraday, etc. ("spectre de limaille
facile implique vrai vecteur magnétique",
voire "courant électrique invisible implique vortex").
Même Dirac (1902-1984) s'y est laissé prendre jusque
vers 1970 [15].
Chaque fois que voir une grandeur physique
orientée
fut impossible, des physiciens furent déroutés, et
beaucoup se sont égarés. Le prestige d'une
mathématisation obscure a souvent suffi à éteindre
leur perception kinésique. Nos élèves, eux,
préfèrent dédaigner toute la physique, pour sa
malmathématique embrouillée.
7 . Et si
ça
n'est pas vecteur, alors c'est quoi ?
Une minorité de lecteurs bâille
d'ennui : elle sait déjà que le champ magnétique,
le flux magnétique, le moment cinétique, le moment
d'une force, la vitesse angulaire, l'accélération
angulaire, la vitesse aréolaire, et quelques autres grandeurs,
de symétrie similaire, sont des tenseurs antisymétriques
de rang deux.
Des quoi ? grommelle la majorité,
au bord de l'insurrection. Elle n'a pas tout à fait tort.
Donnons donc un synonyme bref et clair; qualifions-les de
tourneurs gyreurs.
Oui, le mot historiquement choisi était déjà pris, et
utilisé dans les ateliers. "Gyreur" était tombé en désuétude et oublié, il vaut donc un mot neuf, grâce à Jean-Louis Leroy-Bury.
Le mot "vecteur" aussi
était déjà très pris, depuis plus de 40
siècles, avant d'être repris en 1837 par Hamilton,
à
usage mathématique. Le moustique est le vecteur de la
fièvre
jaune et du paludisme. Au 18e siècle, les colporteurs furent
les vecteurs des pamphlets révolutionnaires. Certaines
fusées
sont des vecteurs nucléaires. Dans le dictionnaire de latin,
on trouve une famille de 21 termes autour du verbe "vehere"
et du nom "vector" (au sens de chariot, puis
d'animal bâté ou de trait, de cavalier, puis de passager
d'un navire), et encore 4 autour de "convehere", 4
avec "per__", 4 avec "circum__", 10
avec "de__", 2 avec "re__", 5 avec
"trans__", 5 avec "e__", 7 avec
"ad__", 1 avec "a__", 6 avec
"sub__", 2 avec "super__". En
français, nous avons gardé aussi "véhicule",
"véhiculer", "convection", "convecteur",
"évection" [16].
La famille décuple, si l'on considère que "vea"
et "veha" sont les anciennes formes de "via"
(voie, route), et que "vexare" (secouer, puis
tourmenter) est l'intensif de "vehere";
en français, nous en avons gardé : "voie",
"convoi", "convoyer", "dévoyer",
"dévier", "viabiliser", "viaduc",
"voyer", "voirie", "voyage",
"viatique", "vexer", "convexe",
"vétérinaire" (de "veterina"
: bêtes de somme), etc. La racine indo-européenne est
connue : VAH, et désignait le transport sur un
char[17].
L'extension aux autres moyens de transports est venue ensuite[18].
Gardons donc à "vecteur"
un usage spécifique, pour les grandeurs physiques qui
véhiculent, qui translatent, telles que le déplacement,
la vitesse, l'accélération, l'impulsion, la force, le
champ électrique, le potentiel-vecteur, etc. Le gradient de
concentration d'une espèce chimique sera mieux qualifié
de "covecteur".
Hamilton s'exprimait par ces
égalités
: "vehend + vector = vectum, et
vectum - vehend = vector",
additionnant ainsi un point et un vecteur, alors
qu'en notation opératorielle, on écrirait de nos jours
plutôt :
vector(vehend) = vectum.
"Gyreur" désigne
désormais les grandeurs physiques qui prennent un vecteur
d'une espèce, le projettent dans un plan stable, et lui font
faire un quart de tour dans ce plan stable, pour engendrer un certain
autre vecteur. Nous consacrerons un chapitre entier aux gyreurs.
L'opérateur de projection est appelé
"projecteur" par les mathématiciens depuis
longtemps. Ce mot est connu des physiciens quantiques.
L'opérateur
de rotation n'a pas encore reçu de baptême bref qui
fasse l'unanimité. "Rotateur" est utilisé en
anatomie, et en chimie organique (lumière polarisée),
et je suggère de le réutiliser. Le gyreur est le
composé d'un projecteur orthogonal sur un plan, et d'un
rotateur d'un quart de tour dans le même plan stable.
Nous verrons au chapitre algébrique, que l'ordre de la
composition est indifférent : ces deux opérateurs
commutent entre eux (propriété peu banale).
La minorité citée plus haut
proteste à son tour : «On n'a pas besoin de gyreurs,
on disait déjà "vecteur axial"»
(variante : "pseudovecteur"[19]).
"Vecteur", disiez-vous ? C'est pourquoi vos
collègues comprenaient toujours vecteur, tout court. La nuance
"pseudo", ou "axial"[20],
était invariablement perdue et incomprise par vos
contemporains moins instruits. D'ailleurs, même chez ceux qui
la prononçaient, la nuance "axiale" restait
lettre morte dès qu'ils calculaient, car eux aussi se
servaient d'un "produit vectoriel", dont ils
devaient ensuite corriger à la main les fautes de
symétries.
Voilà pourquoi l'auteur considère les nuances "pseudo"
et "axial" comme disqualifiées. Aucune nuance
ne peut racheter le "produit vectoriel". Aucune
habitude ancrée ne peut racheter le fait qu'on se trompe de
mathématisation depuis 1843. Nos grands ancêtres
avaient des excuses, nous pas; et les meilleurs d'entre eux nous
avaient prévenus de leurs doutes.
Nos gyreurs, ont déjà
été
baptisés "bivecteurs" par Grassmann. Le terme n'a
pas eu grand succès, ni sa généralisation en
multivecteurs, ou en p-vecteurs. Je devine deux raisons à cet
insuccès : leur obscurité, et la collision avec les
"quadrivecteurs" relativistes, utilisés dans
l'espace de Minkowski. Ces "quadrivecteurs"
ronflants restent fort mal nommés; il ne s'agit que de
vecteurs fort ordinaires, dans un espace de dimension quatre.
L'obscurité reste un défaut grave : comment feront les
gens simples, pour deviner que "bivecteur" veut dire
"être-de-rotation", tels une vitesse angulaire, un
champ magnétique, ou une surface orientée en rotation ?
"Bi-vecteur" ne se rapporte à aucun verbe d'action.
Or le verbe d'action est indispensable aux gens simples.[21]
8 .
Conclusion.
Cet article introductif se bornait à vous
motiver. Dans les prochains articles, nous donnerons les
définitions,
tant pratiques que mathématiques et physiques, des termes
nouveaux, et de ceux qu'on croyait si sûrs, et qui furent si
mystificateurs si longtemps.
Nous différencierons, et grapherons, les
deux systèmes d'axiomes, l'un fort, l'autre faible, dans
l'ambiguïté desquels on a trop joué à
cache-cache jusqu'à présent. Le système
d'axiomes forts des vecteurs, système géométrique,
est celui que vous employez dès que vous dessinez des
vecteurs, et est celui qui convient à toute la physique
classique macroscopique. Le système faible, minimaliste,
purement algébrique, des espaces vectoriels
généraux,
était du reste, lui aussi violé par les usages
relâchés
des physiciens.
Nous rappellerons les propriétés
algébriques et géométriques des vrais vecteurs,
notamment leurs symétries. Nous donnerons toutes les
propriétés des gyreurs. Nous donnerons les moyens
d'en visualiser la connectique : des lois physiques relient les
grandeurs entre elles, et dictent des restrictions irréfragables.
Nous dégagerons les liens fiables entre
la dimension physique et le type géométrique d'une
grandeur physique. Par des tableaux de correspondance, nous en
dégagerons la syntaxe. La syntaxe
géométrique-tensorielle
des lois physiques, est un garde-fou tout aussi indispensable que
l'équation aux dimensions.
Nous donnerons en détail toute la
pratique algébrique des gyreurs, en relation avec les autres
grandeurs géométriques de la physique, notamment les
vecteurs. Un exercice en bases non orthonormées sera
détaillé.
Nous résumerons l'histoire de la
genèse
de la faute de mathématisation. Cela ne nous donnera que les
causes contingentes. Pour publier les causes structurelles, beaucoup
de prérequis manquent encore, notamment les prérequis
éthiques. Ces causes structurelles sont toujours actives, et
chacun manque encore du recul nécessaire. Le
contrôle-qualité
est à 100% dans les mains du producteur, qui l'étrangle.
Enfin, si nous regorgeons en persiflages, nous n'avons aucune
théorie
fiable du fonctionnement du théoricien; ni dans le cas du
théoricien indépendant, ni dans celui du
théoricien
dépendant de sa position en cour. Alors que les nombreux
exemples fournis par l'Histoire incitent à la défiance.
Auteur : Jacques Lavau.
[1] Nous
détaillerons cette projection orthogonale extérieure.
C'est indispensable.
[2] Il est indispensable que nous
détaillons ultérieurement la projection orthogonale
intérieure et le produit intérieur.
[3] Praxéogramme : graphe
des actions, composant en séquence une action plus complexe.
Exemple : une recette.
[4] Exception méritoire :
Jean Barbotte; Le calcul tensoriel. Bordas, 1948. Paris.
Barbotte mentionne le livre de L.
Brillouin, mais n'imite pas ses renoncements diplomatiques.
[5] Un exemple parmi tant d'autres
: A. Dahan-Dalmedico & J. Peiffer; Une histoire des
mathématiques. Routes et dédales. Page 286, 4e ligne,
édition de poche Points, Seuil. 1986 Paris.
[6] André-Marie
Ampère. Théorie mathématique des
phénomènes électrodynamiques uniquement
déduite de l'expérience. Gauthier-Villars. Paris
1827.
[7] William
Rowan Hamilton; Mathematical Papers. Cambridge Univ. Press. Lectures
on Quaternions. Dublin
1953.
[8] Hermann
Günther Grassmann; Die Lineale Ausdehnungslehre. 1ère
édition en 1844, édition refondue en 1862. Traduction
française par D. Flament : La science de la grandeur
extensive. Lib. A. Blanchard. 1994 PARIS.
[9] Ratant par exemple
Barré de Saint-Venant (1797-1886) : "Mémoire sur les
sommes et différences géométriques et sur leur
usage pour simplifier la Mécanique", note à
l'Académie des Sciences, septembre 1845.
[10] James
Clerk Maxwell. A Treatise on Electricity and Magnetism.
Réed. Dover, New York, 1954.
[11] William
Kingdon Clifford; Notes of lectures on quaternions.
Mathematical Papers. Chelsea, New York 1968.
[12] Clifford a publié en
1878 ses Applications of Grassmann's extensive Algebra, venant
juste de découvrir l'Ausdehnungslehre.
[13] Dans son Matter and Motion,
de 1877, Maxwell avait déjà oublié ses
réserves, et présentait une règle chirale pour
représenter un moment cinétique. Matter
and Motion. Réed. Dover. New York 1991.
[14] Pierre Curie : Sur la
symétrie des phénomènes physiques. Journal de
Physique, 3e série, t. III, PARIS 1894.
[15] En 1975, P. A. M. Dirac a
désavoué sa précédente croyance en des
monopôles magnétiques, à la déception de
Price, qui croyait en avoir observé un. cf Paul Perrier; Le
premier monopôle magnétique ? La Recherche
n° 61, pp. 965 - 966. Paris 1975.
[16] en astronomie : se dit d'une
inégalité des mouvements de la lune, liée au
déplacement du périgée et aux variations de
l'excentricité.
[17] Jean Varenne; Grammaire
du sanskrit. QSJ-PUF, Paris 1979. Il semble qu'on trouve des
descendants en russe : vodit'/viesti : conduire; voz :
chariot; voznitsa : cocher; vojd'/voditel' : conducteur.
[18] Emile Benveniste; Le
vocabulaire des institutions indo-européennes. T1. Editions
de Minuit. Paris 1975.
[19] Plus caustique, Michel Hulin
écrivait : "vecteur de mauvaise foi". B.U.P.
n°572. PARIS, 1975
[20] Attention aux choix des mots
! Ces grandeurs "axiales" n'ont justement pas d'axe, mais un
plan stable.
[21] J. W. Gibbs avait proposé le terme de
dyadic, qui n'a pas percolé jusqu'aux physiciens de langue
française.














