Voici la preuve que tout triangle est équilatéral !
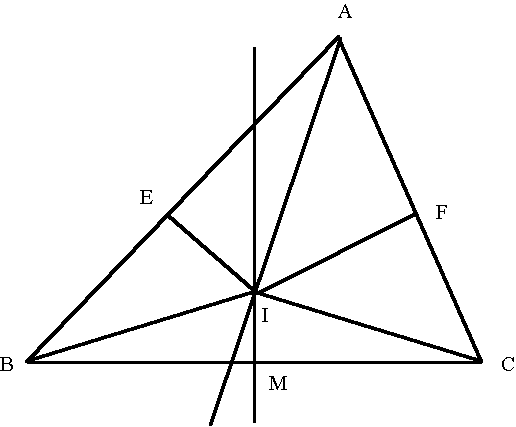
Vous tracez un triangle quelconque ABC.
Vous tracez la bissectrice intérieure en A, et en M la médiatrice du segment BC.
Elles se coupent au point I. Le triangle IBC est donc isocèle, et les angles (non orientés)
IBC et ICB sont égaux. Les segments IB et IC sont égaux.
De I vous abaissez en E et F les perpendiculaires aux droites AB et AC.
Rappel : cas d’égalité des triangles rectangles (isométrie en langage plus moderne).
Deux triangles rectangles qui ont l’hypoténuse égale et un côté de l’angle droit égal sont isométriques.
C’est le cas des triangles EIB et FIC.
Ils ont hypoténuses égales : IB = IC (car IM est médiatrice de BC).
Et EI = IF (car AI est bissectrice de l’angle intérieur en A).
Donc les angles (non orientés) EBI et FCI sont égaux.
Donc les angles non orientés ABC et ACB sont égaux, car ABC = ABI + IBC et ACB = ACI + ICB.
Donc le triangle ABC est isocèle en A.
Il suffit de recommencer sur l’une quelconque des deux orientations restantes pour prouver qu’il est équilatéral.
Notre démonstration est générale : tout triangle quelconque est équilatéral.
Qui trouve l’erreur ?
Cet exemple est caractéristique de très nombreuses fautes de raisonnement généralement admises comme correctes.
Ce qui est marrant, c’est d’appliquer le même truc à un problème de géométrie euclidienne élémentaire.