Un contraste demeure étonnant : de nombreuses parties de
l'enseignement des mathématiques sont bien faites. Mais
là je me suis attaqué à un domaine où
pratiquement tout demeure fort mal fait. Comment peut s'expliquer un
tel contraste dans l'état des mathématiques ? Par exemple
la théorie des probabilités est bien faite. Seulement
voilà : la totalité du travail pouvait être
achevé dans un seul corps de métier. Alors qu'ici, nous
sommes dans la mathématisation de la physique, ce qui sollicite
l'interface entre plusieurs corps de métier, donc un niveau de
discipline relationnelle et interprofessionnelle qui reste inconnu et
impensable entre mathématiciens et physiciens.
Nous sommes finalement peu nombreux à vivre à la jonction
de plusieurs métiers, et à marier plusieurs cultures.
Voilà pourquoi l'auteur fut au bout du compte le seul à
pouvoir écrire cet article, qui tâche de rattraper 151 ans
de retard au temps où il fut écrit, et 161 ans de retard
maintenant (en 2005).
Le diffuseur des Editions de la Maison des Sciences de l'Homme a
gravement manqué la diffusion du livre Le nombre, une hydre
à n visages ; entre nombres complexes et vecteurs, ce qui
justifie que j'aie mis en ligne ici le dernier article du livre, les 41
pages qui sont écrites par moi-même.
"Vecteurs" ? 151 ans de déloyaux services.
1. Le confusionnisme et la mystification étaient évitables.
2. Quatre à six mille ans de présence dans la langue :
3. Les certitudes dès la première ressemblance venue.
4. La confusion entre nombres et grandeurs.
4.1. Les prolégomènes oubliés.
4.2. Premier progrès en cercle vicieux : des espaces vectoriels de dimension 1 ?
4.3. La granularité nulle de R n'est pas pertinente en physique.
4.4. Les lois physiques sont dans QUOI, au juste ?
4.5. L'acte fondateur de la physique, qui la distingue des mathématiques, est heuristique.
4.6. Problèmes de pédagogie quotidienne.
4.7. Solutions en pédagogie quotidienne.
Autre exemple : le lien entre le monôme dimensionnel et le caractère géométrique tensoriel.
4.8. Conséquences dans la stratégie de management des concepts.
5.1. Rappel : interprétation géométrique des nombres complexes.
5.1.1. Addition des nombres complexes : interprétation.
5.1.2. La multiplication des nombres complexes ?.
5.1.3. Ces deux interprétations sont fascinantes, mais contradictoires...
5.1.4. Image complexe du produit scalaire.
5.2. “Well, Papa! Can you multiply triplets ?” (Hamilton 1853).
6.3. Le produit "vectoriel" : fausse solution à un vrai besoin.
7.1. Inventaire : quatre ou cinq usages. Ou huit ?
7.1.1. Les usages à délimitation immédiatement correcte.
7.1.2. Les usages confus, à démêler.
7.1.3. Synthèse de l'inventaire des significations de tous les "vecteurs" prétendus.
7.3. Garde-fous abstraits, garde-fous concrets, garde-fous sociaux.
8. Un tourneur, ça n'est pas vecteur du tout, même "pour simplifier".
8.1. Multiplier deux segments, en CM2 et en sixième.
8.2. La multiplication des vecteurs, en première et terminale.
8.3. La multiplication des vecteurs, en terminale-DEUG-prépa-BTS et similaires.
8.4. En fin de maîtrise, et en troisième cycle.
8.5. Résumé : un praxéogramme disloqué.
8.6. Et si ça n'est pas vecteur, alors c'est quoi ?
9. Conclusion : le sixième travail d'Hercule ?
La malchance de mathématiser de travers est une mésaventure très banale, que tout chercheur actif connaît plusieurs fois dans sa carrière. Ce qui n'est plus anodin du tout, c'est que 151 ans après[1], on n'ait pas encore corrigé quelques bévues d'un grand ancêtre (Hamilton), qui règnent encore sur l'enseignement de la physique. Il est étonnant qu'aucun mathématicien n'eût encore songé à expliquer aux physiciens ces choses élémentaires, à un niveau élémentaire.
La physique est la principale consommatrice de ce qu'on appelle les vecteurs. Elle est l'une des principales consommatrices des analogies géométriques des nombres complexes, et des hypercomplexes. Je vais montrer que ce vocable de "vecteur" est grevé d'une vaste polysémie pleine d'ambiguïtés et de confusions. On peut exhiber de nombreux manuels qui changent subrepticement de définitions, ou contredisent leurs définitions, jusqu'aussi souvent que toutes les trois pages.
Je montrerai que les distinctions fondamentales ne sont toujours pas faites, et les axiomatiques de base, pas encore mises au net. Je rappellerai qu'en physique, une large part de l'axiomatique nécessaire, est par nature inachevable, notamment l'axiomatique des grandeurs physiques. Ce n'est nullement une raison valide pour se croiser les bras, car chacun a besoin d'utiliser tous les jours, depuis le CE2 et le CM1, ces grandeurs physiques dont l'axiomatique est par nature, inachevée, et à remanier encore plusieurs fois dans l'avenir de l'humanité.
J'en conclurai par un transfert de principes depuis l'informatique, vers la physique. En effet, là seulement on a commencé d'élaborer des principes de développement et de management, pour tenir compte de ce que tout programme écrit, sera relu et transformé plusieurs fois par d'autres programmeurs. On n'a pas encore architecturé les systèmes de concepts de la physique, en tenant compte de cet impératif élémentaire : faciliter les remaniements, et les corrections des malfaçons. Les manuels sont tous écrits comme si leurs auteurs jouissaient de cette présomption de sécurité qui s'exprime par les trois adages : "actuel = correct", "Il n'y a pas lieu de séparer la description du fait physique, de son modèle mathématique, car nous sommes certains d'être infaillibles dans l'usage de ces mathématiques que nous méprisons[2]", et "Après moi, il n'y aura plus d'autres prophètes". Il suffit d'essayer, pour voir que séparer la description physique, du modèle de calcul, autorise une stabilité salutaire de la physique, et rend la description indépendante des erreurs de mathématisation, et de ses corrections successives. Et surtout, cela oblige enfin à élaborer une mathématisation sur la base d'un cahier des charges, enfin explicite. Le reste est alors facile, pour les cas que nous étudierons.
Nous proposerons ultérieurement des solutions pour donner une sécurité, une stabilité, et une ergonomie aux systèmes de concepts et de modèles de la physique, dont on s'est fort peu soucié jusqu'à présent, et dont on a grand besoin pour élaborer une stratégie didactique qui tienne la route, pour l'enseignement de la physique. Parti d'erreurs de mathématisations déjà bien connues à l'époque de nos études, voici trente ans, et toujours pas corrigées depuis, nous avons peu à peu découvert de grandes carences en méthodologie générale.
Le mot "vecteur" était déjà très pris, depuis plus de 40 siècles, avant d'être repris en 1837 par Hamilton, à usage mathématique. Le moustique est le vecteur de la fièvre jaune et du paludisme. Au 18e siècle, les colporteurs furent les vecteurs des pamphlets révolutionnaires. Certaines fusées sont des vecteurs nucléaires. On envisage d'utiliser un virus comme vecteur du gène dont les myopathes manquent. Cet article vous est venu sous les yeux grâce au vecteur "Le nombre : une hydre à n visages. Entre nombres complexes et vecteurs".
Dans le dictionnaire de latin, on trouve une famille de 21 termes autour du verbe "vehere" et du nom "vector" (au sens de chariot, puis d'animal bâté ou de trait, de cavalier, puis de passager d'un navire), et encore 4 autour de "convehere", 4 avec "per__", 4 avec "circum__", 10 avec "de__", 2 avec "re__", 5 avec "trans__", 5 avec "e__", 7 avec "ad__", 1 avec "a__", 6 avec "sub__", 2 avec "super__", 8 avec "in__", 2 avec "dis__", 1 avec "prae__", 5 avec "pro__". En français, nous avons gardé aussi "véhicule", "véhiculer", "convection", "convecteur", "évection" [3], "invective". La famille décuple, si l'on considère que "vea" et "veha" sont les anciennes formes de "via" (voie, route), et que "vexare" (secouer, puis tourmenter) est l'intensif de "vehere"; en français, nous en avons gardé : "voie", "envoi", "convoi", "convoyer", "dévoyer", "dévier", "viabiliser", "viaduc", "voyer", "voirie", "voyage", "viatique", "vexer", "convexe", "vétérinaire" (de "veterina" : bêtes de somme), etc. La racine indo-européenne est connue : VAH, et désignait le transport sur un char (Varenne 1979). L'extension aux autres moyens de transports est venue ensuite (Benveniste 1975). Le H désigne là non pas un vague souffle à la française, mais bien une gutturale, à la façon du g néerlandais, éventuellement susceptible de mouillure, à la façon du g danois. Par le germanique, nous en avons aussi hérité "wagon", "vaguemestre", "tramway", "thalweg". Le "veg" de Norvège (chemin du Nord), et celui du prénom féminin "Solveig" (chemin du Soleil) en descendent aussi directement. On trouve aussi des descendants en russe : vodit'/viesti : conduire; voz : chariot; voznitsa : cocher; vojd'/voditiel' : conducteur. Or le char comme engin de guerre et de transport, est attesté dès les deux premières invasions kourganes, pré-indo-européennes, vers 4400 et 4200 A.C., tandis que l'archéologie linguistique rigoureuse bute sur la date de dislocation et d'émiettement de l'indo-européen, vers 2200 A. C.
Pour restituer de la précision et de la stabilité à notre langue scientifique, et aux concepts plus ou moins conscients qu'elle génère dans les têtes de nos élèves, je préconise de garder à "vecteur" un usage spécifique, pour les grandeurs physiques qui véhiculent, qui translatent, telles que le déplacement, la vitesse, l'accélération, l'impulsion, la force, le champ électrique, le potentiel-vecteur magnétique, etc. Le gradient de concentration d'une espèce chimique sera mieux qualifié de "covecteur".
Hamilton s'exprimait par ces égalités : "vehend + vector = vectum, et
vectum - vehend = vector",
additionnant ainsi un point et un vecteur, alors qu'en notation opératorielle, on écrirait de nos jours plutôt :
vector(vehend) = vectum.
Nous allons dans la suite de l'article résoudre les autres termes de la polysémie confuse, dont chacun peut remarquer les ravages dans son environnement de travail.
A chaque fois, je prendrai soin de ne dériver le substantif que d'un verbe d'action compréhensible par le grand public technicien. Le verbe d'action, évoquant une action qu'ils ont pratiqué, et qu'ils peuvent pratiquer avec leurs muscles, est indispensable aux gens du peuple. Et à quoi sert la science, si elle se barricade, par le biais d'une obscurité artificielle, contre la compréhension du grand public, dont les impôts paient nos salaires et nos instruments ?
Les Frères Jacques ont chanté "La voix du sang" : Tous les 18 à 20 ans, un homme retrouvait la grande émotion de sa vie, sous la forme d'une charmante jeune fille rencontrée dans la rue. Et à chaque fois il se ruait sur elle en s'exclamant (je cite de mémoire) :
"La voix du
sang !
j'te reconnais !
T'es mon enfant !
La voix du sang
!
La voix du sang ! "
Enthousiasmé, il avait aussitôt une brève liaison, apparemment incestueuse. Le dernier couplet conclut :
"la voix du
sang
s'tait foutu d'dans
régulièr'ment".
Parmi les exemples historiques de gens qui s'enflamment de certitude à la première ressemblance venue, les cas de Caspar Wessel, de Jean Robert Argand, et de William R. Hamilton, sont parmi ceux qui évoquent le plus fâcheusement La voix du sang. On pourrait continuer la chanson :
"Trois
composantes !
j'te reconnais !
T'es un vecteur !
L'instinct
physique !
L'instinct physique!"
Exemples non isolés, hélas. Avec
méchanceté,
mais hélas trop de ressemblance, on pourrait caricaturer que
pour le physicien de base, "vecteur", ça
veut dire trois : trois composantes, qu'ils confondent
d'ailleurs avec coordonnées. Et réciproquement : trois,
ça veut dire vecteur. A l'appui de ma caricature, voici
deux exemples, exhibant comment ils ont réagi dès qu'on
a dépassé trois composantes :
- Depuis Minkowski,
les physiciens relativistes se gargarisent d'un ronflant
"quadrivecteur", pour désigner tout vecteur
fort ordinaire, mais sur un espace de dimension quatre.
- En
1916, sous l'influence d'A. Sommerfeld, même A. Einstein se
croyait obligé de baptiser de "Sechster-vektor",
ce dont il donnait entre parenthèses la traduction en clair :
tenseur antisymétrique de rang deux (sur un espace de
dimension quatre). Il n'a mis sa terminologie au net que vers 1921,
sans doute grâce à Hermann Weyl. Tandis qu'un E.
Whittaker (1951) est resté jusqu'à sa mort au stade du
"Six-vector" hétérogène.
Le développement des mathématiques et de la physique a usé et abusé de la précipitation définitive vers la première ressemblance venue. Aussi Bolzano, puis les autres mathématiciens du mouvement rigoriste, furent-ils d'abord accueillis comme des chiens dans un jeu de quilles : ils dérangeaient la joie de comprendre, ou de croire comprendre à peu de frais. Et ils furent accueillis comme un cas de divorce par les physiciens.
De nos jours encore, trop de mathématiciens stoppent l'analyse au premier isomorphisme venu, et dédaignent ostensiblement de s'intéresser aux différences, à leurs structures, et à leurs significations : "We will show that all (fill the blank) look alike". La phrase magique "Et on est ramené à un problème connu!" emporte leur sang-froid. Ils sont convaincus qu'être mathématicien, vaut une dispense d'enquêter sur la sémantique, et sur tout ce qui différentie les objets de pensée qu'il vient de mettre en isomorphisme. Tout chercheur chevronné sait que l'ennui de se cramponner à la première analogie venue, est qu'aussitôt, on néglige de produire toutes les autres analogies. Et en matière d'idées, la productivité conditionne la qualité; on ne peut choisir en sécurité que parmi beaucoup d'idées, et lorsqu'elles sont presque toutes ensemble dans la tête.
Cette confusion parasite le coeur des mathématiques depuis les auteurs grecs; elle s'est adaptée chez les auteurs arabes; elle a continué à parasiter tout au long du 19e siècle (sauf Grassmann, et partiellement Maxwell), et elle continue encore d'obscurcir l'apprentissage des sciences. Elle n'est qu'un cas particulier de l'oubli total d'une systématique des niveaux d'abstraction. Elle a induit la confusion entre coordonnées, et composantes de vecteur.[4]
Bien qu'on définisse les espaces vectoriels abstraits assez tard dans les études, au début des études supérieures, nos bambins manipulent dès l'école primaire, souvent dès le CE2, des membres d'espaces vectoriels de dimension 1 : les grandeurs concrètes, et les grandeurs physiques (autres que vectorielles, ni tensorielles). Puis, l'enseignement secondaire étant disloqué entre spécialités étrangères les unes aux autres, nos potaches oublient tout, aux mains de matheux purs, qui n'entendent rien à la physique. Ils s'installent alors durablement dans la confusion entre nombres et grandeurs, entre le tout-abstrait, et le demi-abstrait.
Les nombres sont tout-abstraits. Le nombre "quatre" n'est pas "quatre ânes", ni "quatre cailloux", mais ce qui est commun entre eux, par la relation "on peut établir une bijection entre ces deux collections", respectivement d'ânes et de cailloux. C'est donc une classe d'équivalence : la relation est symétrique, réflexive, transitive.
Les grandeurs physiques sont semi-abstraites, et gardent une propriété du monde réel, dont les nombres sont dispensés : une signification, une unité-étalon, et la grammaire de variance qui y est associée.
Les grandeurs physiques sont dispensées des propriétés fort compliquées des mesures, et des résultats de mesures (avec toutes leurs sortes d'incertitudes et d'erreurs), et de celles du stockage de ce résultat sur un papier ou dans une machine électronique, avec ses problèmes de largeur et de résolution limitées.
Pour les grandeurs concrètes et les grandeurs physiques, l'égalité a un sens, si l'on sait définir un protocole de comparaison et de mesure. Par exemple, comparer deux longueurs, comparer deux aires, ou comparer deux lots de paquets de lessive, sous fardelages différents. A ce prix, nous avons le droit d'écrire une égalité de grandeurs, même en unités inhomogènes, comme : 1 tour = 2p radians.
La grandeur physique est définie comme l'abstraction commune à ce qui dans la réalité est justifiable de la même famille de protocoles de mesure, dont la précision et le coût peuvent être très différents, mais qui ont tous pour objet de comparer une même sorte de grandeur. Par exemple une longueur, ou une masse au repos.
C'est donc aussi une classe d'équivalence. Elle est bien moins abstraite qu'un nombre, car elle est un descripteur de quelque chose. Elle est tenue à la syntaxe inhérente à la vocation sémantique de chaque grandeur physique.
Nous allons avoir besoin de caractériser ces grandeurs pratiques et concrètes d'une part (par exemple 500 flacons d'un médicament), et ces grandeurs physiques d'autre part, par leur lien avec une grandeur unité, et avec l'ensemble des nombres réels. Nous allons donc définir les grandeurs scalables. Nous aurons aussi besoin de distinguer entre les grandeurs arbitrairement scalables, et les grandeurs nombrables, pour lesquelles existe une unité absolue définie par la nature, et non par une société humaine.
En 1873, Clerk Maxwell consacrait le premier paragraphe de son Treatise (Clerk Maxwell 1873) à expliquer que toutes les grandeurs physiques sont le produit d'un nombre par un échantillon de cette grandeur, appelé unité. Pourtant, encore aujourd'hui, légions sont ceux qui répugnent à s'apercevoir que dans tout problème physique ou pratique de la géométrie, les grandeurs qu'on considère, ne sont que rarement des nombres, mais des produits de nombres par des unités physiques. Ouvrez n'importe quel ouvrage de mathématicien consacré aux mathématiques de la physique; vous constaterez qu'il vous affirme sans rire, que les fonctions de la physique sont à valeur dans R, ou dans C, ou dans Rn, ou dans Cn.
Prenons la largeur de cette feuille de papier, qui sort de mon imprimante. Elle mesure 21 cm; ou 210 mm; ou 0,21 m. Or, il n'existe aucune fonction réelle ayant la propriété que : 21 = 210 = 0,21.
Tandis qu'il est parfaitement correct d'écrire que : 21 cm = 210 mm = 0,21m.
Ces deux égalités ne sont pas écrites entre nombres, mais entre grandeurs physiques. Elle dénotent des classes d'équivalences déterminées par les principes des mesures. Ici, seuls les principes d'au moins un protocole de mesure des longueurs, au moins un principe de construction des appareils de mesure, et des campagnes de mesures vérifiant l'équivalence et la bonne adéquation de ces appareils et de ces protocoles, peuvent justifier la définition de la grandeur physique, et les conditions de l'égalité.
Tout le drame historique et social, est que les sept phrases banales, écrites ci-dessus, semblent avoir été trop matérialistes pour échapper au mépris et à la phobie des mathématiciens, et trop mathématiciennes, pour échapper au mépris de l'abstraction de trop de physiciens. Chacun clôturant prématurément son métier longtemps avant que le partenaire indispensable n'ose ou ne daigne ouvrir le sien; chacun laissant en friche une large part de son métier de base.
Le premier progrès est de remarquer que si cette feuille de papier pèse autant que 5 g, ou que 50 dg, alors cette grandeur masse présente les propriétés d'un élément d'un espace vectoriel de dimension 1. La coordonnée naturelle est contravariante à l'unité de masse, prise comme "vecteur" de base. Du point de vue de l'algébriste, la question semble close.
Du point de vue du didacticien, ce premier progrès se mord la queue. Nos élèves doivent rencontrer cette question de la variance des grandeurs physiques relativement aux unités, plusieurs années avant d'aborder les espaces vectoriels en algèbre : dès le CM1, dès qu'on traduit de centimètres en mètres. De plus, le choix des mots est traditionnellement désastreux. On a accoutumé tout notre corps enseignant de physiciens à considérer que les vecteurs sont de dimension 2, ou 3, mais jamais 1, tandis que les mathématiciens sont accoutumés à identifier comme synonymes "vecteur" avec "membre d'un espace vectoriel abstrait".
Sur de telles bases, le résultat sera consternant, si on leur assène désormais que la masse, la température, la surface et le volume, dont aucun n'est vectoriel, sont néanmoins des espaces vectoriels. Nous proposerons plus loin une solution à cette fâcheuse polysémie autour de vecteur-espace-vectoriel.
Nous n'avons encore ni jeu d'axiomes, ni terminologie simple - à usage grand public, j'insiste, c'est indispensable - pour les espaces des grandeurs physiques, a commencer par ceux qui sont de dimension 1. Nous n'avons pas non plus de stratégie didactique stable. Notre système d'enseignement bafoue trop souvent et la sécurité, et l'ergonomie, dans les concepts incohérents qu'il impose à nos enfants.
Très peu de grandeurs physiques véritables ont la granularité nulle de R. La charge électrique est toujours multiple entier relatif de la charge élémentaire. L'action est toujours multiple entier de h. Ce sont des exemples de granularité finie totalement définie : des grandeurs nombrables, qui n'ont aucun degré de liberté. Plus nombreux encore sont les exemples de granularité finie floue, pour les grandeurs arbitrairement scalables.
Les nombres de R sont définis comme de largeur infinie, sauf une proportion négligeable d'entre eux, tels que les entiers et les fractionnaires. Or une vie humaine ne nous donne jamais le temps d'écrire un nombre de largeur infinie. Aucun instrument de mesure ne nous donne de mesure dont la précision et la définition soient de largeur infinie. Exceptés en principe les quantiques e (charge de l'électron) ou h, bases de grandeurs nombrables, aucune grandeur physique n'est définie avec une précision infinie. Aucun calculateur ne peut ni stocker, ni calculer de nombres de largeur infinie. Ils sont plus couramment limités à 64 ou à 80 bits, rarement 120 bits. Il existe bien quelques logiciels de calculs, à largeur de nombres qui n'est limitée que par la mémoire totale de la machine, mais il faut en payer le prix, en temps de calcul comme en puissance machine.
Or l'ensemble des entiers relatifs Z, n'est pas un corps mais un anneau. Sur un anneau, on ne construit pas des vrais espaces vectoriels, mais des modules. Cette distorsion est toujours renvoyée dans le non-dit de la physique. Intellectuellement, c'est un travail de mathématicien, mais les mathématiciens s'en moquent. Et un physicien qui s'en occuperait, se verrait couper les crédits. No man's land en friche.
Sur le plan topologique, on s'est enthousiasmé pour l'analyse Non Standard de Robinson. Or, si elle est féconde pour fournir une topologie moins coûteuse, avec de bien pratiques voisinages, notamment voisinage de l'infini, elle non plus n'atteint pas encore la cible des besoins de la physique. En fait, elle n'a pas encore été prévue pour traiter de la limitation de la granularité.
Cette hypnose sur la granularité nulle de R a entraîné la physique dans des impasses toujours renouvelées. Notamment, du temps d'Einstein et de Bohr, cela a engendré le monstre de la dualité onde-corpuscule. Nos grands ancêtres étaient tellement inhibés à imaginer des règles numériques et syntaxique à granularité finie, qu'ils se sont crus obligés - E. Schrödinger excepté, et oublié - de les justifier par des corpuscules néo-newtoniens. Bonjour les dégâts!
Dans des modules. Ces modules forment entre eux des produits cartésiens, rarement des produits tensoriels, parfois des algèbres extérieures. Or, depuis 150 ans les physiciens sont les premiers résistants à la notion même d'algèbre tensorielle, ou extérieure. Ils ont continué en autarcie à radoter des produits "vectoriels" : produits internes à valeur vectorielle. Le travail des pionniers, comme Mersenne en physicien, puis Grassmann en géomètre, n'a guère été poursuivi. Personne n'a formalisé jusqu'au bout l'algèbre des unités et grandeurs physiques. Cela ne fait que l'objet d'introductions ou d'annexes dans les manuels (pas tous... les meilleurs seulement). Sans intégration suffisamment profonde avec les corps des mêmes manuels.
Et quelle est la raison profonde pour laquelle le produit extérieur d'une grandeur à valeur dans l'espace des vecteurs de l'espace géométrique affine des positions, par une grandeur dans l'espace des impulsions, donne une grandeur dans l'espace des moments angulaires ? Quel est le lien conceptuel nécessaire entre ces espaces physiques, indépendamment du fait que nous nous en servons pour y constater des lois ? Nous serons des physiciens dignes de notre époque, quand nous aurons été capables de donner un cadre conceptuel à ces réalités que nous ne savons que constater pour l'instant, et que nous manipulons à tâtons. Il est certain que le cadre tensoriel est indispensable, et devrait enfin balayer des archaïsmes injustifiables. Nous allons voir qu'il ne suffit pas entièrement, et qu'il faut le compléter. Nous aurons à nous demander si cette complétude est un objectif entièrement réalisable.
C'est d'abord un aveu d'ignorance, et un aveu d'existence. J'avoue qu'il existe quelque chose dans le monde réel, qui échappe et résiste au libre arbitre de mon imagination, et dont je ne sais pas tout. C'est très différent du théorème d'incomplétude de Gödel. Cela signifie que nous n'avons aucune chance d'écrire dans notre vie le système d'axiomes complet et définitif d'un quelconque des espaces de grandeurs physiques, alors qu'il est certain que nous aurons toute notre vie l'usage urgent desdits espaces de grandeurs physiques. Qu'au contraire, notre système d'énoncés, doit intégrer la certitude que notre travail devra être profondément révisé et remanié par d'autres personnes. Et que cela ne serve pas d'excuse pour continuer à ne rien faire, à ne rien formaliser!
L'aveu d'ignorance et d'existence a été formulé par Bunge (1973). Il visait à l'époque le folklore néopositiviste qui encombre la mécanique quantique, et utilisait cet aveu d'ignorance pour fonder l'attitude réaliste critique. Si je projette de mesurer le niveau d'énergie d'un électron, j'avoue ne pas en connaître tout d'avance, et surtout j'avoue croire à l'existence de quelque chose à mesurer : cet électron, et ce niveau de d'énergie. Si ma mesure créait l'électron et son niveau d'énergie, on peut se demander comment l'univers a bien pu exister avant que les physiciens quantiques le mesurent, et comment leurs ancêtres ont pu exister et procréer...
Bunge est un des auteurs les plus honnis par les physiciens - mais aucun n'avoue pourquoi. Sans doute parce que Bunge a raison plus souvent qu'à son tour.
Il semble trop souvent que le but de l'enseignement soit d'empêcher nos élèves de vérifier la signification des symboles et des formules qu'ils ont tant de mal à assimiler (socialement, l'obscurité est sélective) :
On leur interdit les identificateurs clairs; puisque les vrais mathématiciens qui font de vrais longs calculs ont l'usage d'identificateurs raccourcis à une seule lettre, ils n'imaginent rien d'autre au monde, et veulent imposer ça à des élèves, dont beaucoup n'ont encore jamais maîtrisé un long calcul, de leur vie :
"Longueur d'onde" = "célérité" ´ "période" est officiellement interdit... Seul est autorisé : l = v ´ T.
La solution est évidente à un instituteur avisé, qui faisait écrire (avant l'ère de la T.V.A.) :
bénéfice = prix de vente - prix de revient;
On leur impose de lire et d'écrire des lignes inhomogènes dimensionnellement, où tous les coefficients sont entassés, sans aucun aide-mémoire physique, suivies, mais seulement à la dernière ligne du calcul, d'une unité physique parachutée - et qui est vraie ou fausse, par pur hasard.
On a sous-estimé l'insécurité due à la manie d'interdire aux élèves de porter les unités physiques à l'intérieur des formules de physique, les privant ainsi de pouvoir vérifier la cohérence dimensionnelle de leur écriture. On leur interdit de laisser l'unité à côté de son coefficient, dans l'application numérique des formules physiques.
Prenons un cas très simple, le calcul d'une longueur d'onde à partir de la célérité et de la période.
l = 343 m/s ´ 0,025 s, si simple, que théoriquement, les élèves ne devraient pas s'embrouiller avec la forme hélas réglementaire (et contradictoire) :
l = 343 ´ 0,025
l = 8,6 m.
Contradictoire, disais-je. Cette longueur d'onde est une grandeur physique, mais dans les lignes intermédiaires, on l'a traitée comme un nombre, produit de nombres. En pratique, ils s'embrouillent, nos élèves, et tout n'est de leur seule faute. C'est la doctrine officielle qui marche sur la tête. Les ouvrages des séries de Bringuier, chez Hachette - donc, comme tous les concurrents, sous aval d'inspecteurs de l'enseignement -, sont particulièrement riches en exemples de ce Jean-foutrisme :
v(5) = -1,74 ´ 5 + 20,83 puis : v(5) = 12,1 m.s-1 = 43,7 km.h-1. Fin de citation, p16, Bac Pro T2.
La solution est d'expliciter le schéma d'héritage de nombre vers grandeur, et de restructurer nos progressions pédagogiques autour de cet héritage. Avec leurs oeillères de purs matheux, nos professeurs du secondaire font oublier aux élèves ce que les instituteurs leur avaient appris, et que la vie autour d'eux confirme : peu des nombres qu'ils manipulent et calculent représentent vraiment des nombres, mais ont bien vocation à représenter des grandeurs physiques, ou pratiques. Or un nombre qui représente des mètres de tranchée, un qui représente des palettes de lessive, un qui représente un taux d'intérêt composé, et un qui représente la vitesse moyenne d'un mobile, n'ont pas du tout la même vocation à être bombardés n'importe où dans une formule. On peut additionner toutes sortes de nombres. Mais on ne peut additionner des pots de fleurs avec des mètres de tranchées. On peut multiplier toutes sortes de nombres. Mais multiplier une vitesse par une fréquence, ça ne donnera sûrement pas une longueur d'onde.
S'il s'en était souvenu, Elie Cartan aurait sûrement réfléchi à deux fois avant d'écrire des barbarismes dimensionnels tels que "Toute matrice carrée de degré 2n est décomposable en une somme d'un scalaire, d'un vecteur, d'un bivecteur, etc... et d'un n-vecteur." (Cartan 1937). Car les classes des vecteurs, bivecteurs, multivecteurs, tous tenseurs, sont à dériver de la classe des grandeurs scalaires (ils héritent de la variance envers les unités), et non de la superclasse des nombres complexifiés.
Cinq règles à retenir, à titre d'axiomes provisoires :
On ne peut additionner (ou retrancher) que des grandeurs de même nature.
On peut multiplier une grandeur physique nombrable par n'importe quel nombre entier. On peut multiplier une grandeur physique arbitrairement scalable par n'importe quel nombre réel.
Dans la famille des grandeurs physiques, écrire une égalité, suppose qu'on a réussi à définir une méthode expérimentale, et des instruments, pour comparer.
On a alors le droit d'écrire une égalité entre grandeurs, comme 210 mm = 21 cm. Nous exprimons la grandeur physique comme le produit d'un nombre, par une unité de cette grandeur. Il faut avoir défini ou construit un étalon de cette grandeur-unité.
Toute grandeur physique a un inverse, et il n'est pas nécessaire de définir à nouveau une méthode de mesure. Exemples : un décamètre est gradué à 100 divisions par mètre. L'inverse du mètre s'écrit m-1.
On est libres de multiplier une grandeur physique par n'importe quelle autre grandeur physique; ou de diviser par une grandeur physique non nulle. Cette opération est externe : elle génère une autre grandeur physique distincte.
Savoir si le résultat a un intérêt pratique, n'est que la question suivante. On peut montrer que les résultats réellement pratiques forment une structure assez simple et remarquable.
Toutes les conversions d'unités coulent alors de source. On s'impose de n'écrire que des égalités vraies en grandeurs physiques. Par exemple, pour traduire une masse volumique (ici celle d'un acier) donnée dans des unités non S.I., vers le Système International, on commence par écrire la tautologie :
7,8 .
![]() =
7,8 .
=
7,8 .
![]() Jusqu'ici, on n'a certainement violé ni la physique, ni la
mathématique.
Jusqu'ici, on n'a certainement violé ni la physique, ni la
mathématique.
Puis on multiplie le second membre par une fraction égale à 1. On la choisit de façon à faire apparaître les éléments d'unités voulus, et faire disparaître, par simplification, les éléments d'unités indésirables. Ici on veut faire disparaître grammes du numérateur, et y faire apparaître kilogrammes, faire disparaître cm3 du dénominateur, y faire apparaître m3. Procédons en deux étapes :
7,8 .
![]() =
7,8 .
=
7,8 .
![]() ´
´
![]() ´
´
![]() =
7,8.
=
7,8.
![]() (commutativité
nombre.unité)
(commutativité
nombre.unité)
7,8.
![]() =
7,8.
=
7,8.
![]() ´
´
![]() =
7800 kg/m3.
=
7800 kg/m3.
Aux élèves doués, la méthode peut paraître lourde, peu valorisante, et socialement peu sélective. Ils préfèrent deviner le bon résultat, au flair. Mais tous les autres élèves préfèrent ma méthode : elle est incassable!
Ceci déborde le cadre du présent article, et fait l'objet d'une autre publication.
Les conséquences stratégiques et managériales, il faut aller les chercher ailleurs, là où elles sont déjà connues, dans une branche d'activité à cycles de vie des concepts, bien plus courts qu'en physique. En science de l'économie d'entreprises, la "drosophile" est l'industrie pharmaceutique. Ici, je suggère l'industrie informatique comme drosophile. Elle peut convenir, dans la mesure où elle est assez bien supervisée par des universitaires très dynamiques, en plus d'avoir été fortement secouée par des entrepreneurs très dynamiques. L'emploi du passé semble hélas se justifier en 1995, où l'avenir étouffe sous un quasi-monopole.
Cela signifie qu'il faut architecturer nos systèmes de concepts, en se centrant sur la nécessité des remaniements de maintenance, soit pour remédier aux malfaçons, soit pour répondre à de nouveaux besoins, comme tenir compte des nouvelles découvertes, ou tenir compte des nouveaux utilisateurs, de cultures bien différentes de celle des pionniers.
A l'heure actuelle de nombreux manuels (surtout dans le technique, et je pense en particulier à la série des Niard, chez Nathan) sont en passe de devenir inutilisables, et bons à jeter si les réformes que je préconise aboutissent, car leurs auteurs n'ont jamais pensé à donner une représentation des phénomènes physiques, qui soit stable envers le remaniement des concepts pseudo-mathématiques auxquels ils ont cru bon d'identifier la physique. Les remaniements étant l'avenir normal et le plus probable, il faut prévoir l'architecture avec le maximum de stabilité, tant globale que locale, malgré tous ces prochains remaniements et corrections. On n'a encore jamais étudié la didactique dans cette perspective des remaniements inévitables, par correction de l'exposé incorrect. On s'est contenté d'envisager la correction des erreurs de l'élève tout seul, qui sont censées ne jamais se propager au niveau professeur, ni n'en provenir. C'est un peu court.
D'un point de vue pratique, il nous reste à désigner par un baptême convenable ces espaces des grandeurs physiques, qui ne sont nullement ceux qu'on emprunte aux mathématiciens. Je suggère au lecteur de devenir acteur à ce sujet, et de faire lui-même ses propositions. Pour fédérer ces propositions, il est évident que nous devrons nous donner des principes taxonomiques unificateurs, comme ceux que Lavoisier à inaugurés pour la chimie. Le système d'unités de base pour cette taxonomie, mériterait d'être révisé, en fonction des invariants relativistes et quantiques. L'ampère en particulier, non invariant relativiste, devrait être remplacé par l'unité de charge électrique. La constante de Planck, quantum d'action et de moment angulaire[5], doit elle aussi devenir unité de base, à usage taxonomique des grandeurs physiques.
Il faudra enfin se décider à donner un nom à l'unité macroscopique d'impulsion. Cela rendra enfin prononçables des raisonnements aussi élémentaires qu'indispensables. Je suggère "hamil", abréviation du fondateur de la mécanique symplectique. Il nous faudra aussi centrer en partie le système d'unités physiques sur le théorème de Noether, et sur la représentation symplectique.
Cela pose le mètre et le hamil sur un pied d'égalité, comme unités de grandeurs duales, de même symétrie, et conjuguées, aussi bien dans le théorème de Noether, que dans les relations de Heisenberg : 1 joule.seconde = 1 hamil.mètre = 1 unité macroscopique d'action. En physique, les produits intérieurs et contractés, ou produits scalaires, sont presque toujours exogamiques, soit entre grandeurs duales canoniques : impulsion par position, ce qui donne une action (dualité par l'action : si l'on choisit la position comme vecteur, alors l'impulsion est covecteur, et réciproquement); soit duales par l'énergie, comme impulsion par vitesse; ou encore duales par la puissance, comme l'intensité par la différence de potentiel. Alors qu'entre grandeurs homogènes, ou endogamiques, on ne trouve que des produits extérieurs : des vrais mètres multipliés par des vrais mètres, donnent de vrais mètres carrés; ou un rayon vecteur par un élément de courant, donne obligatoirement un produit extérieur : un champ magnétique, tenseur de rang deux.
L'oubli de la distinction entre produit intérieur et produit extérieur dans les monômes dimensionnels, est corrélatif à l'oubli du radian dans lesdits monômes dimensionnels. L'unité de moment d'un couple s'exprime plus brièvement, et plus clairement, comme joule par radian, que comme kg.m2.s-1, ou même que comme newton.mètre. Car après tout, dans l'esprit de nos étudiants, qu'est-ce qui différencie un newton.mètre d'un joule ? En tout cas rien de ce que mes collègues leur aient enseigné, à ce jour. Le radian n'est presque jamais perçu comme le quotient de deux longueurs perpendiculaires; or c'est ce qui explique que son carré soit égal à -1.
Examinons l'histoire et les conséquences de la confusion entre un espace réel de dimension 2, 3, ou 4, avec un complexifié ou un hypercomplexifié de R : j'ai nommé C, l'espace des complexes, et H, l'espace des quaternions.
Dans le plan réel (ou dans l'espace affine E3), toutes les directions sont réelles, et sont des directions de repères valides. Changer de base est facile et autorisé. Dans C, la direction réelle et la direction imaginaire (les directions imaginaires, pour H) sont tout sauf interchangeables. Sémantiquement, on cherche des renseignements sur une fonction à valeurs réelles, en la considérant comme la projection réelle d'une fonction complexe, ou hypercomplexe, ou comme le carré hermitien d'une fonction complexe. Si algébriquement, on a trouvé une ressemblance, cela n'ouvrait pas droit à l'assimilation pure et simple, comme on l'a fait.
Entre 1798 et 1843, des mathématiciens et des astronomes ont remarqué, ou inventé les choses suivantes :
L'addition des nombres complexes est isomorphe[6] à l'addition des vecteurs du plan.
Notamment, la partie réelle et la partie imaginaire d'un nombre complexe peuvent représenter les coordonnées d'un vecteur, sur deux axes orthonormés. Jusque là, il n'y a presque rien à redire aux exposés de Wessel et d'Argand. Si tout de même : Comment faites-vous pour changer d'axes sur le plan réel ? Rien de plus facile, et l'algèbre tensorielle convient à merveille. Et comment faites-vous pour changer d'axes sur le plan complexifié de la droite réelle ? Hem! algébriquement, on peut, mais la signification fiche le camp, et aucun garde-fou ne peut encadrer le débutant. Quel axe du plan est plus réel qu'un autre ?
Autre problème : la répugnance à s'apercevoir que dans tout problème physique ou pratique de la géométrie, les grandeurs qu'on considère, ne sont que rarement des nombres, mais des produits de nombres par des unités physiques. A cette époque, cette vérification élémentaire était encore plus incongrue. Les vecteurs d'un plan appartiennent à la catégorie des grandeurs : ils ont une unité physique, du genre longueur. Les nombres complexes n'ont pas d'unité physique. Isomorphisme certes, mais déjà la première disqualification.
La multiplication par 1 représente une identité.
La multiplication par un réel r, représente une homothétie centrée sur l'origine du repère.
La multiplication par i, représente un quart de tour (conventionnellement à gauche).
La multiplication par eiq, représente une rotation d'angle q, comptée dans le sens direct.
La multiplication par reiq, représente une rotation d'angle q, comptée dans le sens direct, suivie d'une homothétie de rapport r.
Donc maintenant, les vecteurs de base, sont réinterprétés ainsi :
1, comme pas de rotation du tout,
i, comme quart de tour à gauche, dans le plan.
Et la table de multiplication s'écrit :
|
. |
1 |
i |
|
1 |
1 |
i |
|
i |
i |
-1 |
Alors que la première interprétation résiste à un changement d'axes, par exemple par une rotation de 45°, la seconde interprétation est pulvérisée par une telle transformation. Un vecteur de base de C représente tantôt un vecteur de base, tantôt pas de rotation et tantôt un quart de tour à gauche. Un complexe représentait tantôt un vecteur et tantôt une rotation! Tantôt des mètres, et tantôt des radians!
Leur confusion perdure encore aujourd'hui, entre nombre et grandeur : un nombre complexe est un nombre. La multiplication de deux nombres est une opération interne. Un vecteur du plan est une grandeur. La multiplication de deux grandeurs, par exemple de deux vecteurs, est une opération externe. Mais les astronomes de l'époque ne sont pas avisés de cette contradiction sémantique. Leurs excuses : les nombres complexes en tant que substituts sténographiques des outils d'algèbre linéaire propres au plan, restent un puissant moyen de calcul pour la géométrie plane, et les fonctions analytiques sont fascinantes. Inversement, en électricité, où ce sont les nombres complexes qui sont compétents, on aime bien tracer des diagrammes de Fresnel, et diverses extensions spécialisées : diagrammes de Kapp pour les transformateurs, de Behn-Eschenburg pour les alternateurs, de Blondel pour les moteurs, etc.
Ainsi on a oublié d'élucider le mystère de la coïncidence entre le radian de la géométrie, qui est un quotient de deux longueurs égales et perpendiculaires, et le radian des phénomènes périodiques, qui est le quotient de deux grandeurs en quadrature de phase.
Transposant aux nombres complexes l'opération de produit scalaire, nous obtenons ceci :
Si z = reiq, et son
complexe conjugué
![]() =
re-iq, alors :
r2 =
=
re-iq, alors :
r2 =
![]()
D'où le produit hermitien :
![]() =
=
![]() =
=
![]()
Commençons par ne voir que le membre de droite. La partie réelle est bien l'image du produit scalaire : produit des modules, par le cosinus de l'angle. Autrement dit, produit contracté d'un vecteur, par la projection intérieure de l'autre vecteur.
La partie imaginaire est aussi l'image d'un produit, couramment appelé "vectoriel", et qui est encore moins vectoriel que le premier n'est scalaire. C'est le produit d'un vecteur par la projection extérieure de l'autre, et est donc l'aire algébrique de la surface du parallélogramme construit sur les deux vecteurs, orientée en rotation.
Brut, le produit hermitien est pertinent pour décrire un phénomène avec période et phase, là où les complexes sont compétents. Il est couramment utilisé en électrotechnique (sans, bien sûr, être nommé hermitien) : le produit de la tension par le courant, en alternatif, a pour partie réelle la puissance moyenne, ou puissance active, en watts. La partie imaginaire est la puissance réactive, en voltampères réactifs.
Mais pour gagner un début de compétence dans les
domaines vectoriel et dérivés, le produit hermitien
doit être symétrisé, il donne alors le produit
scalaire :
½(![]() +
+
![]() )
=
)
=
![]() .
.
Antisymétrisé, il donne aussi un résultat
intrinsèque : ½(![]() -
-
![]() )
= i
)
= i
![]() .
Mais la magie est alors moins éblouissante.
.
Mais la magie est alors moins éblouissante.
La petite tragédie eut son climax en 1843 : comme ses prédécesseurs, Hamilton (1805-1865) emmêla deux cahiers des charges incompatibles, quand il créa l'algèbre des quaternions.
Sémantiquement, il voulait créer les quotients des vecteurs de E3. Faire quelque chose d'isomorphe à l'addition des vecteurs de l'espace, était très simple. Il voulait obtenir l'outil algébrique quotient de deux vecteurs. Son cahier des charges sémantique, aurait dû n'aboutir qu'à l'algèbre tensorielle.
Comme ses prédécesseurs, Hamilton a complètement oublié l'indispensable algèbre des unités physiques.
Tout le drame est que fasciné par l'interprétation confusionniste des complexes, il a voulu prolonger ce confusionnisme dans l'espace de dimension 3, agrandir de même la multiplication et la division, et obtenir à nouveau un corps[7]. Il a donc agrandi la confusion entre nombres (complexifiés), et grandeurs physiques. Il s'est ainsi donné un cahier des charges structurel calqué sur les nombres complexes, autrement dit sur le complexifié de la droite réelle R, avec ce produit interne, dont l'interprétation géométrique plane emmêle les rotations dans les translations. Il a ainsi inventé en 1843, une très belle algèbre, de nombres hypercomplexes, qu'il a appelé les quaternions. Quater__ parce qu'à la recherche du groupe des rotations de E3 (espace affine à R3), il s'est retrouvé devant un corps de dimension quatre.
Puis il a appliqué naïvement ses hypercomplexes à l'espace physique réel (qu'il voyait en minkowskien avant la lettre). Les physiciens, dans leur majorité, ne se sont pas encore aperçus que cette confusion entre rotations et translations, où l'on fourre tout dans le même sac, tourne le dos à tout sens physique. Comme Wessel et Argand avant eux, les physiciens après Maxwell, se sont cramponnés à l'idée infantile que puisque le produit de deux nombres est encore un nombre, alors le produit de deux vecteurs devrait être encore un vecteur.
A sa mort, Christophe Colomb croyait toujours avoir découvert la route des Indes. A sa mort, Hamilton prenait toujours que ses quaternions pour ce qu'ils ne sont pas : un outil de calcul des transformation de l'espace E3. Il a fallu attendre en gros E. Cartan (1869-1951) et ses spineurs, et R. Penrose et ses twistors, pour que des mathématiciens prennent conscience (et eux seuls, hélas!) de ce qu'est la complexification d'un espace, et que ce n'est pas exactement la même chose que d'en augmenter le nombre de dimensions.
Dimension 4, donc quatre "vecteurs" de base, et non trois :
|
· Pas de rotation du tout (c'est le 1 des complexes ordinaires), · quart de tour en roulis (c'est le i des complexes ordinaires), · quart de tour en tangage (c'est un nouvel imaginaire pur, j), · quart de tour en lacet (c'est le troisième imaginaire pur, k).
|
|
Et la table de multiplication des quaternions s'écrit :
|
. |
1 |
i |
j |
k |
|
1 |
1 |
i |
j |
k |
|
i |
i |
-1 |
k |
-j |
|
j |
j |
-k |
-1 |
i |
|
k |
k |
j |
-i |
-1 |
Tout
quaternion non nul a un inverse : x .
![]() =
1, où
=
1, où
![]() est
le conjugué de x.
est
le conjugué de x.
Les produits croisés sont anticommutatifs : ij = -ji = k. jk = -kj = i. ki = -ik = j.
En tant qu'algèbre, c'est à dire espace pré-vectoriel de nombres, muni d'une seconde opération associative et distributive, notée multiplicativement, ceci reste irréprochable (et très fécond). Tout le drame vient de ce que Hamilton et les mathématiciens britanniques, ne savaient pas distinguer un nombre d'un grandeur, ni une longueur d'une surface ou d'un angle, ni un vecteur d'une suite de nombres sans règle ni syntaxe. Ils n'ont pas suspecté combien est malsaine l'évidence subliminale qu'une algèbre de nombres se permette de nous dicter subrepticement quelle serait donc la structure de l'espace géométrique de la physique... Les tout premiers soupçons britanniques n'arriveront qu'avec Clifford (1845-1879). Et seul Clerk Maxwell (1831-1879) pensera à la syntaxe des unités physiques, mais sans obtenir de résultats.
Ces produits de quaternions unitaires sont interprétables géométriquement selon ce double sens[8] :
Opérer une rotation I sur une rotation J, donne une rotation K;
Opérer une rotation I sur le vecteur j, donne le vecteur k,
et une rotation J sur le vecteur i, donne le vecteur -k.
Mais il n'a jamais été géométriquement justifié, que multiplier le vecteur i par le vecteur j donne l'objet mal identifié k. Et dans quelle unité ? En mètres ? en mètres carrés ? en radians ?
Et sur la diagonale, les choses prennent aussi une tournure bizarre :
Opérer une rotation I sur une rotation I, donne une rotation -1, ou demi tour; parfait.
Multiplier le vecteur i par le vecteur i donne -1. Bizarre pour un
vecteur, de générer l'opposé du produit
scalaire. Mais cohérent avec les complexes, que multiplier i
par
![]() ,
à la fois conjugué et inverse, donne 1.
,
à la fois conjugué et inverse, donne 1.
Mais pourquoi opérer une rotation I sur le vecteur i, donnerait l'objet mal identifié -1 ? En 1873, W. K. Clifford avait déjà souligné que le produit d'un vecteur par un quaternion non perpendiculaire, n'a aucun sens du tout (Clifford 1873). Signification impossible. Unité physique impossible aussi, évidemment.
Les symétries sont aussi alarmantes : les rotations et les vecteurs ont des comportements opposés.
C'est Hamilton qui a inventé le "vecteur" Ñ (quaternion imaginaire pur). Il lui a servi à dériver une force d'un potentiel. Stokes (1819-1903), et Tait (1831-1901) en ont étendu l'usage à la dérivation d'un champ de vecteurs (Stokes 1849, Tait 1867), produisant ce que Clerk Maxwell a proposé d'appeler convergence (opposé de la divergence) pour la partie scalaire, et (avec une grande défiance) rotation (rotationnel) pour la partie "vectorielle" (1873).
On voit qu'en dehors de leur beauté algébrique, les quaternions posent des problèmes d'interprétation insolubles, si on prétend les appliquer naïvement à la physique, comme l'ont fait Hamilton, Tait, et Macfarlane[9]. Gibbs et Heaviside avaient mille fois raison, quand ils objectaient à Tait, que les quaternions ne conviennent pas du tout à la physique. L'ennui, est qu'eux non plus n'ont pas mis dans le mille, et que presque personne - sauf Einstein, Weyl et Cartan - n'a rien fait après eux. Les quaternions appliqués façon 19e siècle, amalgament tout et n'importe quoi, et leur descendant direct, le produit "vectoriel", ne pouvait faire que pis encore.
Les mathématiciens ont admiré l'audace de Hamilton, et la beauté du corps des quaternions. Ils ont un peu rechigné : la multiplication n'était plus commutative. Ils ont dû vérifier que c'était inévitable. On a généralement oublié de remarquer, que la multiplication des quaternions, est généralement incompatible avec toute projection sur un sous-espace vectoriel. Ce qui est chose grave, pour un espace vectoriel. Les quaternions, comme tout système de nombres complexes ou hypercomplexes, ne sont que pré-vectoriels.
Un an plus tard, en 1844, Grassmann (1809-1877) publia l'outil mathématique approprié, avec notamment la première distinction ferme entre nombres et grandeurs (même si les grandeurs restent provisoirement abstraites, avant toute application physique, et sans unités). Mais voilà, Grassmann était un professeur peu connu, et son style philosophique kantien (aussi terrifiant que celui des Eléments d'Euclide) contrevenait aux habitudes des mathématiciens de l'époque, alors que Hamilton était un astronome déjà connu pour génial, ex-enfant prodige. Son formalisme canonique de la mécanique, de 1834, est toujours insurpassé. Hamilton a connu l'Ausdehnungslehre de Grassmann vers 1852, mais s'est surtout préoccupé à son sujet de calembours (mangeur d'herbe), et de questions d'antériorité.
Depuis ces dates, les physiciens jouent de malchance, et, sous couleur de simplifier (couleur qui leur sert à esquiver leurs tâches de clarification sémantique), ratent tous leurs rendez-vous avec leurs outils mathématiques corrects et appropriés[10], se contentant d'adorner d'habits neufs les vieilles confusions. Dans son traité de 1873, J. Clerk Maxwell (1831-1879) multiplie les mises en garde contre les impropriétés de sa mathématisation, ne s'y fiant qu'à demi. Les mots "vector product" ne se rencontrent que sous la plume de Clifford (1845-1879), en 1877. Tous deux ignoraient l'oeuvre de Grassmann jusqu'en 1878[11]. Visiblement, en 1894, les mises en garde de Clerk Maxwell étaient déjà oubliées[12], car Pierre Curie (1859-1906) prit soin de redémontrer en détail combien la représentation du champ magnétique par un vecteur, est impropre (Curie 1894). Peine perdue que celle de Curie : les physiciens perdirent de vue le modèle physique correct (dû à Ampère (1775-1836), Clerk Maxwell, W. Thomson (1824-1907), E. Weber (1804-1891), Pierre et Jacques Curie), parce que la mathématisation usuelle le contredisait. Et aussi parce qu'ils se débattaient alors dans une ignorance physique dont nous n'avons plus la moindre idée : l'électron n'a été inventé qu'entre 1891 et 1897, et prouvé en 1897; avant cela, Faraday (1791-1867), Clerk Maxwell, Poynting (1852-1914), Heaviside (1850-1925), etc. ont dû héroïquement bricoler des concepts inextricables pour imaginer la simple conduction électrique (et la charge électrique) : ici une vibration d'éther, là un vortex, ou une discontinuité des vecteurs déplacements, un croisement de vortex, une éponge de vortex, une contraction des tubes de forces, etc...
On peut constater au long des publications et manuels du siècle écoulé, que la faute de mathématisation, a éliminé le modèle physique correct (les courants ampériens), et consacré la conception erronée d'Œrsted (1777-1851), de Wollaston (1766-1828), de Faraday, etc. ("spectre de limaille facile implique vrai vecteur magnétique", voire "courant électrique invisible implique vortex"). Même Dirac (1902-1984) s'y est laissé prendre jusque vers 1970 [13]. Chaque fois que voir une grandeur physique orientée fut impossible, des physiciens furent déroutés, et beaucoup se sont égarés. Le prestige d'une mathématisation obscure a souvent suffi à éteindre leur perception kinésique. Nos élèves, eux, préfèrent dédaigner toute la physique, pour sa malmathématique embrouillée.
Les physiciens ont rejeté les quaternions de Hamilton, à cause de la dimension quatre. Mais pris par l'urgence, prêts à accepter n'importe quoi, qui leur permette des calculs, ils en ont gardé les confusions entre vecteurs et rotations, entre nombre et grandeur. Ignorant les bivecteurs de Grassmann, et se fiant à la foi quaternionienne de son ami Tait, Clerk Maxwell a tacitement utilisé le produit "vectoriel" extrait des quaternions. Ce produit "vectoriel", et cette confusion, rendirent incompréhensibles un tiers de l'électromagnétisme et de la mécanique, avec d'absurdes lois chirales et de travers. Maxwell était conscient du problème, sans avoir de solution[14], et il est mort à 48 ans. Inconscients, les autres ont ignoré les mises en garde de Maxwell.
Incompatible avec la définition des vecteurs comme classes d'équivalence de bipoints, et même avec les axiomes des espaces vectoriels, par exemple avec la projection sur un sous-espace vectoriel, le produit "vectoriel" a été extrait (par restriction, ou projection) du produit de quaternions imaginaires purs.
La table de multiplication INTERNE s'écrit ainsi :
|
X |
i |
i |
k |
|---|---|---|---|
|
i |
0 |
k |
-j |
|
j |
-k |
0 |
i |
|
k |
j |
-i |
0 |
Et elle se dessine de la même façon que pour les quaternions.
La grosse différence, est qu'il n'y a plus d'élément neutre, ni plus aucun inverse. Tandis qu'apparaissent des diviseurs de zéro. Le carré de tout "vecteur" est désormais nul : i x i = j x j = k x k = 0.
C'est ainsi que l'on perd l'associativité, qui était préservée en quaternions :
(i x j) x j = -i (même résultat qu'en quaternions), mais i x (j x j) = 0.
Cette perte de l'associativité contredit directement l'intention sémantique initiale : Tout ça c'est des vecteurs, ils se valent tous. Et leur ordre m'importe peu, il me suffit de changer le signe du résultat, quand je permute le multiplicateur et le multiplicande. La non-associativité prouve la contradiction interne. Retenons donc que, en syntaxe cohérente, l'ordre des termes ne sera jamais libre : le tourneur strict agit sur le vecteur.
Le produit "vectoriel" implique deux résultats joliment absurdes :
En physiciens, donnons une longueur concrète à nos vecteurs. Si les vecteurs i, j, k sont de longueur 1 mètre, alors k, qui est le produit de i par j, est de longueur 1 m². D'autre part, i et j sont de longueur 100 cm, donc k est de longueur 10 000 cm². D'autre part, j, produit de k par i, est alors de longueur 1 m3. Donc i, produit de j par k, est de longueur 1 m5, ou 1010 cm5. Etc... etc... Il n'y a aucune limite à l'absurdité.
D'autre part, rappelons-nous la définition des vecteurs comme classes d'équivalences de bipoints. Considérons donc ce trièdre, dans un miroir parallèle au plan xOz, i et k sont conservés par la symétrie, mais j est retourné, donc k, produit "vectoriel" de i par j, est retourné en -k. Donc k = -k. On peut recommencer sur les deux autres vecteurs de base, et on peut étendre par combinaison linéaire.
Ce qui démontre que la composante vectorielle, du produit "vectoriel", est identiquement nulle.
Nous avons donc démontré, par deux fois, que le produit "vectoriel" est une opération invalide.
C'est avec cette algèbre contradictoire avec elle-même, que les physiciens du 19e siècle, ont cru résoudre mathématiquement, le problème des tourneurs, dont ils avaient besoin, et dont on a toujours besoin.[15]
Cette construction, ayant tourné le dos à la géométrie et à la physique, garde les défauts des complexes et des quaternions naïfs : impuissants à respecter les unités physiques, et l'exigence de covariance des lois physiques. A la façon d'un dahut, qui ne tient debout que si tout est de travers, tout s'écroule au premier changement de repère non orthonormé. Incohérente avec les unités physique, et les vecteurs de base physiques, et incohérente avec les lois de la dérivation[16], cette construction confond les mètres avec les mètres carrés, et avec les angles, parce qu'elle refuse de distinguer les nombres des grandeurs. Physiquement, elle est désastreuse. Pédagogiquement, elle brave l'expérience, et le bon sens. Elle contredit et bafoue le cahier des charges de la physique. Le "vecteur" de physicien, jamais défini, a dévoré les lois de la dérivation.
Pour simplifier ? Il suffit d'écouter les conversations entre professeurs d'électrotechnique (qui sont la population-prétexte du pour simplifier), pour avoir la preuve que seules de longues années de dressage, leur permettent de ne plus s'embrouiller entre main droite et main gauche, aux trois doigts prétendus indispensables, l'une pour un moteur, l'autre pour un générateur (ou l'inverse ?). Pour simplifier! Quel gâchis!
Pour représenter simplement les quarts-de-tour, présents dans quelques lois de la physique, les moyens mathématiques corrects existent au complet depuis 1888 (Ricci-Curbastro 1888). En 1921, dans sa première conférence de Princeton (Einstein 1921), Einstein a montré à quel point ils sont pratiques, et pas plus difficiles que le jargon petit-nègre inscrit au programme officiel.
A condition d'être enfin complétée par l'algèbre des unités physiques, l'algèbre pertinente est l'algèbre tensorielle[17] : elle a exactement la bonne structure, isomorphe à la classe des phénomènes physiques élémentaires. Le plus souvent, il suffit de son sous-ensemble, l'algèbre extérieure, de Grassmann, Poincaré, et Cartan.
7.1.1.1. En premier, et depuis au moins 42 siècles, nous rencontrons l'usage littéral : est vecteur ce qui véhicule quelque chose. Par exemple une flèche incendiaire tirée depuis un arc à corde très lâche, fut un vecteur de combustion, capable de provoquer un incendie dans les fortifications en bois de l'adversaire.
7.1.1.2. En second, nous rencontrons sa mathématisation immédiate (mais correcte), pour les besoins de la physique : est vecteur ce qui caractérise une translation. Ce cahier des charges est rempli par la définition de Bellavitis : les vecteurs comme classes d'équivalences des bipoints par la relation d'équipollence. La sémantique précédente est donc conservée, dans ses grandes lignes, mais connaît une schématisation. Du point de vue mathématique, et dans le langage axiomatique que nous devons aux écoles de Klein et de Hilbert, nous avons besoin des axiomes des espaces vectoriels, plus une métrique, plus le moyen de définir une translation. Ce qui implique que l'espace en question soit au moins approximable localement par un espace affine pseudo-euclidien tangent. Du point de vue pratique, cela signifie que l'on peut valablement dessiner, et se servir de ses mains, d'une règle, d'un compas, d'une équerre, ou de ses pas, et de ses outils d'atelier, pour se guider dans les raisonnements.
Par extension légitime, est aussi considéré comme vecteur, tout ce qui dérive du vecteur de translation, par une dérivation ou intégration selon une variable qui n'est pas d'espace (le temps, notamment), ou par multiplication par une grandeur, dont la dimension physique ne comprend aucune longueur, à quelque puissance que ce soit.
7.1.1.3. En troisième lieu, nous rencontrons les éléments de tout espace vectoriel abstrait, quel qu'en soit la signification, ou le vide de sens, avec ou sans métrique.
En algèbre, on ne demande à un espace vectoriel abstrait, que d'être un groupe commutatif pour une opération, usuellement notée "+", et d'être stable pour une opération externe, appelée multiplication par les éléments d'un certain corps K, auquel aucune autre particularité n'est demandée que d'être un corps algébrique.
Toutefois, cela implique des propriétés, comme celles des projections sur des sous-espaces vectoriels, l'existence de bases, de la décomposition unique sur une base, et des lois de changement des coordonnées selon les changements de base, afin de conserver invariante une éventuelle signification. Très simples, ces lois n'ont été énoncées et comprises que très tard, et restent encore lettre morte pour la majorité des enseignants concernés. Nous suggérons de désigner par le terme "vectoroïdes" les éléments d'un espace vectoriel abstrait.
Et pourtant, dès les classes primaires, nos enfants rencontrent des espaces vectoriels, de dimension généralement 1 : les grandeurs physiques scalables.
7.1.2.1. Trois sans lois. C'est l'état sauvage et archaïque du second concept, venant du 19e siècle qui ne pratiquait que des coordonnées cartésiennes, et se méfiait de toute démarche géométrique intrinsèque. Par paresse mathématique, on ("on" : disciples maxwelliens, Heaviside) a édicté que tout ce qui n'est pas vecteur, et qui n'est pas vraiment nombre, est quand même vecteur. Notamment les rotations infinitésimales.
On s'est donc dispensé de toute espèce de définition qui soit mathématique - car quelle qu'elle soit, on la viole constamment (à chaque "produit vectoriel", notamment). On se contente d'avoir un usage, qui est en usage dans la peuplade. Pour eux, il suffit d'avoir une liste de nombres, appelées composantes, au lieu de coordonnées, sans aucune loi de changement de base, car on ne veut pas savoir changer de base. On tient bien à l'addition des vecteurs, et à la multiplication par un scalaire, mais on en refuse les conséquences inévitables, et se dispense des contraintes qui en découlent. On se permet le plus souvent d'être incohérent avec l'opération de projection sur un sous-espace vectoriel, et a fortiori, avec l'immersion dans un espace de dimension supérieure. Il arrive même qu'on se dispense de toute homogénéité dimensionnelle entre lesdites composantes.
Dans la suite, nous désignerons ce concept "laxeur", car il est caractérisé par son laxisme.
Techniquement, c'est un record, plus ou moins hétérogène. Sémantiquement, son intention est tantôt de désigner un vrai vecteur, tantôt le record homogène compacté d'un tenseur, d'un ordre non précisé (souvent un tenseur antisymétrique de rang 2), plus rarement un record hétérogène, représentant par exemple les trois constantes de l'équation d'une droite du plan : aX + bY + c = 0, voire quelque chose d'encore plus hétérogène.
7.1.2.2. N'importe quelle liste de nombres, Cet usage se rencontre en mécanique quantique : un vecteur d'état. On l'a aussi rencontré parfois en micro-informatique, où un vecteur n'était autre qu'un pointeur, vers une routine vitale, comme la routine d'initialisation à l'allumage, ou celle d'erreur mortelle.
Cette fois, il n'est même plus question d'addition ni de multiplication : une liste, rien d'autre.
On peut rencontrer des cas logiquement différents : la liste chaînée, de longueur a priori inconnue, le record structuré, mais dont la structure est mystérieusement connue et attendue par des moyens externes, et la suite, indexée sur un ensemble dénombrable. Les espaces de Banach reposent sur de telles suites, indexées sur un ensemble dénombrable, ou non.
7.1.2.3. N'importe quelle liste de nombres, structurée.
C'est ce qu'on appelle en informatique un RECORD.
Certains peuvent bien être, simple question de hasard, des coordonnées de vecteurs, d'autres sont des indicateurs booléens, ou des numéros d'un type logique énuméré, des numéros de méthode pour le programme qui va utiliser et interpréter ce RECORD. D'autres champs du record peuvent être occupés par tout autre chose que des nombres.
Simplement, dans un RECORD, il ne faut pas s'attendre à ce que la méthode d'utilisation des champs successifs, soit uniforme. Soit que chaque nature et chaque méthode est convenue d'avance, soit que chaque champ porte un drapeau qui signale sa nature, et le type de méthode qui sera compétent.
La sémantique diffère, donc la méthode de conception du programme, donc aussi la méthode de test, et le jeu de test seront qualitativement différents. Et en pédagogie, la stratégie didactique, comme les méthodes pédagogiques seront nécessairement distinctes, selon le type logique des champs du RECORD.
Par exemple, je peux très bien considérer 4,5 m.s-1 comme un record, composé d'un nombre "4,5", d'un exposant implicite "1" sur l'unité physique "mètre", d'un exposant "-1" sur l'unité physique "seconde", et d'exposants implicites "0" sur les autres unités fondamentales du système d'unité alors en usage. C'est du ressort de ma liberté individuelle. Toutefois, si je vous prétendais que ceci est un vecteur, de dimension au moins 3, vous me traiteriez immédiatement de farfelu, et vous auriez raison. Or, ce n'est ni plus ni moins farfelu que de traiter les 9 coordonnées d'un tenseur antisymétrique de rang 2, de "vecteur" en dimension 3... Là tout s'est passé comme si, en traitement algébrique de la géométrie, on n'avait pas encore conquis le chiffre zéro. Comme si, trois coordonnées nulles - dans quelques repères privilégiés seulement - c'était comme rien, ce qui autoriserait à un traitement elliptique et obscur.
|
|
Vecteur qui véhicule. |
Vrai vecteur géométrique et physique. |
Elément d'espace vectoriel abstrait. |
Trois sans lois. |
N'importe quelle liste de nombres. |
|
Nature des composants, ou "champs". |
|
Grandeurs physiques homogènes |
Nombres, ou non précisé. |
Grandeurs physiques. |
N'importe quoi. |
|
Sémantique |
Transport, comme sur un chariot |
Caractériser une translation |
Néant |
Contradictoire |
Néant |
|
Addition, multiplication par scalaire |
|
OK |
OK |
OK |
Néant |
|
Algèbre : règle de covariance |
|
OK |
OK |
Astuces d'évitement de l'obstacle |
Néant |
|
Cohérence avec sous-espaces, et sur-espaces |
|
OK |
OK |
Refusé |
Néant |
|
Symétries géométriques |
|
OK |
OK |
Contradictoire |
Néant |
|
Métrique |
|
OK |
Ajoutable |
Contradictoire |
? |
|
Physique : règles dimensionnelles |
|
OK |
Ignoré |
Parfois |
Néant |
|
Qui l'utilise ? |
Public cultivé, biologistes, militaires, etc. |
G. Bellavitis, H. Weyl, A. Einstein. |
Mathématiciens, certains physiciens théoriciens |
Physiciens, techniciens |
Des snobs ? |
|
Qui sait l'utiliser avec sécurité ? |
Public cultivé, biologistes, militaires, etc. |
Vous, demain |
Mathématiciens |
Certains d'entre les physiciens |
? |
|
Qui en a besoin ? |
Tout le monde : logistique, biologie. |
Tous physiciens, tous techniciens. |
Mathématiciens, physiciens |
Personne |
Nul n'a besoin de désigner une liste par un autre vocable que "liste". |
|
Désignation proposée : |
Vecteur |
Vecteur |
Vectoroïde |
Laxeur |
Liste |
Agrandissons la zone des trois-sans-lois, pour en mieux discerner le détail, et ses liens avec le voisinage :
|
|
Tenseur sur un espace vectoriel ou affine. |
Record homogène, compacté d'un tenseur. |
Record homogène |
Record hétérogène |
Liste |
|
Nature des composants, ou "champs". |
Nombres ou grandeurs physiques homogènes. |
En général des réels |
Tous des entiers, ou tous des réels. |
Nombres, champs logiques et énumérés. |
N'importe quoi. |
|
Sémantique |
Selon rang du tenseur. |
Empruntée à ce tenseur |
? ? ? |
A détailler selon la nature des champs. |
A découvrir sur place. |
|
Addition, multiplication par scalaire |
OK |
OK |
Probablement sans objet. |
Néant |
Néant |
|
Algèbre : règle de covariance |
OK |
A emprunter manuellement au tenseur signifié |
Probablement sans objet. |
Néant |
Néant |
|
Cohérence avec sous-espaces, et sur-espaces |
OK |
Impossible |
Impossible |
Contradictoire |
Néant |
|
Symétries géométriques |
OK |
Impossible |
Impossible |
Contradictoire |
Néant |
|
Métrique |
OK |
A emprunter manuellement au tenseur signifié |
? ? ? |
Contradictoire |
|
|
Physique : règles dimensionnelles |
OK |
Possible, mais hasardeux |
? ? ? |
Contradictoire |
Néant |
|
Qui l'utilise ? |
|
Physiciens, techniciens |
Mathématiciens |
|
|
|
Qui sait l'utiliser avec sécurité ? |
|
Certains d'entre les physiciens |
Mathématiciens |
|
|
|
Qui en a besoin ? |
Toute la Physique |
Personne |
Mathématiciens, physiciens |
|
|
|
Désignation proposée : |
Rang 1: vecteur, covecteur. Rang 2, antisymétrique : Tourneur Tenseur, sinon. |
Laxeur |
Record |
Record |
Liste |
Selon ce tableau, il faut considérer les six coordonnées du "Sechstervektor" qu'utilisait encore A. Einstein en 1916, et que Whittaker a utilisé jusqu'à la fin de sa vie ("Six-vector"), comme des records hétérogènes.
De même toutes les représentations usuelles des "torseurs", se caractérisent par leur hétérogénéité.
Prenons l'exemple d'un vecteur
![]() de
l'espace affine ordinaire :
de
l'espace affine ordinaire :
![]() =
Vi
=
Vi
![]() +
Vk
+
Vk
![]() +
Vl
+
Vl
![]() =
V1 e1 + V2 e2 +V3
e3 . Il est naturellement rapporté à
des vecteurs unitaires de base, qui sont eux-mêmes
rapportés
à une unité de longueur. Ces vecteurs unitaires sont
donc exprimés en mètres. Tandis que les
coordonnées
(contravariantes) de notre vecteur sur ce repère, ne sont que
des nombres.
=
V1 e1 + V2 e2 +V3
e3 . Il est naturellement rapporté à
des vecteurs unitaires de base, qui sont eux-mêmes
rapportés
à une unité de longueur. Ces vecteurs unitaires sont
donc exprimés en mètres. Tandis que les
coordonnées
(contravariantes) de notre vecteur sur ce repère, ne sont que
des nombres.
Les coordonnées du tenseur métrique g, sont
donc exprimées en mètres carrés, leur unité
naturelle. Les coordonnées du tenseur métrique
réciproque sont donc en m-2. Le covecteur inverse
de
![]() s'exprime
naturellement sur la base duale (contravariante), qui est en m-1
:
s'exprime
naturellement sur la base duale (contravariante), qui est en m-1
:
![]() .
.
![]() =
1.
=
1.
Il est devenu habituel de considérer sans précautions
une seconde expression possible : exprimer
![]() en
fonction de la base duale, et inversement, le vecteur dual en
fonction de la base directe. Mais alors les nouvelles
coordonnées
cessent aussitôt d'être des nombres sans dimension.
en
fonction de la base duale, et inversement, le vecteur dual en
fonction de la base directe. Mais alors les nouvelles
coordonnées
cessent aussitôt d'être des nombres sans dimension.
Sur la base duale (contravariante, en m-1), les
coordonnées (covariantes) de
![]() sont
en m2. Si l'on passe en unités cm, les
coordonnées
sont alors divisées par 100 : ce sont des cm2.
Tandis que les coordonnées naturelles (contravariantes) sont
multipliées par 100.
sont
en m2. Si l'on passe en unités cm, les
coordonnées
sont alors divisées par 100 : ce sont des cm2.
Tandis que les coordonnées naturelles (contravariantes) sont
multipliées par 100.
Résumons : 2 m = 2 ´ 1 m = 200 ´ 1 cm = 200 cm2 ´ 1 cm-1 = 2 m2 ´ 1 m-1.
Nous avons bien vérifié sur les coordonnées covariantes : 200 cm2 = 2 m2 /100.
Sur la base directe (en m), les coordonnées du dual de
![]() sont
en m-2. Si l'on passe en unités cm, les
coordonnées
sont alors multipliées par 100. Tandis que les
coordonnées
naturelles sont divisées par 100.
sont
en m-2. Si l'on passe en unités cm, les
coordonnées
sont alors multipliées par 100. Tandis que les
coordonnées
naturelles sont divisées par 100.
Résumons : 0,5 m-1 = 0,5 ´ 1 m-1 = 0,005 ´ 1 cm-1 = 0,005 cm-2 ´ 1 cm = 0,5 m-2 ´ 1 m.
Nous avons bien vérifié sur les coordonnées contravariantes : 0,005 cm-2 = 0,5 m-2 ´ 100.
Et pourtant, depuis Elie Cartan, tout le monde croyait malin de répéter ce barbarisme dimensionnel : "En repère orthogonal, la distinction entre composantes covariantes, et composantes contravariantes disparaît" (Cartan 1946). Autrement dit : 200 = 200 cm2. Et 5 = 5 cm-2. Ahurissant. Tout est prêt pour l'affirmation : "5 flacons = 5 pétroliers", ou pour le calcul de l'âge du capitaine en additionnant les oies avec les chèvres.
Nous avons rencontré jusqu'ici les garde-fous suivants :
Des garde-fous abstraits : la règle syntaxique de changement des coordonnées selon les changements de base. Les règles des symétries. Des règles de cohérence entre la signification prétendue, et la propriété algébrique d'associativité ou non. La cohérence des unités physiques, ou cohérence dimensionnelle.
Les garde-fous concrets : l'épreuve expérimentale. Y compris l'épreuve d'enseignement.
Un garde-fous sémantique, qui est d'abord pratique, et social ensuite. Le codage d'allure mathématique (donc intimidant pour beaucoup), devient bien plus sûr, et devient vraiment vérifiable, si on a accepté d'en écrire préalablement la signification expérimentale, en langage clair, accessible au plus grand nombre. Il est si facile de se tromper seul. Il est si facile de tromper la poignée d'élèves dociles qui dépendent de votre bon plaisir pour obtenir son examen final. Si vous supprimez tout repère sémantique, vous restreignez outrageusement le public capable de vous relire, de comprendre vos erreurs, et de vous corriger. Et vous supprimez du même coup la plupart des critères qui permettraient de repérer ce qui correct, et ce qui s'est égaré.
Si le lecteur accepte de se souvenir du modeste début de ses brillantes études, il devrait se souvenir qu'à l'aide de figures de ce genre, son instituteur lui a appris qu'on obtient la surface d'un rectangle, en multipliant la longueur d'un côté par la longueur d'un côté adjacent.
|
|
Commençant par travailler sur des entiers et des longueurs entières, vous avez été invités à constater que "multiplier" un segment de longueur 4 par un segment perpendiculaire de longueur 7, dans la même unité, produit bien une surface rectangulaire, d'aire 28 carreaux carrés. Chaque carreau unitaire ayant l'unité de longueur pour côté.
|
L'énoncé restait très prudent et rigoureux : "multiplier le nombre qui mesure la longueur par le nombre qui mesure... etc.", évitant d'introduire des ambiguïtés entre {segment : ensemble de points} et {longueur : grandeur} (en dimension 1), et entre {surface : ensemble de points} et {aire : grandeur} (en dimension 2).
Peu d'années après, vous avez appris à ramener le calcul de l'aire d'un parallélogramme à celle d'un rectangle. Par une opération qu'on omettait de désigner[18], on obtenait la hauteur du parallélogramme; sur cette hauteur et la base, on construisait un rectangle, puis on multipliait la mesure de la base par la mesure de la hauteur, et on obtenait la mesure de l'aire du rectangle; et par le jeu de deux triangles isométriques (on disait : "égaux"), on montrait que cette mesure était aussi celle de l'aire du parallélogramme.
|
|
Les triangles BCC' et ADD' sont égaux. Le rectangle ABC'D' a même aire que le parallélogramme ABCD. Pourvus de procédures sur les mesures des aires, on n'avait pas explicité de moyen d'appréhender ces grandeurs indépendamment d'une unité de mesure. |
Vous avez pratiqué le produit cartésien, y compris le produit R ´ R associé au plan. Vous avez caractérisé les translations, obtenant ainsi des vecteurs. Vous aviez en mains tous les composants, prêts à servir. La progression logique eût été que le prochain pas fût d'enchaîner sur le produit extérieur des vecteurs, obtenant ainsi l'aire orientée du parallélogramme. Mais personne n'a pratiqué la progression logique.
A partir de la terminale, vous avez appris deux produits, un "produit scalaire" et un "produit vectoriel". Conformément à l'infirmité de l'école anglaise de Hamilton (1805-1865) et de Cayley (1821-1895), qui ne parvenait pas à bien discerner un vecteur d'une liste de nombres (pouvant être éventuellement des coordonnées de vecteur) sans structure ni règle, ces produits vous ont été enseignés comme des résultats de calculs sur coordonnées, au lieu d'une définition intrinsèque, dont on eût vérifié la cohérence mathématique (notamment géométrique). Cela donnait quelque chose du genre : pour obtenir le "produit scalaire" vous additionnez les produits de composantes deux à deux [19]. Pour le "produit vectoriel", c'est un vecteur dont on obtient les composantes par telle différence de produits croisés. Les repères étant tacitement toujours orthonormés.
A ce stade-là, le praxéogramme[20] des concepts emmagasinés dans votre cursus scolaire, a l'allure dispersée suivante :
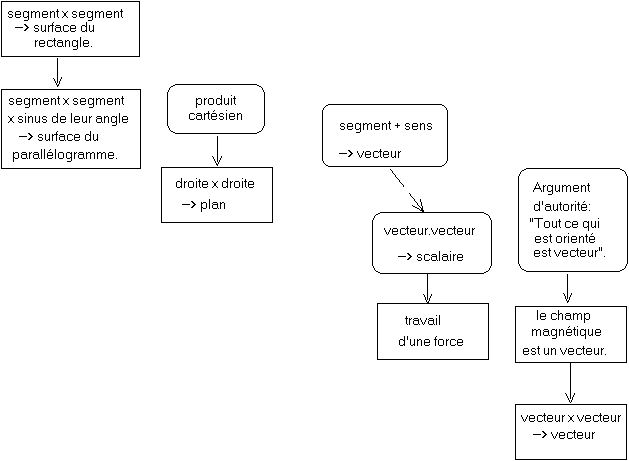
|
|
Notamment, on vous a fait apprendre (donc approuver) des affirmations de ce genre : «Le vecteur unitaire k est le produit vectoriel du vecteur i par le vecteur j, unitaires.» Or comme chacun de ces vecteurs est de dimension unitaire, soit physiquement un mètre, le vecteur k est en même temps de longueur un mètre carré. Ce qui est une propriété fort surprenante pour un vecteur unitaire dans un repère orthonormé : 1 m = 1 m². Et tout ce qui s'ensuit : 1 m = 1 m2 = 1 m3 = 1 m-1, etc. Et comme, implicitement, un vecteur ne serait qu'une liste de (trois) nombres, et que 1 m = 100 cm, alors 100 = 10 000 = 1 000 000 = 0,01, etc. |
Et s'il n'y avait que cette contradiction là!... Evidemment, vous n'y aviez vu que du feu, alors. Ainsi va la physique de concours, avec son ultimatum habituel : approuvez à l'instant, ou partez.
Aujourd'hui, quitte à faire un effort d'honnêteté, vous devriez vous souvenir de votre stupéfaction, la première fois que vous avez vu le professeur sortir de sa manche la mystérieuse troisième direction, dans laquelle il a mystérieusement choisi un sens pour y placer son mystérieux troisième vecteur. Rappelez-vous : vous n'avez commencé à y "croire" un peu, que lorsqu'on vous a donné l'exemple d'applications en magnétisme. Comme par hasard : il est impossible de voir un champ magnétique, alors qu'on peut voir tourner une vitesse angulaire et un moment angulaire. Aussi fallait-il commencer par vous mettre sous dépendance en magnétisme, avant de vous asséner le produit vectoriel en mécanique, toute vigilance anesthésiée.
Les professeurs de mathématiques, qui réticents, enseignaient quand même cette absurdité, parce qu'elle est au programme, faisaient passivement confiance : "il paraît que ça sert en physique", et renonçaient à comprendre pourquoi[21]. Sans se douter qu'il n'y avait rien à comprendre, et tout à refaire.
Si vous avez appris l'algèbre extérieure et l'algèbre tensorielle, notamment pour survoler les leçons sur la Relativité, vous avez repris la progression logique commencée à l'école primaire, là où on vous avait forcé à la discontinuer et délaisser. De nouveau, on vous a autorisé à distinguer un nombre d'une grandeur.
|
|
Le rectangle ABC'D' a même aire orientée que le parallélogramme ABCD. "Orientation" signifie ici sens de parcours du périmètre : parcourir d'abord le segment AB, puis le segment BC. Cette aire orientée est l'opposée de celle du parallélogramme ADCB. |
Mais trop souvent, au lieu de vous donner les heures de travaux dirigés nécessaires pour maîtriser le calcul extérieur, et ses applications physiques, le professeur a biffé tout son travail, d'une contradiction : «ceci signifie le produit vectoriel»[22]. Conclusion pragmatique de cette contradiction : oublier la cohérence logique, oublier l'algèbre extérieure, garder le "produit vectoriel", qu'emploie la puissante majorité. Vous n'avez guère gardé en mémoire que la règle de changement de base. En oubliant de s'en servir pour vérifications de cohérence. En oubliant comment se servir en pratique des règles de covariance et de contravariance.
On remarque un domaine cohérent à gauche, mais écartelé par de longues années d'inaction dans le cursus scolaire : l'algèbre linéaire est totalement cohérente avec la géométrie.
Séparé et incompatible, un domaine purement autoritaire à droite, autour du "produit vectoriel", qui domine le gros des physiciens et des électrotechniciens. Un domaine intermédiaire (semi-correct) entre les deux, où le produit scalaire hésite à être intérieur ou scalaire ou scalable, et où scalaire est tacitement non-défini.
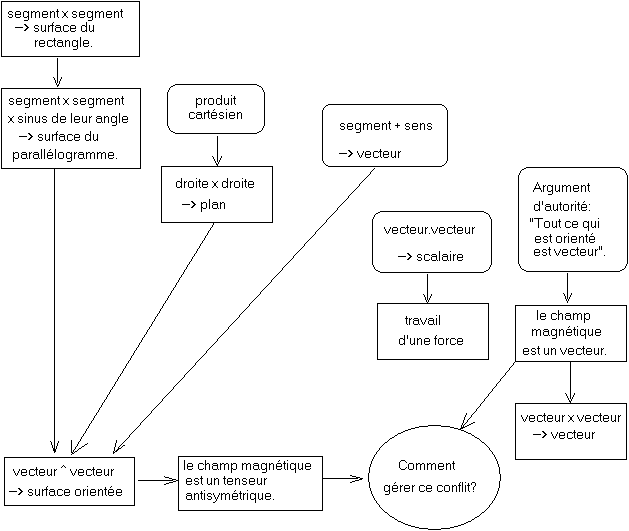
Les mauvaises relations entre métiers ont fait que personne ne s'est soucié de restituer une cohérence décente dans les systèmes de concepts enseignés de ci de là.
Une minorité de lecteurs bâille d'ennui : elle sait déjà que le champ magnétique, le flux magnétique, le moment angulaire, le moment d'une force, la vitesse angulaire, l'accélération angulaire, la vitesse aréolaire, et quelques autres grandeurs, de symétrie similaire, sont des tenseurs antisymétriques de rang deux.
Des quoi ? grommelle la majorité, au bord de l'insurrection. Elle n'a pas tout à fait tort. Donnons donc un synonyme bref et clair; qualifions-les de tourneurs.
Oui, le mot est déjà pris, et utilisé dans les ateliers. "Tourneur", et son dérivé "grandeur tornatorielle", désignent désormais les grandeurs physiques qui prennent un vecteur d'une espèce, le projettent dans un plan stable, et lui font faire un quart de tour dans ce plan stable, pour engendrer un certain autre vecteur.
L'opérateur de projection est appelé "projecteur" par les mathématiciens depuis longtemps. Ce mot est connu des physiciens quantiques. L'opérateur de rotation n'a pas encore reçu de baptême bref qui fasse l'unanimité. "Rotateur" est utilisé en anatomie, et en chimie organique (lumière polarisée), et je suggère de le réutiliser. Le tourneur est le composé d'un projecteur orthogonal sur un plan, et d'un rotateur d'un quart de tour dans le même plan stable. Ces opérateurs commutent : ils ont même plan stable.
La minorité citée plus haut proteste à son tour : «On n'a pas besoin de tourneurs, on disait déjà "vecteur axial"» (variante : "pseudovecteur"[23]). "Vecteur", disiez-vous ? C'est pourquoi vos collègues comprenaient toujours vecteur, tout court. La nuance "pseudo", ou "axial"[24], était invariablement perdue et incomprise par vos contemporains moins instruits. D'ailleurs, même chez ceux qui la prononçaient, la nuance "axiale" restait lettre morte dès qu'ils calculaient, car eux aussi se servaient d'un "produit vectoriel", dont ils devaient ensuite corriger à la main les fautes de symétries. Voilà pourquoi l'auteur considère les nuances "pseudo" et "axial" comme disqualifiées. Aucune nuance ne peut racheter le "produit vectoriel". Aucune habitude ancrée ne peut racheter le fait qu'on se trompe de mathématisation depuis 1843. Nos grands ancêtres avaient des excuses, nous pas; et les meilleurs d'entre eux nous avaient prévenus de leurs doutes.
Nos tourneurs, inventés par Grassmann, ont déjà été baptisés "bivecteurs" par E. Cartan. Le terme n'a pas eu grand succès, ni sa généralisation en multivecteurs, ou en p-vecteurs. Je devine deux raisons à cet insuccès : leur obscurité, et la collision avec les "quadrivecteurs" relativistes, utilisés dans l'espace de Minkowski. L'obscurité reste un défaut grave : comment feront les gens simples, pour deviner que "bivecteur" veut dire "être-de-rotation", tels une vitesse angulaire, un champ magnétique, ou une surface orientée en rotation ? "Bivecteur" ne se rapporte à aucun verbe d'action. Or le verbe d'action est indispensable aux gens simples.[25]
Et un tourneur, cela se dessine comment ? Comme un sens de rotation dans un plan. Efficacité ? Environ cinq secondes à froid, pour trouver le sens de rotation d'un moteur à courant continu. Dix secondes pour trouver le sens de la f.é.m. dans une dynamo. Trois secondes pour dessiner le sens d'un rotationnel. Dix minutes pour faire dessiner la pression de radiation d'une onde électromagnétique, à des terminales B.E.P. C'est vous dire...
Un langage d'experts tend à réduire le désordre des langues naturelles à d'honnêtes bijections : un mot par concept, un concept par mot. On vient de voir par quelques exemples, que dans leur état présent, la physique et la mathématique sont encore loin d'être des langages d'experts, mais sont bien aussi bordéliques que des langues naturelles. Les hasards contingents de l'Histoire, pleine de crimes et de fureurs, qui ont généré des coutumes, mathématique par exemple, ont laissé un paysage d'un illogisme opaque. Par étourderie conservatrice, on a hypostasié ce bric à brac, et on a ainsi bafoué, et l'ergonomie (sauf parfois l'ergonomie des matheux chevronnés, ou celle des astronomes du 19e siècle, mais jamais celle des débutants), et la sécurité. Chaque groupuscule, chaque suzerain local, a des prétentions à considérer le restant de l'espèce comme autant de sous-hommes, contre lesquels l'arme de son incivisme serait légitime, et imbu de sa juste idiosyncrasie, s'arroge le privilège d'ignorer les collisions sémantiques avec les autres professions utilisatrices des mêmes mots.
J'ai ici proposé de nouveaux morphèmes pour les concepts indispensables à distinguer : vecteur, vectoroïde, tourneur, pré-vecteur. J'espère voir disparaître ce que j'ai dû baptiser "laxeurs" : ils ne produisent que des dégâts dans l'entendement de nos élèves, ralentissent l'apprentissage, et gênent le recrutement de physiciens doués d'un esprit concret, logique, et libre.
Je préconise qu'on ose se servir bien davantage des concepts d'héritage et de classes, et du concept de grammaire; tous trois empruntés au génie logiciel. Toute la physique gagnerait à accueillir l'idée même de discipline et de syntaxe. Alors que présentement, trop de physiciens réagissent à la prononciation de ces deux mots, comme s'il s'agissait de menaces, ou d'insultes personnelles.
Il est utile d'emprunter aux psychiatres le concept d'épreuve de réalité. L'épreuve de réalité expérimentale des physiciens, a visiblement été calquée sur les cadrans de nos appareils de mesure, restreinte aux seules parties numériques des résultats; tandis qu'on occultait que les pseudo-outils utilisés prédisaient systématiquement des contre-vérités; ainsi les "produits vectoriels" prédisaient des symétries toujours fausses; l'oubli du radian dans les monômes dimensionnels entassait des grandeurs incompatibles dans la même case dimensionnelle; la confusion entre nombres et grandeurs conduisait tout droit au style âge du capitaine, où les calculs sont devinés par quelque "méthode globale", sans règles ni garde-fous. Devant le spectacle d'une épreuve de réalité ainsi carencée, je préconise qu'on emprunte aux professions voisines, clientes et fournisseuses, ou parallèles, leurs épreuves de réalité, leurs disciplines, leurs critères de pertinence. Nous n'en aurons pas trop!
Enfin, je préconise qu'on établisse entre nous des relations rationalisées de clients et de fournisseurs, et que nous mettions en place une politique de qualité, et les moyens de la qualité, avec des cahiers des charges explicites, et le management orienté qualité. Jusqu'à présent, ces mots-là ont été accueillis comme des gros mots.
Autant de mauvaises habitudes qu'on n'a pu garder qu'en secteur protégé, en monopole financé par l'impôt, où chaque suzerain local cumulait les rôles de juge et partie, de producteur monopoliste et contrôleur monopoliste, narguant aussi bien la fureur de ses clients, que la frustration de ses étudiants et de ses vassaux. Dans le secteur concurrentiel, toute entreprise payée par des clients libres, librement concurrencée par d'anciens employés envolés de leurs propres ailes, et qui se serait repliée sur ces vices-là, ferait faillite.
Barbotte J. 1948. Le calcul tensoriel. Paris, Bordas.
Benveniste E. 1975. Le vocabulaire des institutions indo-européennes. Tome 1. Paris, Editions de Minuit.
Bunge M. [1973. Philosophy of Physics. Doordrecht, Reidel]1975; Philosophie de la physique. Paris, Seuil.
Cartan E. 1946. Leçons sur la géométrie des espaces de Riemann. Paris, Gauthier-Villars [Réed. Gabay, 1988 Paris].
- [1937. Leçons sur la théorie des spineurs. Paris].1981; The Theory of Spinors. New York, Dover Pub.
Clerk Maxwell J. 1873, 2nde édition 1881. Treatise on Electricity and Magnetism. Réédition Dover Pub.
- 1877. Matter and Motion. 1920 : Society for Promoting Christian knowledge. 1991 : New-York, Dover Pub.
Clifford, W.K. 1873. Preliminary Sketch of Biquaternions. Mathematical Papers. Réed. Chelsea. New York. 1968.
- 1877. Notes of Lectures on Quaternions. Mathematical Papers.
- 1878. Applications of Grassmann's Extensive Algebra. Mathematical Papers.
Cohen-Tannoudji C., Diu B., Laloë F. 1977. Mécanique Quantique. Paris, Hermann.
Curie P. 1894. Sur la symétrie des phénomènes physiques. Journal de Physique, 3e série, t. III, PARIS 1894. Réimprimé dans : Oeuvres de Pierre Curie. Paris 1984, Editions des Archives Contemporaines.
Dahan-Dalmedico A. & Peiffer J. 1986. Une histoire des mathématiques. Routes et dédales. Paris, Seuil.
Einstein, A. 1916. Eine neue formale Deutung der Maxwellschen Feldgleichungen der Elektrodynamik. Prüss. Akad. Gesamsitzung. 3 feb. 1916.
- 1921. Quatre conférences sur la théorie de la relativité. Gauthier-Villars. Paris 1971.
Grassmann, H. G.. Die Lineale Ausdehnungslehre. 1ère édition en 1844, édition refondue en 1862. Traduction française par D. Flament : La science de la grandeur extensive. Lib. A. Blanchard. 1994 PARIS.
Hamilton W. R. 1853. Lectures on Quaternions; Dublin; in Mathematical Papers. Cambridge Univ. Press.
Hulin M. 1975. Quelques considérations élémentaires relatives aux "raisons de symétrie". Paris, Bull. Union Phys. n° 572 : 651 - 658.
Laloë F. 1984. Quel usage les physiciens font-ils de la mécanique quantique ? in Fundamenta Scientiae, Vol 5, n. 1, page 27.
Lounis A. 1990. Considérations historiques et difficultés d'élèves à propos des grandeurs vectorielles. Paris, Bull. Union Phys. n° 721 : 205 - 219.
Perrier P. 1975. Le premier monopôle magnétique ? La Recherche n° 61 : 965 - 966.
Ricci-Curbastro G. 1888. Delle derivazione covariante e contravariante. Padova.
Saint-Venant, Barré (de) 1845. "Mémoire sur les sommes et différences géométriques et sur leur usage pour simplifier la Mécanique", note à l'Académie des Sciences, septembre 1845.
Serrero M. 1969. La physique sans calculs. Paris, Bull. Union Phys. n° 518 : 17-24.
Stokes, Sir George G. 1849. Dynamical Theory of Diffraction. [Camb. Phil. Trans. 1849].
Tait, Peter G. 1867. Elementary Treatise on Quaternions. Oxford 1867, 1873, 1890.
Varenne J. 1979. Grammaire du sanskrit. Paris, QSJ-PUF.
Whittaker, Sir E. 1951. A History of the Theory of Æther & Electricity. Réed. New York 1989, Dover Pub.
Weyl H. 1921. Raum-Zeit-Materie. [Trad. Space-Time-Matter. Réed. New-York, Dover Pub. 1952].
Un oubli dans la bibliographie :
APMEP, Commission Mots, n° 6 : Grandeurs et mesures. APMEP, 1982, Paris.
| Ils ont mathématisé de travers, format pdf | Ils ont mathématisé de travers, format html |
[1] An 1844 plus 151 ans font 1995, date de rédaction de cet article.
[2] Ainsi, Franck Laloë a plusieurs fois vanté la justesse du viol de la rigueur par les physiciens : Quel usage les physiciens font-ils de la mécanique quantique? in Fundamenta Scientiae, Vol 5, n. 1, page 27,
ou dans les 4 premières pages du chapitre II, Les outils mathématiques de la Mécanique Quantique, dans : Cohen-Tannoudji, Diu, Laloë (1977) : Mécanique Quantique. Paris, Hermann.
[3] en astronomie : se dit d'une inégalité des mouvements de la lune, liée au déplacement du périgée et aux variations de l'excentricité.
[4] Composante : projection sur un axe du repère; elle est donc encore un vecteur de même nature. La coordonnée est la mesure algébrique de cette composante, soit le quotient de la composante, par le vecteur unitaire de cet axe. La coordonnée naturelle est donc un simple nombre. Les choses se compliquent quand on veut rapporter d'autres grandeurs physiques vectorielles, sur les mêmes vecteurs de base; par exemple, les coordonnées d'une quantité de mouvement (kg.m/s), projetée sur une base de longueurs, seront exprimées en kilogrammes par seconde.
[5] Planck h, ou Dirac hbar, c'est la même constante, mais exprimée dans deux unités d'angle différentes, le radian, et le tour : h = hbar = 6,6260755 . 10-34 joule.seconde/cycle = 1,05457266 . 10-34 joule.seconde/radian.
[6] Isomorphes : qui ont les mêmes propriétés algébriques.
[7] En algèbre, on appelle corps un ensemble doté de deux lois de composition internes, et qui est un groupe commutatif pour la première. Privé de l'élément neutre de la première loi, il est aussi un groupe pour la seconde loi, qui de plus est distributive sur la première loi.
Un groupe est un ensemble sur lequel on a défini une loi de composition interne associative, présentant un élément neutre, et dont tout élément possède un inverse.
[8] Ceci est l'interprétation historique : à une rotation d'angle q, on associe le quaternion unitaire, ou verseur, d'angle q. Il existe une réinterprétation moderne, qui associe au verseur d'angle q, la rotation d'angle 2q.
[9] Pire : ils ont prétendu représenter les tenseurs symétriques, tels que la perméabilité d'un diélectrique anisotrope, par une combinaison de quaternions.
[10] Ratant par exemple Barré de Saint-Venant (1797-1886) : "Mémoire sur les sommes et différences géométriques et sur leur usage pour simplifier la Mécanique", note à l'Académie des Sciences, septembre 1845.
[11] Clifford a publié en 1878 ses Applications of Grassmann's extensive Algebra, venant juste de découvrir l'Ausdehnungslehre.
[12] Dans son Matter and Motion, de 1877, Maxwell avait déjà oublié ses réserves, et présentait une règle chirale pour représenter un moment angulaire.
[13] En 1975, P. A. M. Dirac a désavoué sa précédente croyance en des monopôles magnétiques, à la déception de Price, qui croyait en avoir observé un ( Perrier 1975).
[14] Quand on étudie le traité de 1873 de Maxwell, on s'aperçoit qu'il était bien au courant de l'existence de grandeurs tensorielles du second ordre, comme les susceptibilités magnétique (introduite par S. D. Poisson en 1824, et démontrée symétrique par W. Thomson en 1851), ou diélectrique, anisotropes, et autres grandeurs à neuf composantes. Mais il était convaincu de leur symétrie en physique : l'effet Hall n'a été découvert qu'en 1880, un an après la mort de Maxwell. Il semble n'avoir jamais envisagé de tenseur ni de matrice antisymétrique. Dommage!
Il fut par ailleurs l'inventeur de la méthode photoélastique d'analyse des contraintes, à l'âge de 19 ans.
[15] Au 20e siècle, on mettra des habits neufs à la vieille confusion, avec une "dualité" de physiciens, "de Hodge", en eijk, incompatible avec la dualité des algébristes, et toujours violant la covariance des lois physiques.
[16] d'où ces cas de "double produit vectoriel" qu'on nous a asséné durant nos études, qui dissimulent presque toujours un calcul sur forme différentielle extérieure.
[17] Hélas, certains auteurs de manuels n'exhibent leurs connaissances tensorielles que comme signes extérieurs de culture, puis continuent leurs livres avec des produits "vectoriels", et des chapelets de "par analogie, ... par analogie ..."
[18] Nous détaillerons cette projection orthogonale extérieure. C'est indispensable.
[19] Il est indispensable que nous détaillons ultérieurement la projection orthogonale intérieure et le produit intérieur.
[20] Praxéogramme : graphe des actions, composant en séquence une action plus complexe. Exemple : une recette.
[21] Exception méritoire: Jean Barbotte; Le calcul tensoriel. Bordas, 1948. Paris.
Barbotte mentionne le livre de L. Brillouin, mais n'imite pas ses renoncements diplomatiques.
[22] Un exemple parmi tant d'autres : A. Dahan-Dalmedico & J. Peiffer. 1986. Une histoire des mathématiques. Routes et dédales. Page 286, 4e ligne, édition de poche Point. Paris. Seuil.
[23] Plus caustique, Michel Hulin écrivait : "vecteur de mauvaise foi". B.U.P. n°572. PARIS, 1975
[24] Attention aux choix des mots! Ces grandeurs "axiales" n'ont justement pas d'axe, mais un plan stable.
[25] J. W. Gibbs avait proposé le terme de dyadic, qui n'a pas percolé jusqu'aux physiciens de langue française.